Занятие № 10. Иррациональные уравнения и неравенства.
(Иррациональные уравнения.)
План.
- Понятие иррационального уравнения. Формулы, применяемые для решения иррациональных уравнений.
- Иррациональные уравнения и методы их решения.
Понятие иррационального уравнения. Формулы, применяемые для решения иррациональных уравнений.
Определение. Иррациональными называются уравнения, в которых переменные или рациональные функции находятся под знаком корня или возводится в дробную степень.
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
L Что значит решить иррациональные уравнения?
Это значит: найти все такие значения переменной х, при которых уравнение превращается в верное равенство, либо доказать, что таких значений не существует.
Обычный способ их решения сводится к освобождению от корней. Следует помнить, что корни четной степени выражения А(х) не существуют, если А(х) меньше нуля.
При решении задач необходимо пользоваться следующими эквивалентными преобразованиями: для уравнений
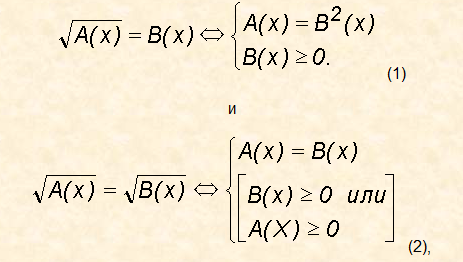
Широко распространенными иррациональными уравнениями, являются уравнения вида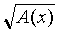 
= В(х), где А(х) и В(х) – алгебраические выражения, где неизвестная величина содержится под знаком корня и уравнения вида 
.
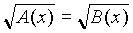E Вернемся к уравнению вида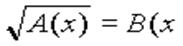 
:
Показывается способ решения уравнения данного вида:
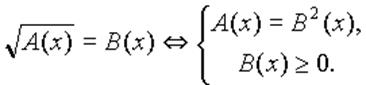(1)
Примеры:
1) 
;
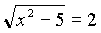2) 
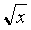= х – 2.
Обратите внимательно на правые части уравнений. Во втором уравнении должно налагаться дополнительное условие, которое вытекает из определения арифметического корня n -ой степени.
Имеем 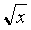= х – 2. Пришли к системе
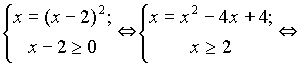
х 2– 5 х + 4 = 0
х 1 = 4,
х 2 = 1– посторонний корень, не удовлетворяет условию х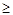 
2.
При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.
Еще один вид иррационального уравнения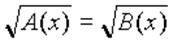 
сводится к системе
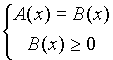(2)
Кстати, можно проверять и А(х) 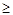0, т.е. то, что в данной задаче проще. Если уравнение не относится ни к одному из видов, то с помощью различных преобразований можно привести уравнения к I или II виду.
Иррациональные уравнения и методы их решения.
Основные методы решения иррациональных уравнений
I. УЕДИНЕНИЕ РАДИКАЛА И ВОЗВЕДЕНИЕ В СТЕПЕНЬ.
Пример 1. Решить уравнение: 
.
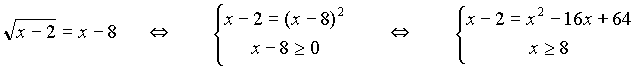
Рассмотрим уравнение системы х 2– 17 х + 66 = 0
х 1 = 11,
х 2 = 6 – пост. корень, т.к. х 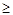8.
Пример 2. Решить уравнение: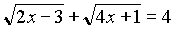 
Данное уравнение равносильно системе: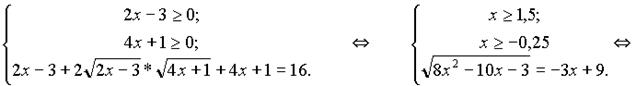 
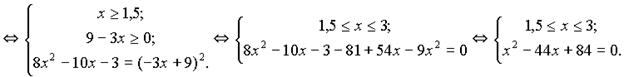
Решимуравнение системы: x 2 – 44 x + 84 = 0
x1= 2,
x2 = 42 - посторонний корень.
Ответ: x = 2
Пример 3.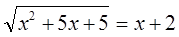 
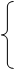Решение:
х2+5х+5=(х+2)2, 
х2+5х+5= х2+4х+4, х = -1,
х+2≥0, х≥-2, х ≥ -2.
Ответ: х=-1.
Пример 4.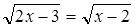 
Решение:
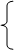
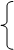2х-3=х-2, х=1,
2х-3≥0, х≥1,5.
Ответ: решений нет.
Пример 5.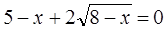 
.
Решение:
Преобразуем уравнение: 
.
Полученное уравнение равносильно смешанной системе:
.
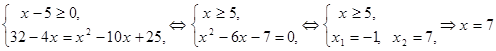Ответ: x = 7.
Пример 6.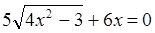 
.
Решение:
Преобразуем уравнение: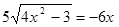 
.
Полученное уравнение равносильно смешанной системе:
.
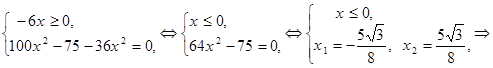
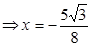Ответ: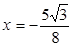 
.
Пример 7.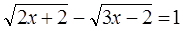 
.
Решение:
Область допустимых значений: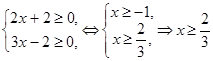 
.
Преобразуем уравнение: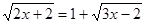 
. Возведем обе части этого уравнения в квадрат: 
, 
.
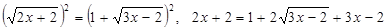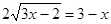Полученное уравнение равносильно смешанной системе:
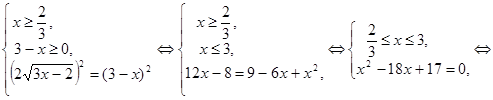
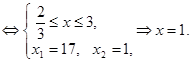
Ответ: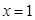 
.
Пример 8.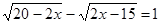 
Решение:
Область допустимых значений:
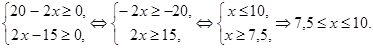
Преобразуем уравнение: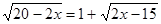 
. Возведем обе части этого уравнения в квадрат: 
,
.
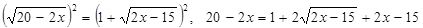Полученное уравнение равносильно смешанной системе:
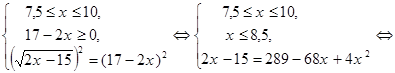
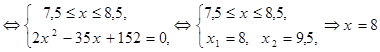
Ответ: x = 8.
Пример 9.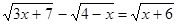 
.
Решение:
Найдем область допустимых значений (см. рис. 1):
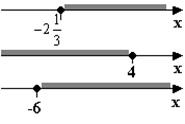
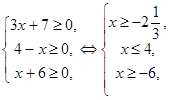
Рис. 1
Областью допустимых значений промежуток: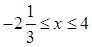 
или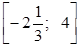 
.
Преобразуем уравнение: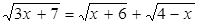 
.
Возведем обе части полученного уравнения в квадрат:
,
.
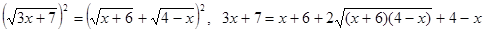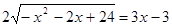Это уравнение равносильно смешанной системе:
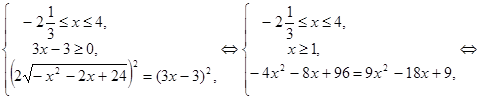
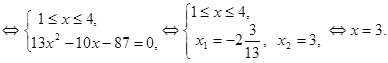
Ответ: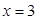 
.
Пример 10.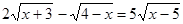 
.
Решение:
Найдем область допустимых значений (см. рис. 2):
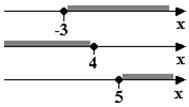
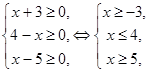
Рис. 2
Областью допустимых значений является пустое множество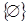 
, значит, уравнение не имеет решений.
Ответ: решений нет.
II. МЕТОД ВВЕДЕНИЯ ВСПОМОГАТЕЛЬНОГО НЕИЗВЕСТНОГО ИЛИ “МЕТОД ЗАМЕНЫ”.
Пример 1. Решите уравнение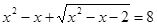 
.
Решение:
Пусть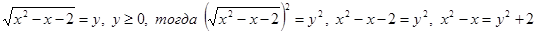 
,
Получим смешанную систему:
.
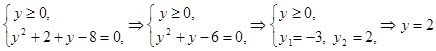Делаем обратную подстановку, получим:
.
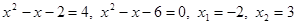Ответ: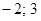 
.
Пример 2. Решите уравнение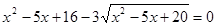 
.
Решение:
Пусть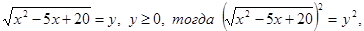 
,
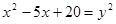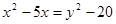, получим систему:
.
.
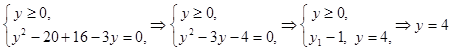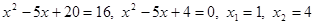Ответ: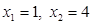 
.
Пример 3. Решите уравнение x 2 + 3 x – 18 + 4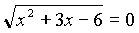 
Решение:
x 2 + 3 x – 6 – 12 + 4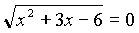
Пусть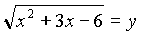 
, у = 0.
Получим новое уравнение: у 2 – 12 + 4 у = 0
у 2 + 4 у – 12 = 0.
у 1=– 6 (пост. корень, т. к. у =0)
у 2=2.
Вернёмся к подстановке: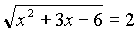 
. Данное уравнение дорешаем дома.
Пример 4. Решите уравнение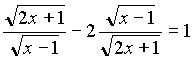 
Решение:
ОДЗ: (1;+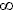 
)
Пусть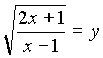 
, y >0.
Получим уравнение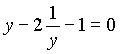 
,
y 2– y – 2 = 0.
у 1 = –1 – посторонний корень, т.к. у >0,
у 2 = 2.
Возвращаемся к подстановке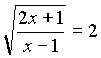 
x = 2,5. Уравнение дорешать дома.
Часто этот метод встречается при решении других уравнений, не только иррациональных.
Пример 5. Решите уравнение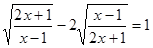 
.
Решение:
Выражения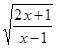 
и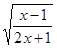 
являются взаимно обратными, если они не равны нулю, т. е. 
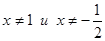, т. е. область допустимых значений:
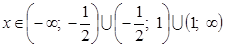
В самом деле: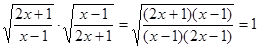 
.
Пусть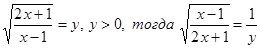 
, получим смешанную систему:
.
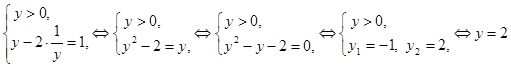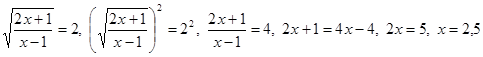- этот значение переменной входит в область допустимых значений и является корнем уравнения.
Ответ: x = 2,5.
III. УРАВНЕНИЯ, СОДЕРЖАЩИЕ КУБИЧЕСКИЕ РАДИКАЛЫ.
Пример 1. Решить уравнение: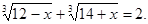 
Решение:
Положим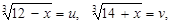 
тогда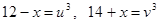 
.
Складывая левые и правые части этих равенств, получаем: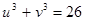 
.
Из данного уравнения, находим: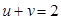 
.
Получим систему уравнений:
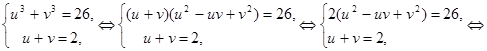
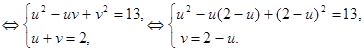
Решим первое уравнение системы:
.
.
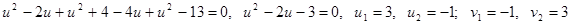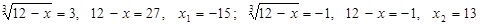Проверка
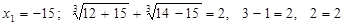, значит,
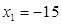- удовлетворяет уравнению.
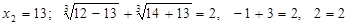, значит,
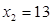- удовлетворяет уравнению.
Ответ: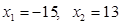 
.
Пример 2. Решить уравнение: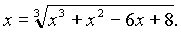 
Решение:
х – любое число, следует из свойства корня при n нечётном.
x 3 = x 3 + x 2– 6 x + 8
x 2– 6 x + 8 = 0
x1 = 2,
x2 = 4.
Ответ: x1 = 2, x2 = 4.
Основным методом решения таких уравнений является последовательное возведение в куб обеих частей уравнения, используя формулы
(а + в)3=а3 + в3 + 3ав(а + в)
(а– в)3 = а3– в3– 3ав(а– в).
Пример 3. Решите уравнение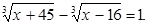 
Решение:
ОДЗ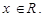 
Положим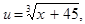 
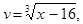тогда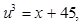 
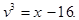
Подставляя в уравнение u и v, получим u - v = 1, а вычитая из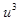 
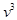, чтобы уничтожились x, получим уравнение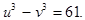 
В результате приходим к алгебраической системе уравнений с двумя неизвестными
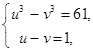
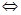
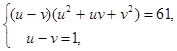
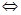
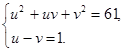
Выразим из второго уравнения u и подставим в первое уравнение, получим:
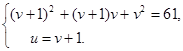
Решим первое уравнение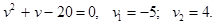 
Получаем два значения x: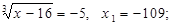 
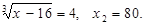
Проверка
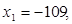
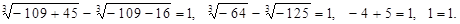
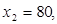
Ответ: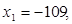 
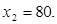
IV. “ИСКУССТВО” ИЛИ НЕСТАНДАРТНЫЙ ПОДХОД.
Пример 1. Решите уравнение Пример: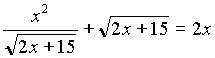 
.
Решение:
Разделим обе части уравнения на х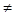 
0, получим уравнение 
.
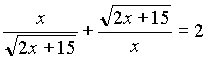Пусть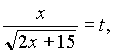 
тогда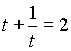 
.
t 2– 2 t + 1 = 0,
где t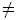 
0, (t – 1)2 = 0, t = 1. Уравнение дорешать дома.
Пример 2. Попробуйте решить:
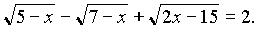
Решение:
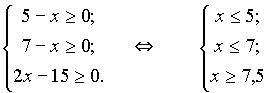
Ответ: нет решения.
Пример 3. Решите уравнение: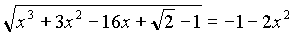 
По определению левая часть неотрицательное число, а (–1– 2х2 < 0), поэтому уравнение не имеет решения.
Ответ: нет решения.