И бесконечно большие функции (б.б.ф.).
Определение 7. Функции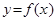 
и 
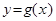называются эквивалентными (
~ 
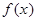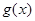) при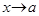 
, если 
.
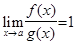Определение 8. Функция называется бесконечно малой функцией (б.м.ф.) при , если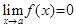 
. Функция 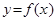называется бесконечно большой функцией (б.б.ф.) при 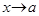, если 
.
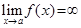Теорема. При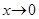 
справедлива следующая цепочка эквивалентных б.м.ф.: x ~ 
~ 
~ 
~ 
~ 
~ 
.
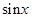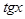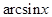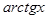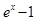Лемма. Если при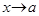 
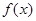– б.б.ф., то 
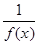– б.м.ф. Наоборот, если при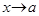 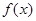– б.м.ф., то 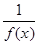– б.б.ф.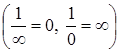 
Теорема. При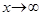 
справедлива следующая эквивалентность многочлена своей старшей степени: 
~ 
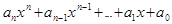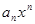, где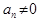 
.
Теорема. Если при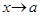 
~ 
и 
~ 
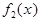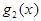, то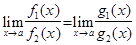 
, в случае, когда один из этих пределов существует.
Теорема.
1) Если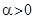 
, то 
, 
; если же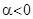 
, то 
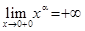, а 
.
2) Если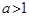 
, то 
, 
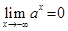; если же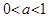 
, то 
, а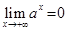 
. В частности, 
, 
.
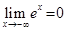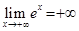3) Если 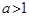, то 
, 
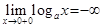; если же 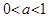, то 
, а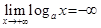 
. В частности, 
, 
.
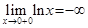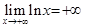4) 
.
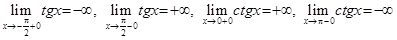5) 
.
6) 
.
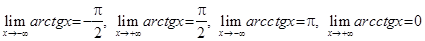Справедливы следующие соотношения (здесь c – ненулевая константа):
 ,  .
|
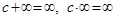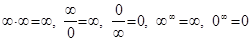Неопределенностями будем называть выражения вида:
|
Непрерывные функции
Определение 9. Функция 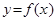называется непрерывной в точке 
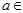D(y), если 
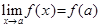. Иначе функция 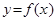называется разрывной в точке a.
Определение 10. Функция 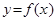называется непрерывной на множестве 
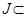D(y), если она непрерывна в каждой точке этого множества.
Свойства непрерывных функций
1. Постоянная функция непрерывна.
2. Сумма двух непрерывных функций непрерывна.
3. Произведение непрерывной функции на число есть непрерывная функция.
4. Произведение двух непрерывных функций непрерывно.
5. Частное двух непрерывных функций непрерывно в точках, в которых знаменатель неравен нулю.
6. Сложная функция, состоящая из двух непрерывных функций, непрерывна.
Все элементарные функции непрерывны на своих областях определения.
Асимптоты графика функции.
Пусть даны функция 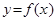, прямая 
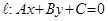, точка 
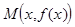на графике функции 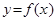и обозначим через 
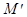проекцию точки M на прямую 
.
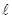Определение 11. Прямая 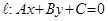называется левосторонней (соответственно, правосторонней) асимптотой графика функции 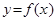в точке 
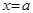(a может принимать и бесконечные значения), если при 
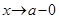(соотв. при 
) 
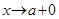, а 
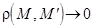(где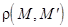 
– расстояние между точками M и ).
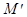Теорема. Прямая 
(здесь a – конечное число) является левосторонней (соотв., правосторонней) асимптотой графика функции 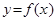в точке 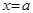тогда и только тогда, когда 
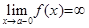(соотв, 
).
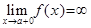Асимптоты вида называют вертикальными асимптотами.
График функции, непрерывной на всей числовой прямой, не имеет вертикальных асимптот.
Теорема. 1)Если прямая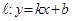 
является левосторонней (соотв., правосторонней) асимптотой графика функции 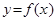на бесконечности, то
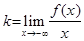
| (соотв.,  )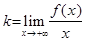
| ||
| (соотв.,  ).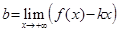
|
2) Если пределы данные выше пределы существуют и конечны, то прямая 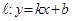является левосторонней (соотв., правосторонней) асимптотой графика функции 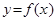на бесконечности.
Асимптоты вида 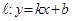называют наклонными асимптотами. В частности, если 
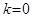, то такие асимптоты называют горизонтальными.
Теорема. Пусть 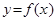– рациональная дробь, то есть
,
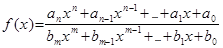где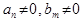 
, причем числитель и знаменатель не имеют одинаковых действительных корней. Тогда:
1) если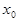 
– действительный корень знаменателя дроби, то 
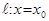– вертикальная асимптота графика функции ;
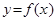2) график функции 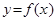имеет наклонные асимптоты тогда и только тогда, когда 
; при этом наклонные асимптоты в точках 
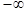и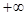 
совпадают.