Для определения моментов mk случайной величины X нужно вычислить k-ю производную от характеристической функции по параметру и и положить u = 0:
При исследованиях, связанных с совместным изучением нескольких случайных величин, кроме моментов каждой из них в отдельности, пользуются смешанными моментами случайных величин. Так, например, в случае системы двух случайных величин (X, Y) начальный момент (k1 + k2)- гo порядка определяется как математическое ожидание величины 
:
При k1=0 или k2=0 формула (3.33) дает моменты случайных величин X и Y по отдельности.
В табл. 3.2 приведены формулы для определения различных моментов двумерных случайных величин дискретного и непрерывного типов.
Среди смешанных моментов случайных величин особую роль играет центральный смешанный момент второго порядка m, который обычно называется корреляционным моментом (иначе «моментом связи», ковариацией) случайных величин X, Y и обозначается символом Kxy
Для дискретных случайных величин
где pij= p(X = x, Y = yj), а для непрерывных
Корреляционный момент Кху представляет собой такую характеристику системы случайных величин, которая описывает, помимо рассеивания величин X и Υ, еще и связь между ними. Часто вместо корреляционного момента Кху пользуются безразмерной величиной, называемой коэффициентом корреляции Rxy:
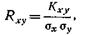(3.37)
Коэффициент корреляции Rxy удовлетворяет условию
-1£ Rxy £1 (3.38)
и определяет линейную вероятностную зависимость между случайными величинами.
Если X и Υ независимы, то К.ху = 0 и Rxy = 0. Две случайные величины, для которых коэффициент корреляции равен нулю, называются некоррелированными. Независимые величины всегда не коррелированы. Зависимые величины могут быть как коррелированными, так и некоррелированными. Для нормальных случайных величин некоррелированность означает также и независимость.
В некоторых случаях используются условные моменты случайной величины X относительно Υ. Для условных математического ожидания и дисперсии случайной величины X относительно Y формулы соответственно имеют вид
При решении задач настоящей главы следует иметь в виду известные соотношения для основных числовых характеристик случайных величин:
1) если С – не случайная величина, то
М(С) = С, М(СХ) = СМ(Х); (3.41)
2) для любых случайных величин X и Υ
Μ(Χ±Υ) = Μ (Χ) ±Μ(Υ); (3.42)
3) математическое ожидание линейной функции равно
где ai, b – не случайные коэффициенты;
4) для любых X и Υ
Μ (ΧΥ) = Μ (Χ) Μ (Υ) + Kxr (3.44)
Если Χ и Υ некоррелированы (Кху = 0), то
Μ (ΧΥ) = Μ (Χ) Μ (Υ); (3.45)
5) если С – не случайная величина, то
D(C) = 0;
6) не случайную величину С можно выносить за знак дисперсии, возводя ее в квадрат:
D(CX) = C2D(X), о(СХ) = |С|s(Х); (3.46)
7) для любых случайных величин Χ κ Υ
D(X±Y) = D(X) + D (Y) ± 2Kxr (3.47)
Дисперсия суммы (разности) некоррелированных случайных величин (К.ху = 0) равна сумме их дисперсий:
D(X±Y) = D(X) + D(Y); (3.48)
η
8) дисперсия линейной функции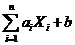 
определяется
формулой
Если все величины Χ1 Χ2,..., Хп не коррелированы, то
9) для независимых случайных величин X и У дисперсия их произведения равна
3.2. Задачи и ответы
3.2.1. Какие размерности имеют математическое ожидание т, дисперсия σ2 и среднее квадратичное отклонение σ?
3.2.2.Закон распределения дискретной случайной величины задан рядом распределения
Найти математическое ожидание тх и дисперсию σx2 случайной величины X.
Ответ: тх = 2; σx2 = 4,8.
3.2.3. Определить математическое ожидание тх и дисперсию σx2 числа приборов X, давших отказ за время испытаний на надежность, если испытанию подвергается один прибор, а вероятность его отказа равна q.
Ответ: mx = q; σx2=q(1 - q).
3.2.4. Стрельба ведется по наблюдаемой цели. Вероятность попадания при одном выстреле равна 0,5 и от выстрела к выстрелу не меняется.
Вычислить математическое ожидание тх и дисперсию σx2 случайной величины X – числа попаданий в цель при пяти выстрелах.
Ответ: тх = 2,5; σx2=1,25.
3.2.5. На вход ограничителя воздействует видеоимпульс со случайной амплитудой. Вероятность превышения импульсом уровня ограничения равна р.
Рассматривая событие превышения уровня ограничения импульсом как случайную величину X, принимающую значения 1 (превышение) и 0 (не превышение), определить среднее значение и дисперсию величины X. Найти среднее значение и дисперсию числа Υ импульсов, превысивших порог, при подаче на вход ограничителя η импульсов.
Ответ: тх = р, σx2= p(1–p); ту = пр, σy2 = пр(1–р).
3.2.6. Вероятность приема позывного сигнала одной радиостанции другой радиостанцией равна 0,2 при каждой посылке. Позывные передаются каждые 5 сек до тех пор, пока не будет получен ответный сигнал. Общее время прохождения позывного и ответного сигналов равно 16 сек.
Найти среднее число переданных позывных сигналов до установления двухсторонней связи.
Ответ:: т = 8.
3.2.7. В партии из 100 изделий имеется 20 бракованных. Из партии выбираются для контроля 5 изделий.
Определить математическое ожидание и дисперсию числа бракованных изделий, содержащихся в случайной выборке.
Ответ:m = 1; σ2 = 76/99.
3.2.8. Вероятность отыскания малоразмерного объекта в заданном районе в каждом вылете равна р.
Определить математическое ожидание и дисперсию числа произведенных независимых вылетов, которые выполняются до первого обнаружения цели.
Ответ: тх = 1/p; σx2= (1-p)/p2 .
3.2.9. Производится стрельба по цели до получения k попаданий. Вероятность попадания при каждом выстреле равна р. Случайная величина X – число необходимых выстрелов.
Найти математическое ожидание и дисперсию величины X.
Ответ: тх =k/p; σx2= k(1-p)/p2
3.2.10. В партии из η изделий имеется одно бракованное. Чтобы его обнаружить, выбирают наугад одно изделие за другим и каждое вынутое изделие проверяют.
Найти математическое ожидание тх и дисперсию σ* числа проверенных изделий.
Ответ: тх =k/p σx2 = k(1-p)/p2
3.2.11. Связь с дрейфующей станцией могут поддерживать η радиостанций. Вступает в двухстороннюю связь та из них, которая первой примет позывной дрейфующей станции, причем это событие
равновероятно для всех n радиостанций (р =1). Дрейфующая станция будет устанавливать связь т раз.
Определить: а) вероятность Ρ того, что радиостанция № 1 вступит в двухстороннюю связь k раз; б) математическое ожидание тх и дисперсию σx2 числа вступлений в двухстороннюю связь этой радиостанции.
Ответ:
3.2.12. Найти математическое ожидание тх и дисперсию σx2 случайной величины X, распределенной по закону Пуассона:
Ответ: тх =l; σx2=l.
3.2.13. Число вызовов на телефонной станции за единицу времени распределено по закону Пуассона. Математическое ожидание числа вызовов за час равно 30.
Найти вероятность того, что за минуту поступит не менее двух вызовов.
Ответ: 0,09.
3.2.14. На радиомаяк-ответчик в среднем поступает 15 запросов за 1 час.
Считая число запросов случайной величиной, распределенной по закону Пуассона, определить вероятность того, что за 4 мин: а) поступит ровно 3 запроса; б) поступит хотя бы один запрос.
Ответ: а) 0,0613; б) 0,632.
3.2.15. Радиостанция передает информацию в течение времени t= 10 мксек. Работа ее происходит при наличии хаотической импульсной помехи, среднее число импульсов которой в одну секунду составляет 104. Для срыва передачи достаточно попадания одного импульса помехи в период работы станции.
Считая, что число импульсов помехи, попадающих в данный интервал времени, распределено по закону Пуассона, найти вероятность Ρ срыва передачи информации.
Ответ [13]: Р = P(k > 0,τ). = 0,09516.
3.2.16. Случайная величина X принимает только целые неотрицательные значения с вероятностями
где
Определить математическое ожидание и дисперсию величины X. Ответ: тх=λ; σx2 = λ(1 +αλ).
3.2.17. Изменение частоты X генератора из-за самопрогрева подчинено распределению, график которого изображен на рис. 3.2.
Рис. 3.2. Плотность вероятности.
Определить: а) выражения для плотности вероятности W1(х) и функции распределения F1(x); б) математическое ожидание тх и среднее квадратичное значение случайной величины X.
Ответ:
3.2.18. Сообщение передается квантованными импульсами с шагом квантования Δ = 1в.
Предполагая, что ошибка квантования равномерно распределена в пределах интервала квантования и имеет нулевое среднее значение, определить дисперсию σ2 (мощность) шума квантования.
Ответ: σ2=1/12 В2
3.2. 19. Случайная величина X с математическим ожиданием тх = 4 и дисперсией σx2 = 3 распределена равномерно.
Найти плотность вероятности W1(x) величины X.
Ответ:
3.2.20. При измерении напряжения гармонического колебания u(t) =A sin (wt -φ)
ламповым вольтметром, проградуированным в эффективных значениях, стрелка вольтметра из-за наличия помех равномерно колеблется между значениями a1 и a2.
Вычислить: а) среднее значение т aпоказаний вольтметра; б) относительную погрешность Δ=s/т aизмерения амплитуды напряжения u(t), где σa – среднее квадратичное значение.
Ответ:
3.2.21. Время безотказной работы самолетного радиоэлектронного оборудования в полете является случайной величиной, распределенной по экспоненциальному закону.
Определить вероятность безотказной работы оборудования в течение десятичасового полета, если среднее время безотказной работы по статистическим данным составляет 200 час.
Ответ: 0,951.
3.2.22. Вероятность того, что станок, работающий в момент t0, не остановится до момента t a+ t, определяется формулой
P(t) = е-at
Найти математическое ожидание и дисперсию рабочего периода станка (время между двумя последовательными остановками).
Ответ:
3.2.23. Линия связи длиной l обслуживается ремонтной бригадой, база которой находится у середины линии.
Найти среднее значение и дисперсию расстояния (вдоль линии) от базы до места очередного ремонта, если известно, что последнее с одинаковой вероятностью находится в любой точке линии.
Ответ:
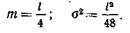
3.2.24. Точка брошена наудачу внутрь круга радиуса R. Вероятность попадания точки в любую область, расположенную внутри круга, пропорциональна площади области.
Определить математическое ожидание и дисперсию расстояния X точки до центра круга.
Ответ:
3.2.25. Радиотехническая система состоит из пяти последовательно соединенных устройств, среднее время безотказной работы каждого из которых составляет: Т1= 40, Т2 = 60, Т3 = 100, T4 = 80, Т5 = 150 час. Распределение времени безотказной работы устройств экспоненциальное.
Вычислить: а) среднее время Т0 безотказной работы системы; б) вероятность Ρ безотказной работы системы за время t = 3час.
Ответ: а) Т0 = 14,1 час; б) Ρ =0,811.
3.2.26. Плотность вероятности случайной величины X имеет вид
Определить математическое ожидание тх и дисперсию sх2 величины X.
Ответ: mx=σx2=m+1.
3.2.27. Плотность вероятности случайной величины X задана выражением
Найти математическое ожидание и дисперсию величины X.
Ответ:
3.2.28. Мгновенные значения амплитуды X принимаемого сигнала при замираниях описываются распределением Релея
Определить среднее значение и дисперсию случайной величины X.
Ответ:
3.2.29. Случайная величина R (расстояние от точки попадания до центра мишени) распределена по закону вида
Найти: а) коэффициент А; б) моду М, медиану Me, математическое ожидание тr и дисперсию σr2, величины R; в) вероятность Ρ того, что в результате выстрела расстояние от точки попадания до центра мишени окажется меньше его моды.
Ответ:
3.2.30. Интенсивность отказов элемента λ(t) определяется функцией вида
Определить: а) вероятность Ρ безотказной работы элемента в интервале времени 0 –10 час; б) среднее время Т0 безотказной работы элемента; в) плотность вероятности W1(t) распределения времени безотказной работы элемента.
3.2.31. Ряд распределения случайной величины X имеет вид
Вычислить математическое ожидание и дисперсию случайной величины Y = 1 - 2Хг.
Ответ: mу= - 2,4; σy2 = 9,63.
3.2.32. Доказать, что математическое ожидание центрированной и нормированной случайной величины
равно нулю, а дисперсия – единице.
3.2.33. Математическое ожидание и дисперсия случайной величины X равны соответственно mх и σx2.
Найти математическое ожидание и дисперсию случайной величины Υ = - X.
Ответ: ту= - тх; σy2 = σx2 .
3.2.34. Через равные временные интервалы произведено 36 измерений величины тока, при которых получены следующие результаты:
Определить среднее значение тока mi, среднее значение мощности М(I2) на единичном сопротивлении и дисперсию σi2.
Ответ: mi =10 мА; М(I2) = 104,5 мА2; σi2 = 4,5 мА2 .
3.2.35. Плотность вероятности случайной величины X задана выражением
Определить математическое ожидание и дисперсию случайной величины Υ = ЗХ -1.
Ответ: ту = 3; σy2 = 2..
3.2.36. Случайная величина Φ равномерно распределена в интервале от 0 до 2я.
Вычислить математическое ожидание и дисперсию величины A0 cos2 (ω0t + Φ), где А0, ω0, t – неслучайные величины.
Ответ:
3.2.37. Случайная величина К дискретного типа распределена по закону Пуассона
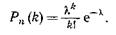
Показать, что первые моменты этого распределения вероятностей выражаются следующими формулами:
mi = μ2 = μ3 = λ; μ4 = λ (1 + 3λ).
3.2.38. Доказать справедливость следующего соотношения между центральными μk и начальными mk моментами:
3.2.39. Случайная величина X имеет плотность вероятности вида
(экспоненциальный односторонний закон).
Определить: а) функцию распределения F1(x); б) математическое ожидание т, дисперсию σ2, коэффициенты асимметрии γ4 и эксцесса γ2.
Ответ:
3.2.40. Показать, что для распределения Лапласа
справедливы следующие формулы для моментов случайной величины X:
3.2.41. Найти центральные μk и центральные абсолютные nk моменты случайной величины X, распределенной по нормальному закону
Ответ: При k – нечетном μk = 0,
При k – четном
3.2.42. Показать, что для одностороннего нормального распределения
среднее значение и дисперсия соответственно равны
а начальный момент k- гoпорядка определяется формулой
3.2.43. Найти для бета-распределения, задаваемого плотностью вероятности
начальный момент k- гoпорядка.
Ответ:
3.2.44. Определить характеристическую функцию θ1(и) случайной величины X, принимающей: а) одно единственное значение, равное с; б) с одинаковой вероятностью два значения, равные ±с.
Ответ: а) θ1(и)=еjuc; б) θ1(и) = cos(uc).
3.2.45. Вероятность появления события А при одном испытании равна р.
Найти характеристическую функцию θ1(и) числа появлений события А при одном испытании.
Ответ: θ1(и) = 1 + p (еju -1).
3.2.46. Доказать, что для биномиального закона распределения вероятностей
характеристическая функция θ1(и) имеет вид
3.2.47. Характеристическая функция случайной величины К равна
Показать, что К является дискретной случайной величиной с равномерным законом распределения вероятностей:
3.2.48. Найти характеристическую функцию θ1(и) случайной величины, подчиненной закону Пуассона с параметром λ:
Ответ:
3.2.49. Плотность вероятности W1(x) случайной величины X представляет собой четную функцию.
Доказать, что характеристическая функция θ1(и) величины X. вещественна.
3.2.50. Показать, что если 
– характеристическая функция случайной величины X, то плотность вероятности w(x) этой величины равна
3.2.51. Найти плотности вероятности случайных величин, имеющих следующие характеристические функции:
Ответ:
3.2.52. Показать, что характеристической функции
соответствует плотность вероятности
3.2.53. Определить характеристическую функцию θι(«) случайной величины X, плотность вероятности которой равна
Ответ:
3.2.54. Случайная величина X имеет плотность вероятности
Вычислить характеристическую функцию величины X.
Ответ:
3.2.55. Определить характеристическую функцию θ1y(и) случайной величины Υ = аХ + b, где а и b – постоянные.
Ответ:
3.2.56. Доказать, что, характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.
3.2.57. Показать, что если случайные величины X и Υ связаны между собой линейной зависимостью
Υ = а + bХ,
то коэффициент корреляции Rxy = ±.1.
3.2.58. По одной и той же стартовой позиции противника производится три независимых пуска ракет, причем вероятность попадания в цель одной ракетой равна р. Пусть случайная величина X – число попаданий в цель, а случайная величина Υ – число промахов.
Определить математические ожидания, дисперсии случайных величин X и Υ, а также корреляционный момент и коэффициент корреляции между ними.
Ответ:
3.2.59. Изготавливаемые в цехе втулки сортируются по отклонению их внутреннего диаметра от номинального размера на четыре группы со значениями 0,01, 0,02, 0,03 и 0,04 мм и по овальности на четыре группы со значениями 0,002, 0,004, 0,006 и 0,008 мм. Совместное распределение отклонений диаметра (X) и овальности (Υ) втулок задано таблицей
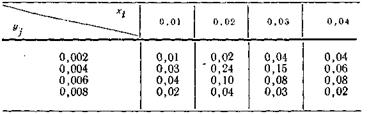
Найти: а) одномерные законы распределения каждой из величин X и Y; б) математические ожидания, средние квадратичные отклонения X и Υ и коэффициент корреляции между ними.
Ответ а) величины X и Υ имеют следующие распределения:
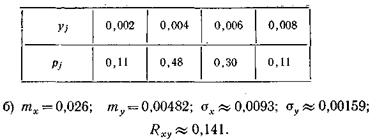
3.2.60. Ряд распределения случайной величины X имеет вид
Вычислить коэффициент корреляции Rxy, если Υ= X2.
Ответ: Rxy = 0.
3.2.61. Случайная величина X имеет математическое ожидание тх и дисперсию σ2; величина Υ связана с X соотношением Υ = ЗХ-2; величина Ζ, в свою очередь, связана с X соотношением Ζ = 3 – 4Х.
Определить: а) корреляционный момент величин Υ и Ζ; б) коэффициент корреляции Υ и Ζ.
Ответ: a) Kyz= -12σx2; б) Rяу= -1.
3.2.62. Система случайных величин (Χ, Υ) имеет следующие характеристики mx = 0, ту = 2, σx2 = 2, σy2 = 1 и коэффициент корреляции Rxy=-1/Ö2.
Найти математическое ожидание и дисперсию случайной величины Ζ = 2Х – ЗУ.
Ответ: mz = -6; σz2 = 29.
3.2.63. Написать выражение для нормальной плотности вероятности W2(x, у) системы двух случайных величин (X, У), если
Ответ:
3.2.64. В радиолокационной системе с разнесенным приемом (рис. 3.3) приемники находятся на таких расстояниях друг от друга, что сигналы Χ, Υ и Ζ статистически независимы. Законы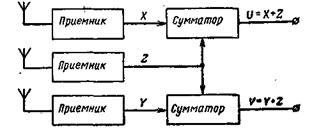 
Рис. 3.3. Схема разнесенного приема с тремя приемниками.
распределения вероятностей для сигналов Χ, Υ и Ζ нормальные с нулевыми средними значениями и дисперсиями σx2 == σy2 == 3, σz2 =12. Найти коэффициент корреляции для напряжений U и V.
Ответ: Ruv = 0,8.
3.2.65. Доказать, что среднее значение квадрата отклонения случайной величины X от ее математического ожидания тх меньше, чем среднее значение квадрата ее отклонения от любого другого числа с, т. е.
3.2.66. Орудие стреляет по цели, для уничтожения которой достаточно двух попаданий.
Зная, что при одном выстреле орудие попадает в цель с вероятностью р, найти математическое ожидание числа произведенных выстрелов, если известно, что стрельба прекращается сразу после уничтожения цели.
Ответ: тх =2/p.
3.2.67. Какому условию должны удовлетворять независимые случайные величины X и Y, чтобы D(XY) = D(X)D(Y).
Ответ: тх =ту=0.
3.2.68. Производится n независимых измерений некоторой физической величины. Результат каждого измерения можно рассматривать как случайную величину Χί с математическим ожиданием т и дисперсией σ2.
Определить: а) математическое ожидание тп и дисперсию σn2 среднего арифметического n измерений; б) относительную ошибку Δ= σn/тп - в определении среднего арифметического.
3.2.69. Найти математическое ожидание тху и дисперсию σxy2 произведения двух независимых случайных величин X и Y, равномерно распределенных соответственно в промежутках (a, b) и (с, d).
Ответ:
3.2.70. Для определения площади квадрата измеряют две его стороны с помощью одного и того же инструмента и результаты измерения перемножают.
С какой относительной средней квадратичной ошибкой Δ = σ/т нужно измерять стороны квадрата для того, чтобы средняя квадратичная ошибка площади была не более 1 %?
Ответ: Δ = 0,71%.
3.2.71. Угол упреждения Υ при воздушной стрельбе определяется формулой
где U – скорость цели; ν – скорость полета снаряда; X – курсовой угол цели.
Найти математическое ожидание ту и среднее квадратичное отклонение σy угла упреждения, если X – случайная величина, равномерно распределенная в интервале от 0 до p/2; U – случайная величина, равномерно распределенная в интервале 600–700 км/час, а ν = 1 км/сек и постоянна (U и X независимы).
Ответ ту = 0,115 рад; σ у = 0,056 рад.
3.2.72. Индикатор кругового обзора радиолокационной станции представляет собой круг радиусом а. Вследствие помех может появиться пятно с центром в любой точке этого круга.
Определить математическое ожидание и дисперсию расстояния R центра пятна от центра круга.
Ответ:
