БИЛИНЕЙНЫЕ КВАДРАТИЧНЫЕ ФОРМЫ
4.1. Линейная функция
Рассмотрим простейшие числовые функции, аргументами которых являются вектора. Простейшей числовой функцией в пространстве L является линейная функция.
ОПРЕДЕЛЕНИЕ 1. Функция 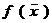 называется линейной, если
называется линейной, если 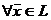 ставит в соответствие число и при этом выполнены условия:
ставит в соответствие число и при этом выполнены условия:
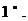
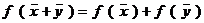 .
.

 .
.
Выберем в n -мерном линейном пространстве  базис
базис 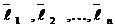 . Так как каждый вектор
. Так как каждый вектор  можно представить в виде:
можно представить в виде:
 ,
,
то в силу свойства  линейной функции имеем:
линейной функции имеем:
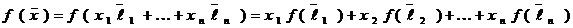 .
.
Итак, в линейном n -мерном пространстве  с заданным базисом линейная функция может быть представлена в виде
с заданным базисом линейная функция может быть представлена в виде
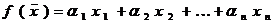 , (1)
, (1)
где  постоянные, зависящие лишь от выбора базиса, а
постоянные, зависящие лишь от выбора базиса, а 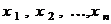 - координаты вектора
- координаты вектора  в этом базисе.
в этом базисе.
Выясним, как меняются коэффициенты линейной функции при замене одного базиса другим.
Пусть 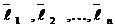 и
и  - два базиса в
- два базиса в  . Предположим, что векторы
. Предположим, что векторы  выражаются через векторы базиса
выражаются через векторы базиса 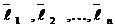 следующим образом:
следующим образом:
 ,
,
В базисе 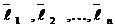 линейная функция
линейная функция 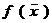 определяется выражением
определяется выражением
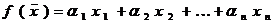 , (2)
, (2)
а в базисе  - выражением
- выражением
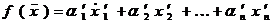 . (3)
. (3)
Так как

то
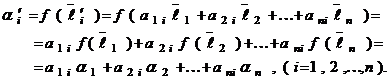
Следовательно, коэффициенты линейной формы преобразуются при переходе к другому базису так же, как векторы базиса этого пространства.
4.2. Билинейные формы
ОПРЕДЕЛЕНИЕ 2. Выражение  называется билинейной функцией (билинейной формой) от векторов
называется билинейной функцией (билинейной формой) от векторов  и
и  , если:
, если:
 . При фиксированном
. При фиксированном 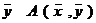 есть линейная функция от
есть линейная функция от  , то есть:
, то есть:
а)  ,
,
б) 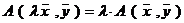 .
.
 . При фиксированном
. При фиксированном 
 есть линейная функция от
есть линейная функция от  , то есть:
, то есть:
а) 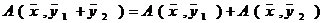 ,
,
б)  .
.
ОПРЕДЕЛЕНИЕ 3. Билинейная функция (форма) называется симметричной, если для всех векторов  и
и  имеет место равенство:
имеет место равенство:
 (4)
(4)
В частности, из определения скалярного произведения  в евклидовом пространстве Е следует, что это произведение является симметричной билинейной формой.
в евклидовом пространстве Е следует, что это произведение является симметричной билинейной формой.
4.3. Матрицы билинейной формы
Выберем в n -мерном пространстве  какой-либо базис
какой-либо базис 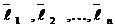 и выразим билинейную форму
и выразим билинейную форму  через коэффициенты
через коэффициенты  и
и 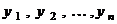 векторов
векторов  и
и  в этом базисе. Имеем:
в этом базисе. Имеем:

В силу свойств а) и б) пункта  билинейной формы, имеем:
билинейной формы, имеем:

Или, короче:
 .
.
Обозначим постоянные 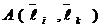 через
через 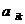 . Тогда в заданном базисе
. Тогда в заданном базисе 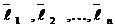 всякая билинейная форма в n -мерном пространстве может быть записана в виде:
всякая билинейная форма в n -мерном пространстве может быть записана в виде:
 . (5)
. (5)
ОПРЕДЕЛЕНИЕ 4. Матрицу 
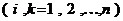 , составленную из коэффициентов
, составленную из коэффициентов 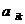 многочлена (5), называют матрицей билинейной формы
многочлена (5), называют матрицей билинейной формы  в базисе
в базисе 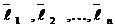
Таким образом, в каждом базисе пространства  билинейная форма
билинейная форма  определяется своей матрицей:
определяется своей матрицей:
 .
.
4.4. Преобразование матрицы билинейной формы
При изменении базиса
Пусть даны в n -мерном линейном пространстве  два базиса:
два базиса: 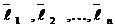 и
и  . Причем, векторы второго базиса
. Причем, векторы второго базиса  выражаются через векторы базиса
выражаются через векторы базиса 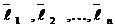 формулами:
формулами:

Матрицу
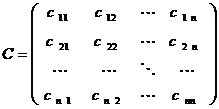
назовем матрицей перехода от базиса 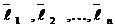 к базису
к базису  .
.
Пусть 
 есть матрица билинейной формы
есть матрица билинейной формы  в базисе
в базисе 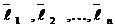 , а
, а  матрица той же билинейной формы в базисе
матрица той же билинейной формы в базисе  . Наша задача состоит в том, чтобы по матрице
. Наша задача состоит в том, чтобы по матрице 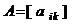
 найти матрицу
найти матрицу 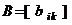
 .
.
По определению  , то есть
, то есть 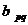 - значение билинейной формы
- значение билинейной формы  при
при 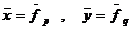 .
.
Для того, чтобы найти это значение, то есть 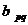 , воспользуемся формулой (5), подставив в нее вместо
, воспользуемся формулой (5), подставив в нее вместо  и
и  координаты векторов
координаты векторов  и
и  в базисе
в базисе 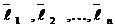 , то есть числа
, то есть числа  и
и  . Получим:
. Получим:
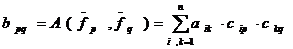 . (6)
. (6)
Это и есть искомая формула.
Запишем ее в матричной форме. Для этого положим  . Таким образом,
. Таким образом,  является элементами матрицы
является элементами матрицы 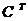 , транспонированной к матрице С. С учетом этого выражение (6) можно записать так:
, транспонированной к матрице С. С учетом этого выражение (6) можно записать так:

или
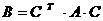 .
.
Итак, если А и В суть матрицы билинейной формы  соответственно в базисах
соответственно в базисах 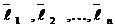 и
и  ., то преобразование матрицы билинейной формы при переходе от одного базиса к другому будет иметь вид:
., то преобразование матрицы билинейной формы при переходе от одного базиса к другому будет иметь вид:
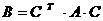
где С - матрица перехода от базиса 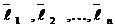 к базису
к базису  ., а
., а 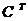 - транспонированная матрица.
- транспонированная матрица.
4.5. Квадратичные формы
Пусть -  симметричная билинейная форма.
симметричная билинейная форма.
ОПРЕДЕЛЕНИЕ 1. Функция 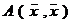 , которая получается из билинейной формы
, которая получается из билинейной формы  , если положить в ней
, если положить в ней  =
=  , называется квадратичнойформой.
, называется квадратичнойформой.
Всякая квадратичная форма 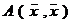 , в базисе
, в базисе 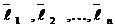 евклидового пространства Еn выражается следующей формулой:
евклидового пространства Еn выражается следующей формулой:
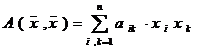 , (7)
, (7)
где 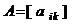
 симметричная матрица
симметричная матрица 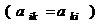 квадратичной формы и
квадратичной формы и  .
.
В некотором базисе выражение (7) квадратичной формы может не содержать произведений  , то есть
, то есть
 , (8)
, (8)
Выражение (8) называется каноническим видом квадратичной формы. В частности, если  , то получаем нормальный видквадратичной формы
, то получаем нормальный видквадратичной формы 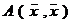 .
.
Для всякой квадратичной формы существует такой базис, в котором она имеет канонический вид.
4.6. Методы приведения квадратичной формы
К каноническому виду
а) Метод Лагранжа выделения полных квадратов.
Пусть квадратичная форма  имеет в базисе
имеет в базисе 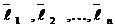 вид (7). Для приведения формы
вид (7). Для приведения формы 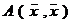 к сумме квадратов методом Лагранжа рассмотрим случай квадратичной формы, у которой все коэффициенты
к сумме квадратов методом Лагранжа рассмотрим случай квадратичной формы, у которой все коэффициенты  (при квадратах
(при квадратах 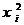 ),
),  равны нулю и в то же время эта квадратичная форма не равна тождественно нулю, то есть в ней есть отличное от нуля хотя бы одной произведение, например,
равны нулю и в то же время эта квадратичная форма не равна тождественно нулю, то есть в ней есть отличное от нуля хотя бы одной произведение, например, 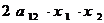 .
.
Выполним преобразование базиса, при котором коэффициенты векторов в старом и новом базисах связаны формулами:
 .
.
Тогда:
 .
.
Таким образом, всегда найдется такой базис, в котором в записи (7) хотя бы один коэффициент при квадрате 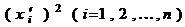 .отличен от нуля.
.отличен от нуля.
В дальнейшем будем считать, что  . (Если
. (Если  , то отличен от нуля коэффициент при квадрате какой-нибудь другой координаты и к рассматриваемому случаю можно прийти, иначе, занумеровав векторы
, то отличен от нуля коэффициент при квадрате какой-нибудь другой координаты и к рассматриваемому случаю можно прийти, иначе, занумеровав векторы  , что также является некоторым преобразованием базиса).
, что также является некоторым преобразованием базиса).
Рассмотрим часть квадратичной формы, содержащей  , то есть
, то есть
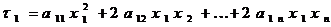 .
.
Дополним эту сумму до полного квадрата:
 ,
,
где 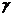 есть алгебраическая сумма членов, не зависящих от
есть алгебраическая сумма членов, не зависящих от  . Если теперь сделать замену
. Если теперь сделать замену

то квадратичная форма в новом базисе примет вид
 .
.
В полученной форме выделено слагаемое  , а оставшаяся часть А, является квадратичной формой в
, а оставшаяся часть А, является квадратичной формой в  .
.
Далее эти рассуждения повторяются для исходной квадратичной формы 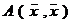 и т.д. Конечным результатом является то, что она приводится к нормальной форме.
и т.д. Конечным результатом является то, что она приводится к нормальной форме.
ПРИМЕР 1. Методом Лагранжа привести к каноническому виду квадратичную форму
 .
.
Первое преобразование:
 .
.
Тогда получим:
 .
.
Второе преобразование:
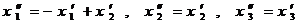 .
.
Получим новое выражение для квадратичной формы:
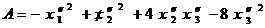 .
.
Третье преобразование:
 .
.
форма примет канонический вид:
 .
.
При этом
 .
.
б) Метод собственных векторов.
Будем рассматривать квадратичную форму (7) в евклидовом пространстве
 . Так как матрица
. Так как матрица 
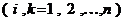 симметрична, то она может быть представлена
симметрична, то она может быть представлена
в виде:
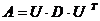
где – D диагональная матрица, на диагонали которой стоят собственные числа матрицы А, а U - ортогональная матрица, столбцами которой являются собственные вектора матрицы А. Как ранее отмечалось, что эти вектора в случае различных собственных чисел матрицы А являются линейно независимыми и образуют базис в  .
.
Столбцы матрицы U являются координатами некоторого ортонормированного базиса 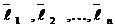 , в котором матрицa А имеет диагональный вид, и, следовательно, квадратичная форма – искомый канонический вид.
, в котором матрицa А имеет диагональный вид, и, следовательно, квадратичная форма – искомый канонический вид.
Соответствующее преобразование координат определяется соотношением:
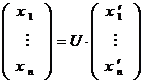 .
.
ПРИМЕР 2. Найти ортогональное преобразование, приводящее квадратичную форму
 ,
,
заданную в евклидовом пространстве  , к каноническому виду. Написать этот канонический вид.
, к каноническому виду. Написать этот канонический вид.
Матрица квадратичной формы имеет вид:
 .
.
Определим собственные числа этой матрицы. Имеем:
 .
.
Раскрывая определитель, находим корни характеристического многочлена, которые являются собственными числами матрицы А. Итак, собственные числа этой матрицы суть 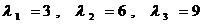 .
.
Соответствующие ортонормированные собственные векторы:

и, следовательно,
 .
.
В базисе  заданная квадратичная форма имеет вид:
заданная квадратичная форма имеет вид:
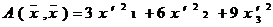 ,
,
а соответствующее преобразование координат:
 .
.