Запишем формулу для молярной теплоемкости в предположении о равнораспределении энергии по степеням свободы.
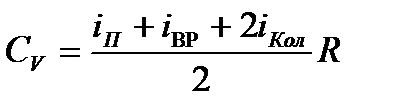. (1)
где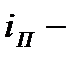 
число поступательных, 
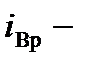вращательных, 
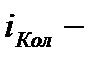колебательных степеней свободы. Коэффициент при 
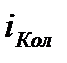отражает тот факт, что в колебательном движении имеется равные средняя кинетическая и средняя потенциальная энергии.
а) Для двухатомных молекул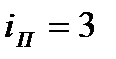 
- число координат центра масс, 
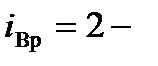две угловые координаты, задающие ориентацию молекулярной оси. 
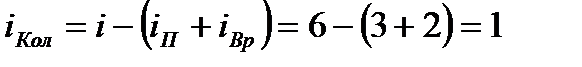, где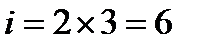 
- полное число степеней свободы системы, состоящей из двух молекул.
Тогда
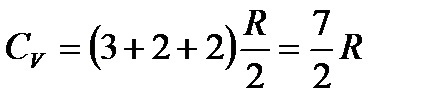. (2)
б) Линейные N -атомные молекулы.
Полное число степеней свободы 
; из этих степеней свободы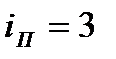 
(число координат центра масс), 
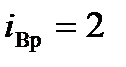(ориентация молекулярной оси). Отсюда 
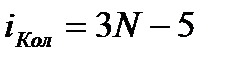. Теплоемкость равна
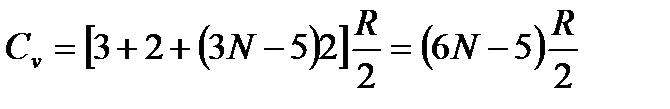. (3)
в) Объемные молекулы.
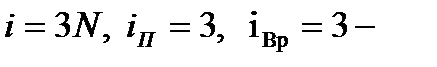поскольку для нелинейных молекул появляется необходимость задания угла поворота относительно оси молекулы. Заметим, что любое твердое тело имеет три вращательных степени свободы. Окончательно имеем
.
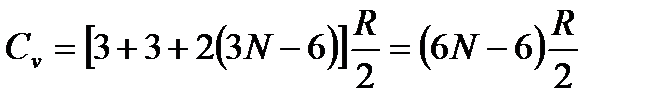Адиабатический процесс. Уравнение Пуассона.
Процесс, происходящий в системе без теплообмена с окружающей средой, называется адиабатическим.
Установим связь между параметрами идеального газа, совершающего квазистатический адиабатический процесс. Положив в уравнении (38)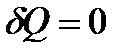 
и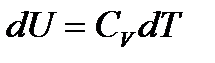 
, приводим I начало к виду:
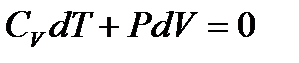. (1.25)
Дифференцируя уравнение Менделеева-Клапейрона, получим
.
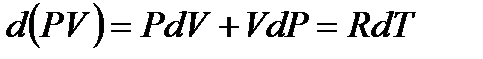Отсюда, используя уравнение Роберта Майера, имеем
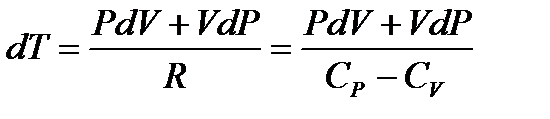. (1.26)
Выражая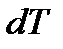 
из (1.25), находим
.
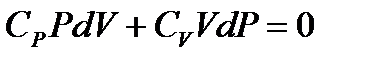Используя введенное обозначение
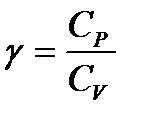, (1.27)
приводим последнее уравнение к виду:
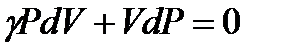. (1.28)
Мы получили дифференциальное уравнение, описывающее квазистатический адиабатический процесс, проводимый с идеальным газом.
Теплоемкост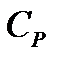и 
и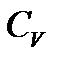 
идеального газа, вообще говоря, зависят от температуры, однако во многих случаях они остаются практически постоянными в широком интервале температур. Понятно, что постоянным будет и их отношение 
.
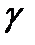При этом условии уравнение (1.28) легко интегрируется
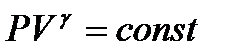. (1.29)
Полученное соотношение называется уравнением Пуассона (1781 – 1840). Оно является уравнением адиабаты – кривой, изображающей квазистатический адиабатический процесс.
Величина 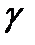называется показателем адиабаты, или адиабатической постоянной.
Поскольку переменные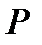 
, 
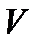и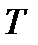 
для идеального газа связаны уравнением 
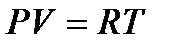, то уравнение адиабаты можно записать как
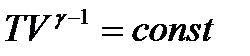, (1.30)
или
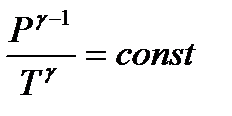. (1.31)
Так как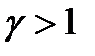 
, то из уравнения (1.30) следует, что при адиабатическом сжатии газ будет нагреваться (механизм воспламенения горючей смеси в дизелях), а при адиабатическом расширении – охлаждаться. Нагревание газа при адиабатическом сжатии объясняется тем, что производимая внешними силами работа идет на увеличение внутренней энергии газа. Если газ идеальный, то, как следует из (1.21), увеличение его внутренней энергии будет проявляться в повышении его температуры. Аналогично объясняется охлаждение газа при адиабатическом расширении.
Политропические процессы.
Процессы, идущие при постоянной теплоемкости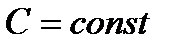 
, называются политропическими процессами. Найдем уравнение политропического процесса. Из первого начала имеем для одного моля:
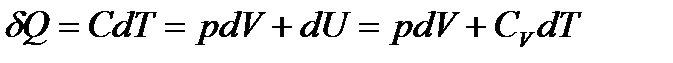. (3.9)
Откуда, учитывая
,
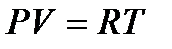получаем
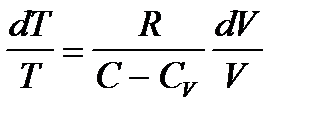(3.10)
Решая дифференциальное уравнение (3.10), находим уравнение политропического процесса в переменных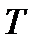 
и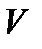 
:
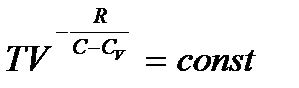. (3.11)
Обозначим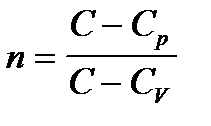 
и учтем, что 
.
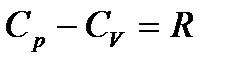Тогда уравнение политропического процесса принимает вид:
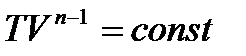(3.12)
где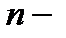 
показатель политропы.
Используя снова уравнение состояния, получаем
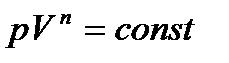(3.13)
В частности, все элементарные процессы (изобарический, изохорический и изотермический) являются политропическими и их уравнения получаются из (3.12 и 3.13).