То есть, если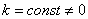 
, то 
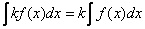
Доказательство: а вы как думали? =)
Найдём производную левой части. Используем свойство № 1:
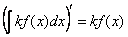
Найдём производную правой части. Используем правило дифференцирования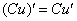 
и свойство № 1:
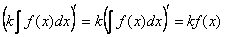
Получены одинаковые результаты, из чего и следует справедливость данного свойства.
Вообще, многие доказательства не столько сложны, сколько занудны и формальны – используются определения, ранее доказанные свойства, теоремы и т.д. Но, несмотря на их сухость, немалая часть студентов входит во вкус и даже начинает читать учебники по высшей математике в любой свободный момент =) Будьте осторожны =)
4) Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:
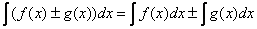
Справедливо для любого количества слагаемых.
Свойство проверяется точно так же, как и предыдущее – берутся производные от обеих частей. Но доказывать его я, пожалуй, не буду – хорошего понемножку =)
Решить неопределенный интеграл 
– это значит ПРЕВРАТИТЬ его в определенную функцию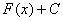 
, пользуясь некоторыми правилами, приемами и таблицей.
Возьмем, например, табличный интеграл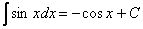 
. Что произошло? 
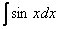превратился в функцию 
.
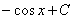Как и в случае с производными, для того, чтобы научиться находить интегралы, не обязательно быть в курсе, что такое интеграл, первообразная функция с теоретической точки зрения. Достаточно просто осуществлять превращения по некоторым формальным правилам. Так, в случае 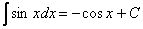совсем не обязательно понимать, почему интеграл 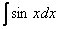превращается именно в 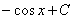. Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны.
Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найдена правильно, справедливо следующее:
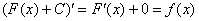
Иными словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.
Вернемся к тому же табличному интегралу .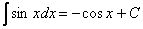
Убедимся в справедливости данной формулы. Берем производную от правой части:
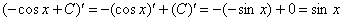– исходная подынтегральная функция.
Вот, кстати, стало понятнее, почему к функции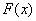 
всегда приписывается константа 
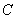. При дифференцировании константа всегда превращается в ноль.
Решить неопределенный интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию. В рассматриваемом табличном примере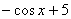 
, 
, 
, 
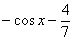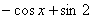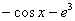и т. д. – все эти функции являются решением интеграла 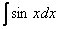. Решений бесконечно много, поэтому записывают коротко: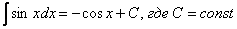 
Таким образом, любой неопределенный интеграл достаточно легко проверить (в отличие от производных, где хорошую стопудовую проверку можно осуществить разве что с помощью математических программ). Это некоторая компенсация за большое количество интегралов разных видов.
Переходим к рассмотрению конкретных примеров. Начнем, как и при изучении производной,
с двух правил интегрирования, которые также называют свойствами линейности неопределенного интеграла:
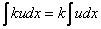– постоянный множитель можно (и нужно) вынести за знак интеграла.
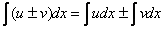– интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.
Как видите, правила, в принципе, такие же, как и для производных.
Пример 1
Найти неопределенный интеграл. Выполнить проверку.
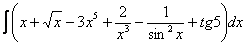
Решение: Удобнее переписать его на бумагу.
(1) Применяем правило 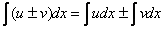. Не забываем записать значок дифференциала 
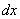под каждым интегралом. Почему под каждым? 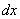– это полноценный множитель, если расписывать решение совсем детально, то первый шаг следует записать так:
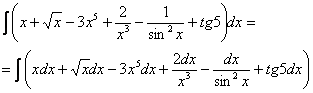
(2) Согласно правилу 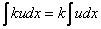, выносим все константы за знаки интегралов. Обратите внимание, что в последнем слагаемом 
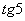– это константа, её также выносим.
Кроме того, на данном шаге готовим корни и степени для интегрирования. Точно так же, как и при дифференцировании, корни надо представить в виде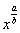 
. Корни и степени, которые располагаются в знаменателе – перенести вверх.
! Примечание: в отличие от производных, корни в интегралах далеко не всегда следует приводить к виду 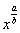, а степени переносить вверх. Например, 
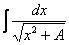– это готовый табличный интеграл, и всякие китайские хитрости вроде 
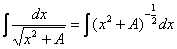совершенно не нужны. Аналогично: 
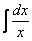– тоже табличный интеграл, нет никакого смысла представлять дробь в виде 
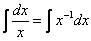. Внимательно изучите таблицу!
(3) Все интегралы у нас табличные. Осуществляем превращение с помощью таблицы, используя формулы: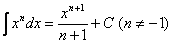 
, 
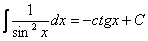и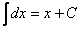 
.
Особое внимание обращаю на формулу интегрирования степенной функции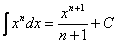 
, она встречается очень часто, ее лучше запомнить. Следует отметить, что табличный интеграл 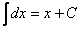– частный случай этой же формулы: 
.
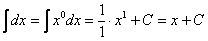Константу 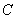достаточно приплюсовать один раз в конце выражения (а не ставить их после каждого интеграла).
(4) Записываем полученный результат в более компактном виде, все степени вида 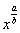снова представляем в виде корней, степени с отрицательным показателем – сбрасываем обратно в знаменатель.
Проверка. Для того чтобы выполнить проверку нужно продифференцировать полученный ответ:
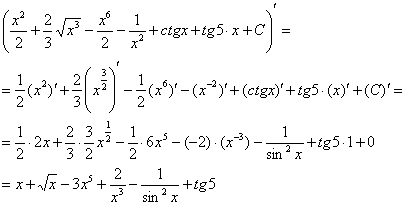
Получена исходная подынтегральная функция, значит, интеграл найден правильно. От чего плясали, к тому и вернулись. Знаете, очень хорошо, когда история с интегралом заканчивается именно так.