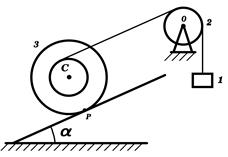
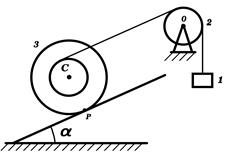
 Задача 1.1. Каток 3 начинает подниматься без скольжения вверх по наклонной плоскости с помощью троса, намотанного на малый барабан катка, блока 2 с неподвижной осью и тяжелого груза 1 на конце троса. Найти движение тел 1 – 3, если известна масса
Задача 1.1. Каток 3 начинает подниматься без скольжения вверх по наклонной плоскости с помощью троса, намотанного на малый барабан катка, блока 2 с неподвижной осью и тяжелого груза 1 на конце троса. Найти движение тел 1 – 3, если известна масса  катка, массы
катка, массы 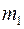 и
и 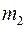 груза и блока, радиусы R и r большого и малого цилиндров катка, а также момент инерции катка I относительно оси, проходящей через центр масс С катка перпендикулярно к основанию цилиндров. Угол наклона плоскости с горизонтом равен
груза и блока, радиусы R и r большого и малого цилиндров катка, а также момент инерции катка I относительно оси, проходящей через центр масс С катка перпендикулярно к основанию цилиндров. Угол наклона плоскости с горизонтом равен  .
.
Решение. Включим в систему три движущихся тела. Они взаимодействуют между собой, а также с Землей и наклонной поверхностью. Система имеет одну степень свободы.
Связи системы идеальны: нить невесома, нерастяжима и не проскальзывает по телу 2, реакция наклонной плоскости не работает при качении тела 1 без проскальзывания.
Виртуальные перемещения тел, а также кинематические характеристики движения связаны следующими уравнениями:
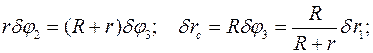
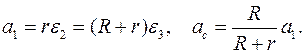
Принимаем за независимое виртуальное перемещение системы перемещение 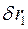 для груза 1 вниз по вертикали.
для груза 1 вниз по вертикали.
Главные векторы сил инерции 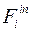 и главные моменты сил инерции вращающихся тел
и главные моменты сил инерции вращающихся тел 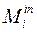 , с учетом уравнений связей, имеют вид:
, с учетом уравнений связей, имеют вид:
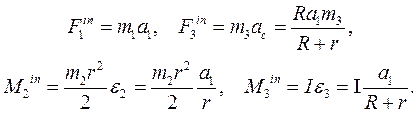
Дифференциальный принцип механики запишем в следующем виде:
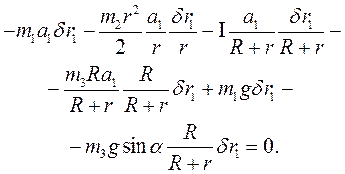
Сокращая это уравнение на 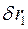 , получим дифференциальное уравнение движения системы. Его решение показывает, что равноускоренное движение груза 1 происходит с ускорением
, получим дифференциальное уравнение движения системы. Его решение показывает, что равноускоренное движение груза 1 происходит с ускорением
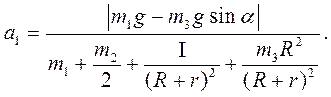
В силу уравнений связей другие тела вращаются равноускоренно.
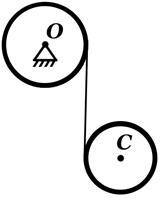
Задача 2.1. Два однородных сплошных диска c массами 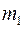 ,
, 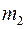 и радиусами r1, r2 соединены невесомой лентой, намотанной на диски. Первый диск вращается вокруг неподвижной горизонтальной оси О, когда второй, разматывая ленту с обоих дисков, падает, так, что его центр масс С движется вертикально. Найти ускорение центра масс С падающего диска.
и радиусами r1, r2 соединены невесомой лентой, намотанной на диски. Первый диск вращается вокруг неподвижной горизонтальной оси О, когда второй, разматывая ленту с обоих дисков, падает, так, что его центр масс С движется вертикально. Найти ускорение центра масс С падающего диска.
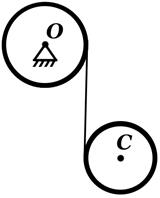 Решение. За два независимых параметра, определяющих движение системы, выберем углы поворота θ1 и θ2 цилиндров.
Решение. За два независимых параметра, определяющих движение системы, выберем углы поворота θ1 и θ2 цилиндров.
Рассматривая движение второго цилиндра как сложное – переносное вместе с лентой и относительное по отношению к ленте, по теоремам о сложении скоростей и ускорений точки С получим уравнения связей в кинематическом виде для движения:
Уравнения связей в вариациях:
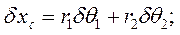
Кинематическая форма уравнений связей:
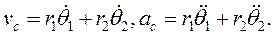
Связи системы идеальны, поэтому принцип Даламбера - Лагранжа позволяет приравнять к нулю элементарную работу всех активных сил, всех сил инерций и всех моментов сил инерций системы на каждом из независимых виртуальных перемещений δθ1 и δθ2: 
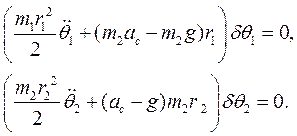
В результате получим:
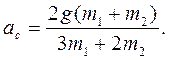
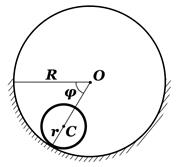 Задача 3.1.Однородный сплошной цилиндр массой
Задача 3.1.Однородный сплошной цилиндр массой 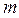 и радиусом основания r скатывается вниз без скольжения по неподвижной цилиндрической поверхности с радиусом основания R из начального состояния покоя, определяемого углом
и радиусом основания r скатывается вниз без скольжения по неподвижной цилиндрической поверхности с радиусом основания R из начального состояния покоя, определяемого углом 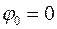 . Написать дифференциальное уравнение движения цилиндра.
. Написать дифференциальное уравнение движения цилиндра.
Решение. Для решения задачи применим дифференциальный принцип механики, позволяющий найти как движение цилиндра, так его взаимодействие с цилиндрической поверхностью.
Цилиндр имеет одну степень свободы. Необходимые характеристики его действительного движения имеют вид:
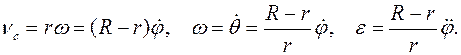 Здесь
Здесь 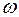 и
и  есть угловая скорость и угловое ускорение цилиндра.
есть угловая скорость и угловое ускорение цилиндра.
Для возможных перемещений уравнения связей запишутся в виде:
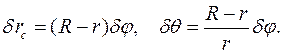
Главный вектор сил инерций 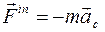 и главный момент сил инерций
и главный момент сил инерций 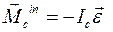 цилиндра имеют вид соответственно:
цилиндра имеют вид соответственно:
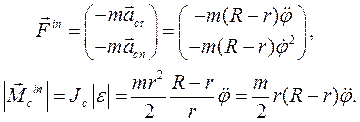
Элементарная работа силы тяжести равна
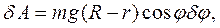
а сумма элементарных работ главного вектора и главного момента сил инерций на возможном (виртуальном) перемещении равна
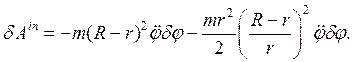
Принцип Даламбера – Лагранжа примет вид:
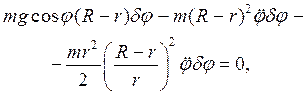
откуда следует: 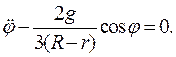
Это есть дифференциальное уравнение движения цилиндра.
Подчеркнем, что возможные (виртуальные) перемещения совместимы со связями, то есть удовлетворяют уравнениям связей, и выражены по уравнениям связей через независимое (возможное) перемещение 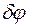 .
.
Дифференциальный принцип механики на перемещениях, не совместимых со связями.
На элементарных перемещениях системы 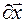 , не совместимых со связями, дифференциальный принцип механики применяется тогда, когда движение системы известно (найдено), а необходимо найти силы контактного взаимодействия (силы реакций связей).
, не совместимых со связями, дифференциальный принцип механики применяется тогда, когда движение системы известно (найдено), а необходимо найти силы контактного взаимодействия (силы реакций связей).
Для каждого тела системы с номером s, s = 1, 2, …, N, элементарные перемещения 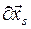 могут быть двух типов. Это либо поступательное перемещение (трансляция)
могут быть двух типов. Это либо поступательное перемещение (трансляция) 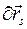 , либо элементарный поворот
, либо элементарный поворот 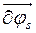 . Поэтому для N тел дифференциальный принцип можно записать так:
. Поэтому для N тел дифференциальный принцип можно записать так:

Здесь для каждого тела 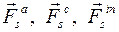 есть главные векторы активных сил, сил контактного взаимодействия и сил инерций соответственно, а
есть главные векторы активных сил, сил контактного взаимодействия и сил инерций соответственно, а 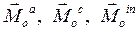 есть главные моменты соответствующих сил относительно полюса трансляции О.
есть главные моменты соответствующих сил относительно полюса трансляции О.
Принцип применим к любому количеству тел (одному телу) системы.
Так как 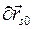 ,
, 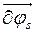 не удовлетворяют уравнениям связей, то они произвольны и независимы. Тогда, взяв за полюс центр масс тела С, имеем:
не удовлетворяют уравнениям связей, то они произвольны и независимы. Тогда, взяв за полюс центр масс тела С, имеем:
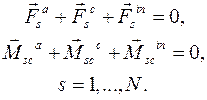
Для одного твердого тела (N = 1) из определений главного вектора сил инерций 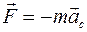 и главного момента сил инерций
и главного момента сил инерций  , следуют дифференциальные уравнения движения абсолютно твердого тела, причем второе уравнение записано в подвижном базисе:
, следуют дифференциальные уравнения движения абсолютно твердого тела, причем второе уравнение записано в подвижном базисе:
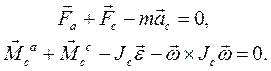
Это есть теорема о движении центра масс тела в неподвижном базисе и теорема об изменении момента импульса относительно центра масс, записанная в подвижном базисе.
 Задача 1.2.
Задача 1.2.
Дифференциальное уравнение системы уже было написано в задаче 1.1. Чтобы написать уравнения, движения, включающие силы реакций взаимодействия тел 1-3 между собой и с другими телами системы всех взаимодействующих тел материальной системы, достаточно к каждому движущемуся телу применить дифференциальный принцип механики на элементарных перемещениях, не совместимых со связями. Силы 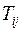 ,
, 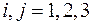 реакций троса c двух различных сторон от блока, сила трения
реакций троса c двух различных сторон от блока, сила трения 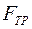 и нормальная реакция N катка входят в следующие уравнения:
и нормальная реакция N катка входят в следующие уравнения:
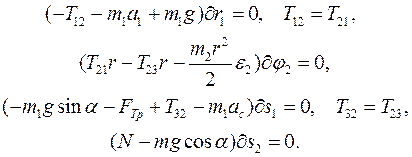
Элементарные поступательные перемещения 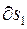 и
и 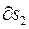 , вдоль наклонной плоскости и перпендикулярно к ней, не совместимы со связями.
, вдоль наклонной плоскости и перпендикулярно к ней, не совместимы со связями.
Четыре уравнения имеют четыре неизвестных силы реакции (движение тел системы уже было найдено).
Задача 2.2. В задаче 2.1 движение было найдено выше. Найти силу реакции 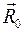 оси О и силу реакции
оси О и силу реакции  ленты.
ленты.
 Решение. Применим дифференциальный принципк двум цилиндрам на их поступательном перемещении
Решение. Применим дифференциальный принципк двум цилиндрам на их поступательном перемещении  вверх по вертикали, не совместимом со связями, а затем ко второму цилиндру на его поступательном перемещении вниз по вертикали
вверх по вертикали, не совместимом со связями, а затем ко второму цилиндру на его поступательном перемещении вниз по вертикали  , не совместимом со связями. В результате получим два уравнения с двумя неизвестными (ускорение
, не совместимом со связями. В результате получим два уравнения с двумя неизвестными (ускорение 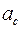 уже найдено в задаче):
уже найдено в задаче):
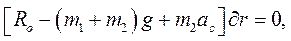
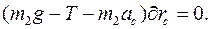
Ответ:
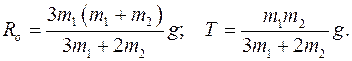
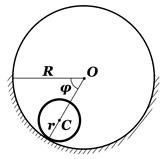 Задача 3.2. В условиях задачи 3.1, найти компоненты силы реакции цилиндрической поверхности как функции угла
Задача 3.2. В условиях задачи 3.1, найти компоненты силы реакции цилиндрической поверхности как функции угла 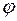 , определяющего движение центра масс С цилиндра.
, определяющего движение центра масс С цилиндра.
Силу реакции в точке касания цилиндра с поверхностью разложим на нормальную реакцию 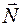 и силу трения
и силу трения 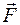 . Для вычисления компонент силы реакции связи применим дифференциальный принцип механики на элементарных перемещениях, не совместимых со связями. Каждое из них независимо, поэтому на каждом из них сумма элементарных работ активных сил и сил инерций равна нулю. За элементарные перемещения возьмем поступательные элементарные перемещения
. Для вычисления компонент силы реакции связи применим дифференциальный принцип механики на элементарных перемещениях, не совместимых со связями. Каждое из них независимо, поэтому на каждом из них сумма элементарных работ активных сил и сил инерций равна нулю. За элементарные перемещения возьмем поступательные элементарные перемещения 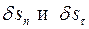 в направлении нормали и в направлении касательной к неподвижной цилиндрической поверхности в точке касания цилиндра с поверхностью. Соответствующие уравнения имеют вид:
в направлении нормали и в направлении касательной к неподвижной цилиндрической поверхности в точке касания цилиндра с поверхностью. Соответствующие уравнения имеют вид:
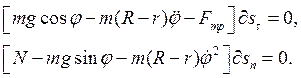
Эти уравнения после сокращения на элементарные перемещения совпадают по форме с теоремой о движении центра масс цилиндра.
Для нахождения нормальной реакции поверхности в зависимости от положения цилиндра необходимо проинтегрировать дифференциальное уравнение движения. Но так как работающая сила тяжести является потенциальной силой, результатом первого интегрирования будет закон сохранения механической энергии
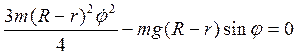 .
.
Результаты вычислений дают следующие выражения для компонентов силы реакции:

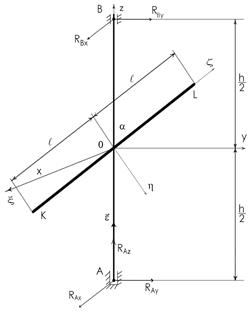 Задача 4. Мещерский, (42.10). Однородный стержень KL, жестко прикрепленный в его центре масс под углом α к оси АВ,вращается равноускоренно вокруг этой оси с угловым ускорением
Задача 4. Мещерский, (42.10). Однородный стержень KL, жестко прикрепленный в его центре масс под углом α к оси АВ,вращается равноускоренно вокруг этой оси с угловым ускорением 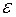 . Определить силы динамического давления оси АВ на подпятник А и подшипник В, если: М – масса стержня,
. Определить силы динамического давления оси АВ на подпятник А и подшипник В, если: М – масса стержня, 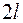 - его длина,
- его длина, 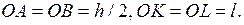 В начальный момент система покоилась.
В начальный момент система покоилась.
Решение. Силы реакций можно разделить на две части: одну часть, которая зависит от сил тяжести, и другую, которая вызвана вращением тела вокруг оси. Следуя условиям задачи, во всех уравнениях ее решения нет сил тяжести и их моментов, а найденные силы реакций связей называют динамические (добавочные) силы реакций. Динамические давления равны им по величине, а их проекции имеют противоположные знаки.
Применим дифференциальный принцип на перемещениях, не совместимых со связями. Так как они независимы, то на любом элементарном перемещении равна нулю сумма работ всех сил динамических реакций и главного момента сил инерций (главный вектор сил инерций равен нулю). Записывая необходимые характеристики главного момента сил инерций в главных центральных осях Оξηζ, связанных со стержнем (смотри рисунок), имеем:
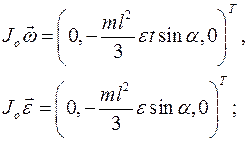
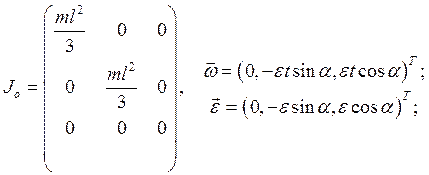
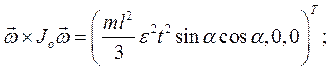
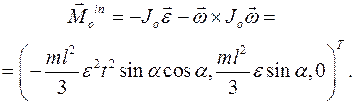
Выберем в качестве элементарных перемещений повороты вокруг осей системы координат Оxyz и поступательные перемещения системы (стержень KL плюс ось АВ) вдоль этих осей.
Поворот 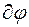 вокруг оси Оx:
вокруг оси Оx:
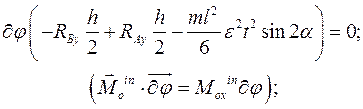
перемещение  вдоль оси
вдоль оси 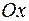 :
:
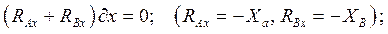
перемещение 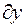 вдоль оси Оy:
вдоль оси Оy:
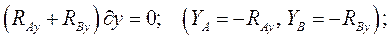
поворот 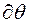 вокруг оси Оy:
вокруг оси Оy:
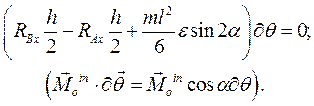
Решая систему уравнений, получим:
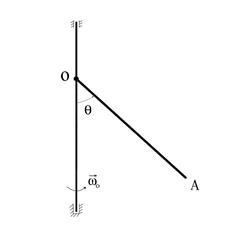
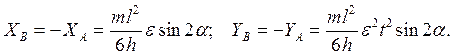
Задача 5. Однородный тонкий стержень 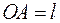 может качаться вокруг горизонтальной оси О в вертикальной плоскости, в то время как плоскость его качания вращается вокруг неподвижной вертикальной оси, проходящей через точку О, с постоянной угловой скоростью
может качаться вокруг горизонтальной оси О в вертикальной плоскости, в то время как плоскость его качания вращается вокруг неподвижной вертикальной оси, проходящей через точку О, с постоянной угловой скоростью  . Найти постоянный острый угол
. Найти постоянный острый угол 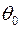 в относительном положении равновесия стержня.
в относительном положении равновесия стержня.
Решение. Их принципа Даламбера - Лагранжа при идеальности связей
имеем: 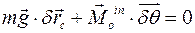 ,
,
где, так как 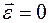 , момент сил инерций имеет вид:
, момент сил инерций имеет вид:
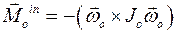 .
.
В подвижных осях 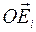 ,
, 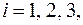 первая из которых направлена вдоль OA, имеем:
первая из которых направлена вдоль OA, имеем:
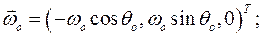
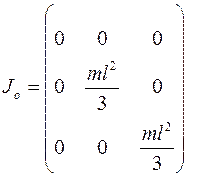
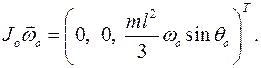
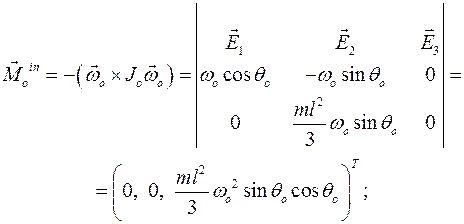 Окончательно уравнение принципа запишется так:
Окончательно уравнение принципа запишется так:
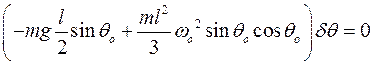 . Откуда, если
. Откуда, если 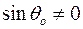 , получаем ответ:
, получаем ответ:
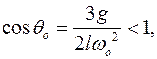 , если
, если 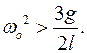
Положения равновесия консервативных систем.
Консервативная система имеет геометрические стационарные связи, а все работающие силы потенциальны.
Положения равновесия определяются свойствами сил взаимодействий и виртуальными перемещениями в этих положениях.
А именно: в каждом положении равновесия равны нулю виртуальные работы силового поля и поля реакций связей на любых виртуальных перемещениях:
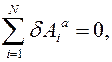
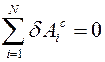 .
.
Это свойство сил взаимодействий примем за определение положений равновесия.
Но так как для потенциальных сил в положениях равновесия виртуальную работу можно выразить через дифференциал потенциальной энергии, то есть
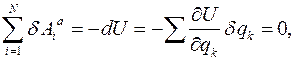
то равенство нулю полного дифференциала  потенциальной энергии
потенциальной энергии 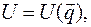
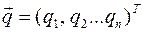 , означает, что положения равновесия доставляют экстремум потенциальной энергии.
, означает, что положения равновесия доставляют экстремум потенциальной энергии.
Следующее определение положений равновесия консервативной системы тождественно предыдущему.
Положениями равновесия консервативной системы с идеальными связями называются такие положения системы 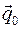 , совместимые со связями, в которых потенциальная энергия системы U принимает экстремальные значения:
, совместимые со связями, в которых потенциальная энергия системы U принимает экстремальные значения:
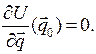
Это определение не связано с движениями системы, и, таким образом, не зависит от начальных состояний системы (начальных положений и начальных скоростей тел).
Так как связи системы идеальны, то из принципа Даламбера – Лагранжа следует, что на движениях системы в положениях равновесия равна нулю и виртуальная работа сил инерций.
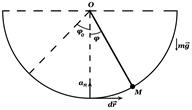 Пример 1. Математический маятник: материальная точка М движется по части окружности
Пример 1. Математический маятник: материальная точка М движется по части окружности 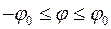
в вертикальной плоскости. В нижней точке равны нулю виртуальные работы силы тяжести и силы реакции нити. Это есть положение равновесия. Заметим, что на границе интервала виртуальная работа силы тяжести (и силы инерции) не равны нулю, поэтому граница интервала не есть положение равновесия, хотя потенциальная энергия математического маятника в ней имеет максимум.
 Пример. Сферический маятник: материальная точка подвешена на нити в точке О, центре сферы. Хотя сила тяжести и сила реакции нити не работают на элементарных перемещениях, векторы которых являются касательными векторами к параллелям сферы, однако они работают на виртуальных перемещениях, касательных к меридианам сферы. В нижней точке полусферы эти силы не работают на всех виртуальных перемещениях, поэтому нижняя точка есть положение равновесия маятника.
Пример. Сферический маятник: материальная точка подвешена на нити в точке О, центре сферы. Хотя сила тяжести и сила реакции нити не работают на элементарных перемещениях, векторы которых являются касательными векторами к параллелям сферы, однако они работают на виртуальных перемещениях, касательных к меридианам сферы. В нижней точке полусферы эти силы не работают на всех виртуальных перемещениях, поэтому нижняя точка есть положение равновесия маятника.
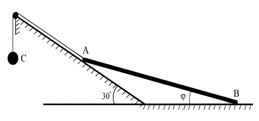 Пример 2. Система состоит из однородного тонкого стержня АВ с массой М и груза D с массой m, соединенного со стержнем невесомой нитью. При гладкости плоскостей консервативная система с одной степенью свободы имеет идеальные связи. При произвольных массах тел в системе нет положений равновесия. Но если
Пример 2. Система состоит из однородного тонкого стержня АВ с массой М и груза D с массой m, соединенного со стержнем невесомой нитью. При гладкости плоскостей консервативная система с одной степенью свободы имеет идеальные связи. При произвольных массах тел в системе нет положений равновесия. Но если 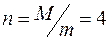 , то все положения системы, допустимые связями
, то все положения системы, допустимые связями 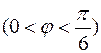 , есть безразличные положения равновесия. Это видно из принципа виртуальных перемещений, который можно записать в следующем виде:
, есть безразличные положения равновесия. Это видно из принципа виртуальных перемещений, который можно записать в следующем виде:
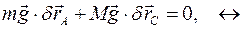
:
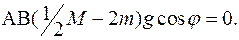
Консервативные системы с циклическими координатами.
Определение. Обобщенная координата 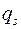 , которая не содержится в функции Лагранжа
, которая не содержится в функции Лагранжа 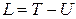 , то есть
, то есть 
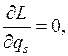
называется циклической координатой.
Если консервативная система не имеет циклических координат, то положения равновесия системы изолированы (локальны). В системах с циклическими координатами имеются множества безразличных положений равновесия, которые не являются изолированными.
Изолированные положения равновесия обладают тем свойством, что в них система может находиться в покое, то есть при нулевых начальных условиях, на некотором конечном интервале времени движение отсутствует.