Операционное исчисление.
Преобразования Лапласа и его свойства
Определение: преобразованием Лапласа называется преобразование  , где t – действительное переменное, а
, где t – действительное переменное, а 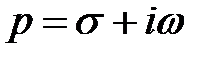 – комплексное переменное.
– комплексное переменное.
Функция 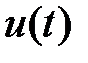 называется оригиналом, а
называется оригиналом, а 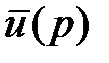 – изображением.
– изображением.
Приведем примеры вычисления изображений для некоторых оригиналов
1. 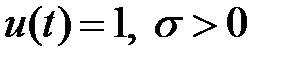 , то
, то 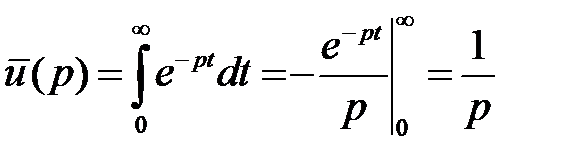 ;
;
2.  , то
, то 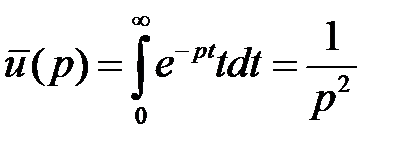 (интегрируя по частям);
(интегрируя по частям);
3.  – целое положительное число, то
– целое положительное число, то 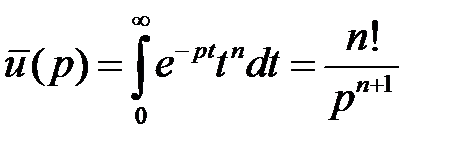 (интегрируя
(интегрируя 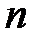 раз по частям).
раз по частям).
4.  , то
, то  .
.
В дальнейшем будем считать, что оригинал 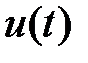 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1. 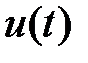 является кусочно-непрерывной и кусочно-гладкой функцией (т.е.
является кусочно-непрерывной и кусочно-гладкой функцией (т.е. 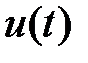 и ее производная на каждом конечном отрезке имеют не более конечного числа точек разрыва и притом только первого рода);
и ее производная на каждом конечном отрезке имеют не более конечного числа точек разрыва и притом только первого рода);
2. 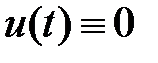 при
при  ;
;
3. с возрастанием  модуль функции
модуль функции 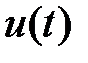 растет не быстрее некоторой показательной функции; точнее
растет не быстрее некоторой показательной функции; точнее  , где
, где 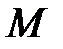 и
и  – постоянные.
– постоянные.
Условие (3) обеспечивает абсолютную сходимость интеграла  , где
, где 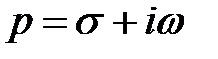 при
при  т.е. для всех точек
т.е. для всех точек  , лежащих правее прямой
, лежащих правее прямой 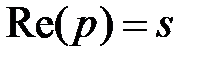 . Действительно, если
. Действительно, если  , то
, то 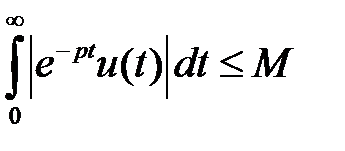
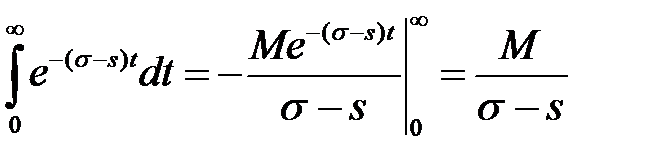 . В дальнейшем будем всюду предполагать, что
. В дальнейшем будем всюду предполагать, что 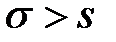 .
.
Докажем несколько свойств преобразования Лапласа.
1.  .
.
Доказательство: 
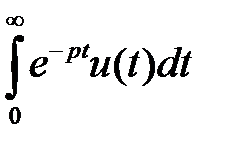
 .
.
2. 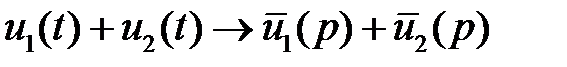 .
.
Доказательство: 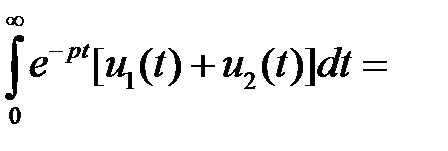
 +
+ 
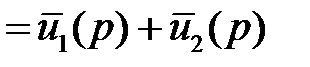 .
.
Следствие из свойств (1) и (2) 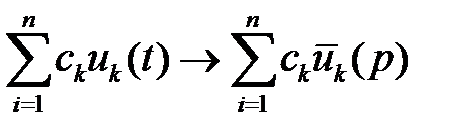 .
.
3.  . В частности, если
. В частности, если 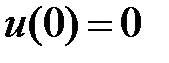 , то
, то
дифференцирование оригинала сводится к умножению изображения на 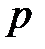 .
.
Доказательство: 
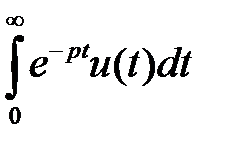
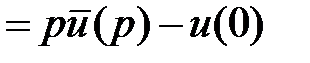 ; равенство получается интегрированием по частям при этом
; равенство получается интегрированием по частям при этом  . Применяя свойство (3) два раза получим
. Применяя свойство (3) два раза получим 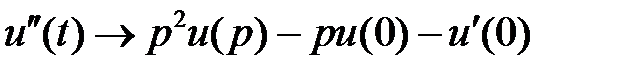 . Применяя свойство (3)
. Применяя свойство (3) 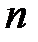 раз получим
раз получим  .
.
4. интегрированию оригинала соответствует деление изображения на  .
. 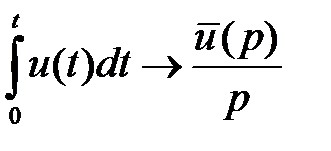 .
.
5. Теорема запаздывания.
Сдвигу функции  в направлении оси
в направлении оси  на отрезок
на отрезок 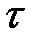 соответствует умножение изображения на
соответствует умножение изображения на 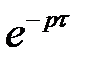 :
:  .
.
Доказательство: 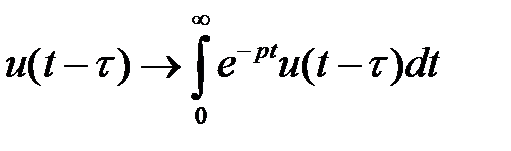 выполним подстановку
выполним подстановку  т.к.
т.к.  при
при  , то
, то 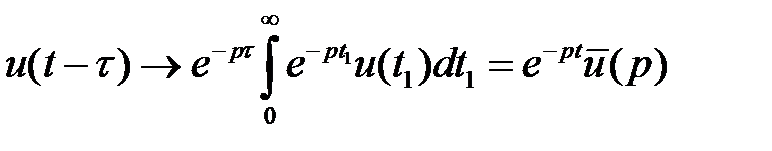 .
.
6. Теорема подобия
 .
.
Доказательство: 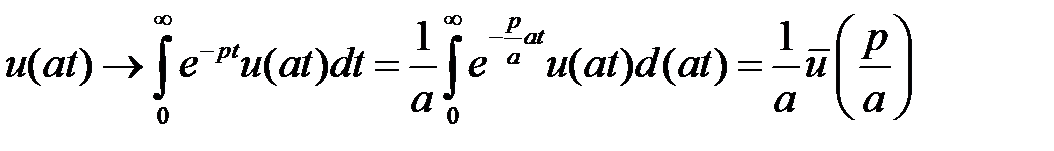 .
.
7. Теорема смещения  (
(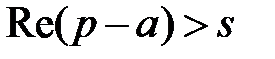 ).
).
Доказательство: 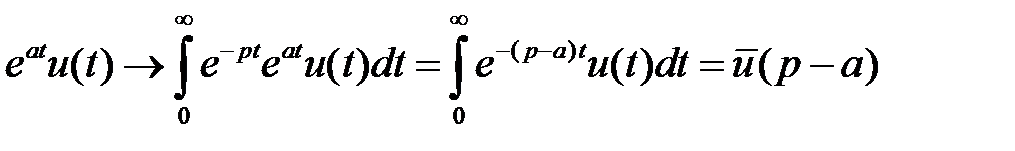 .
.
Составим таблицу перехода от оригинала к изображению и обратно
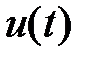
| 
|
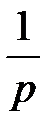
| |
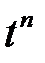 
| 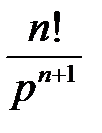
|
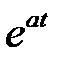
| 
|
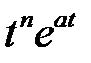
| 
|
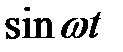
| 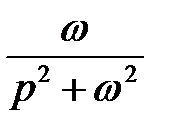
|
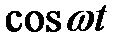
| 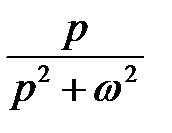
|
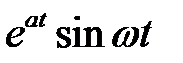
| 
|

| 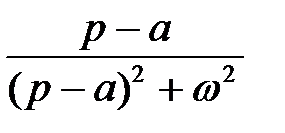
|
Следующие свойства.
8. Дифференцирование изображения.
Дифференцирование изображения сводится к умножению оригинала на (–t). 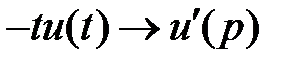 .
.
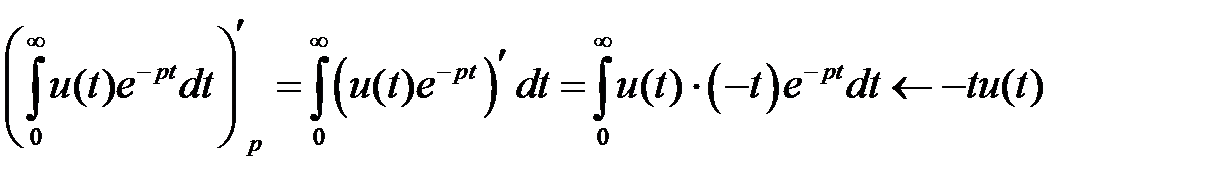
9. Интегрирование изображения.
Если 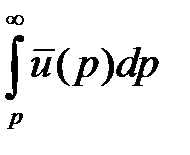 сходится, то он служит изображением функции
сходится, то он служит изображением функции 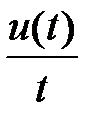 .
.
Доказательство: Если функция  такова, что
такова, что  при
при 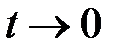 , то
, то 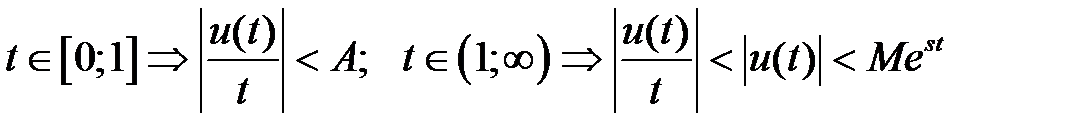 т.е. функция
т.е. функция 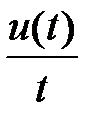 имеет изображение. Тогда
имеет изображение. Тогда 
 . Т.е.
. Т.е.  .
.
10. Теорема умножения. Теорема о свертке.
Сверткой двух функций действительного переменного  и
и 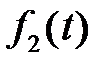 называется третья функция
называется третья функция  . Совершая в интеграле замену переменной
. Совершая в интеграле замену переменной  , получим
, получим
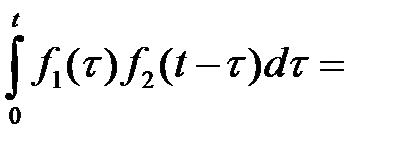
 . Таким образом, от перестановки функций их свертка не меняется.
. Таким образом, от перестановки функций их свертка не меняется.
Теорема: изображением свертки двух оригиналов служит произведение их изображений.
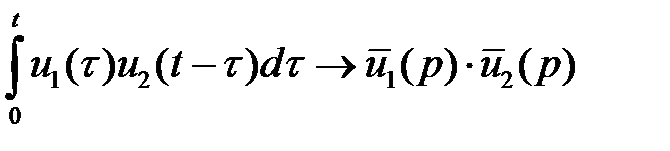 .
.
11. Изображение периодической функции.
Пусть функция  периодическая функция с периодом
периодическая функция с периодом  (при
(при  ). Введем вспомогательную функцию
). Введем вспомогательную функцию 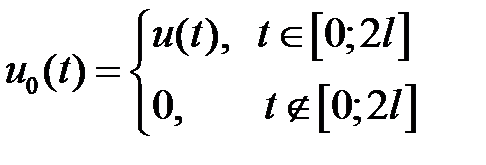
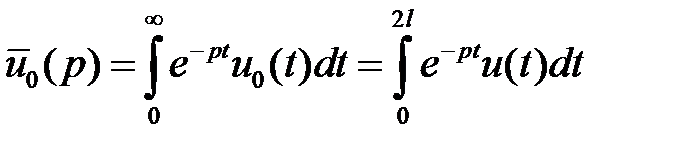 . Но функция
. Но функция  , причем
, причем  – та же периодическая функция, но с запаздыванием на один период и
– та же периодическая функция, но с запаздыванием на один период и  . Тогда
. Тогда 
Решение дифференциальных уравнений операционным методом.
Пусть дано дифференциальное уравнение 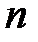 – прядка
– прядка  с начальными условиями
с начальными условиями  .
.
Тогда 
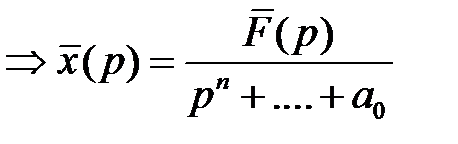 . Раскладывая полученную дробь в сумму простейших и выполняя обратный переход по таблице, получаем решение дифференциального уравнения.
. Раскладывая полученную дробь в сумму простейших и выполняя обратный переход по таблице, получаем решение дифференциального уравнения.
Если не все начальные условия  равны 0, то выполним преобразования с основной формулой преобразования Лапласа.
равны 0, то выполним преобразования с основной формулой преобразования Лапласа.
Пример 1. Найти изображение периодической функции
 , где
, где  – период функции.
– период функции.
Решение. Изображение функции 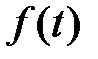 найдем по формуле изображения периодической функции
найдем по формуле изображения периодической функции 

Пример 2. Найти оригинал функции  по известному изображению
по известному изображению 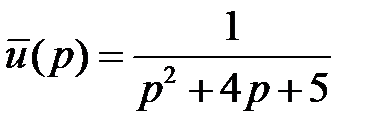 .
.
Решение. Выделим полный квадрат в знаменателе дроби и воспользуемся таблицей перехода  .
.
Пример 3. Решить дифференциальное уравнение, удовлетворяющее данным начальным условиям.
 .
.
Решение. Пусть функция  имеет изображение
имеет изображение  . Тогда
. Тогда  ,
,  ,
,  . Проведем преобразование дифференциального уравнения и получим
. Проведем преобразование дифференциального уравнения и получим 

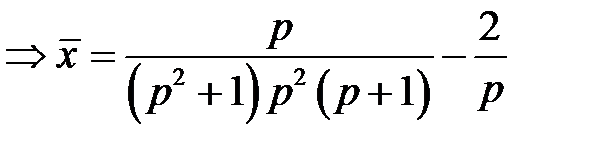 . Разложим дробь
. Разложим дробь  в сумму простейших
в сумму простейших  . Выполнив необходимые преобразования получим
. Выполнив необходимые преобразования получим 
 . Следовательно
. Следовательно  выполнив переход от изображений к оригиналам найдем решение дифференциального уравнения
выполнив переход от изображений к оригиналам найдем решение дифференциального уравнения 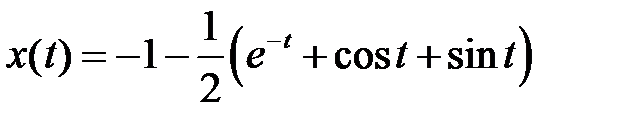 .
.