Закрытый ключ.
4. Вычисляется значение b=axmodp – комбинация (a, p, b) представляет собой открытый ключ получателя.
На этапе шифрования:
1. Отправитель генерирует произвольное случайное число y (0<y<p).
2. Помещает в начале шифрограммы число (aymodp).
3. Вычисляет величину k = (by mod p) = ((ax mod p)y mod p).
4. Используя некоторую, заранее оговоренную в данной реализации, часть k в качестве симметричного ключа для любого блочного шифра шифрует отправляемое сообщение.
5. Надежно стирает числа y и k из оперативной памяти и других мест, куда они могли случайно попасть.
На этапе дешифрования:
1. По приходу зашифрованного сообщения получатель отделяет от пакета величину (aymodp) и вычисляет на ее основе ((ay modp)xmodp) – математика доказывает, что полученное число будет равно тому самому k, которое вычислил отправитель, так как в данной формуле операндыxиyможно менять местами.
2. Выделив из k туже самую часть, что и отправитель, получатель дешифрует весь идущий далее пакет симметричным алгоритмом.
Схема алгоритма Эль Гамаль приведена на рис. 3.2.
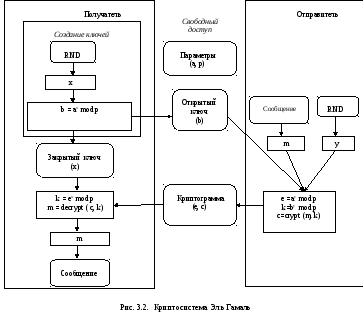
Проблема дискретного логарифма состоит в том, что, зная основание степени и получившийся после возведения результат по модулю простого числа, невозможно за обозримое время определить, в какую именно степень было возведено основание. В схеме Эль Гамаль потенциальный злоумышленник может получить значения a, p, (axmod p) и (aymod p).
!!! ОЧЕНЬ ВАЖНО!Однако из-за сложности определения чисел х и y "в чистом виде" у него не оказывается возможности вычислить значение k = (axymod p), которое так необходимо для прочтения шифровки.
По криптостойкости с схеме Эль Гамаль 512-битное число p приравнивается к 56-битному симметричному ключу, размер которого в настоящее время недостаточен для надежного шифрования. Поэтому на практике применяются р длиной в 768, 1024 и 1536 бит.
Пример 3. В качестве простого числа, порождающего циклическую группу, выберем р = 11, за образующий элемент примем число а = 7 (при возведении 7 в степень 1, 2, 3 и т. д. по модулю 11 последовательно проходят все 10 значений [7, 5, 2, 3, 10, 4, 6, 9, 8, 1]). Секретным ключом х выберем 6, параметрbпринимает значениеb= (axmodp) = (76mod11) = 4. В целом ключ принимает вид (а = 7, р = 11, b = 4).
Предположим, что некий абонент хочет передать сообщение. Он выбрал случайное число, не превосходящее р, например, у = 9. В начало шифрограммы помещается число (aymodp) = 79mod11) = 8. Кроме того, на основе у и открытого ключа отправитель вычисляет k = bymodp= 49 mod11 = 3. Выбрав значение 3 или какие-либо его биты в качестве симметричного ключа, отправитель шифрует передаваемые данные и стирает величины 9 и 3 со своих накопителей.
Получатель по приходу пакета для вычисления k = (aymodp)xmodp возводит число 8 из заголовка шифрограммы в степень секретного ключа и получает k = 86mod11 = 3 – то же самое значение, которое использовал отправитель, шифруя собственно данные.
Схемы на основе эллиптических кривых(СХОДСТВО С ШИФРОМ Эль Гамаля)
Асимметричное шифрование, использующее эллиптические кривые, не является отдельной схемой. Она представляет собой модификацию других схем, увеличивающую скорость работы алгоритмов и одновременно уменьшающую размеры ключей. Асимметричная криптография на эллиптических кривых очень похожа на проблему дискретного логарифма. В связи с этим асимметричная криптография на эллиптических кривых больше всего напоминает криптосистему Эль Гамаль.
Эллиптической кривой, используемой в данной схеме, является выражение вида у2= (х2+ а´х + b) mod p, гдеp– большое простое число. Обе координаты х и у, а также параметры а и b являются натуральными числами из диапазона [0; p-1], т. е. все вычисления производятся по модулю р. Пары чисел (х, у) удовлетворяющие приведенному равенству называются точками эллиптической кривой.
Над точками определена операция сложения следующим образом. Если абсциссы точек Q1(х1, y1) иQ2(х2,у2) различимы, то точка S =Q1+Q2имеет координаты (хs,ys), определяемые формулами:
k = ((y2 – y1) / (х2 – х1)) mod p
xs = (k2 – x1 – x2) mod p
ys = (k ´ (x1-x2) – e1) mod p.
Если же точкиQ1иQ2совпадают, т. е. речь идет о об "удвоении точки" то применяются следующие формулы:
k = ((3 ´ x 12 + a) / (2 ´ y1)) mod p
xs = k2 – 2´ x1) mod p
ys = (k ´ (x1 – xs) – y1) mod p.
Подобные формулы позволяют ввести над точками эллиптической кривой операцию умножения на число: R =n´P–nкратное сложение точкиP с самой собой. Данная операция по свойствам тождественна операции возведения в степень в конечном поле простого числа. Само умножение (шифрование) характеризуется полиномиальной(временная сложность алгоритма) скоростью вычислений, а вот попытка по известным P и R определить число n уже не укладывается в полиномиальные рамки.
Вот более короткое объяснение метода Эль Гамаля:
Схема шифрования Эль Гамаля. Алгоритм шифрования Эль Гамаля основан на применении больших чисел для генерации открытого и закрытого ключа, криптостойкость же обусловлена сложностью вычисления дискретных логарифмов.
Последовательность действий пользователя:
1. Получатель сообщения выбирает два больших числа P и G, причем P > G.
25. Получатель выбирает секретный ключ - случайное целое число X < P.
26. Вычисляется открытый ключ Y = G x mod P.
27. Получатель выбирает целое число K, 1< K< P -1.
28. Шифрование сообщения (M): a = GK P, b = Y K M mod P, где пара чисел (a, b) является шифротекстом.