Как разделить многочлен на двучлен.

Корни многочлена

Корнем многочлена 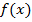называется число 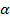, такое, что 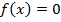, т.е.

.

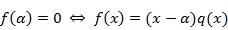Число 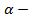k -кратный корень многочлена 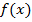, если

.

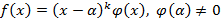При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. Здесь мы рассмотрим, каким образом это сделать проще всего.

Теорема Безу утверждает, что остаток от деления многочлена 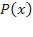на двучл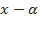ен равен .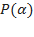

Но для нас важна не сама теорема, а следствие из нее:

Если число является корнем многочлена 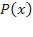, то многочлен 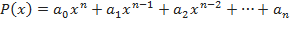делится без остатка на двучлен .

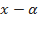Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на 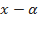, где – корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.

Эта задача распадается на две: как найти корень многочлена, и как разделить многочлен на двучлен.

Остановимся подробнее на этих моментах.

Как найти корень многочлена.

Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.

Здесь нам помогут такие факты:

Если сумма всех коэффициентов многочлена равна нулю, то число1является корнем многочлена.

Например, в многочлене 3 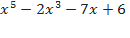сумма коэффициентов равна нулю: 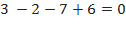. Легко проверить, что 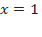является корнем многочлена.

Если сумма коэффициентов многочлена при четных степенях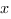равна сумме коэффициентов при нечетных степенях, то число-1является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку 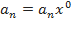, а 0– четное число.

Например, в многочлене 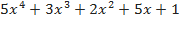сумма коэффициентов при четных степенях : 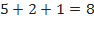и сумма коэффициентов при нечетных степенях : 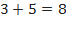. Легко проверить, что 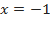является корнем многочлена.

Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.

Для приведенного многочлена степени 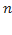(то есть многочлена, в котором старший коэффициент – коэффициент при 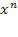– равен единице) справедлива формула Виета:

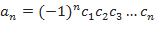, где 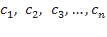– корни многочлена .

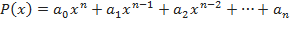Есть еще формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.

Из этой формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.

Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.

Рассмотрим, например, многочлен .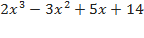

Делители свободного члена: .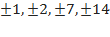

Сумма всех коэффициентов многочлена равна 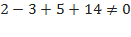следовательно, число 1 не является корнем многочлена.

Сумма коэффициентов при четных степенях : -3-14=-17

Сумма коэффициентов при нечетных степенях : 2+5=7

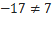, следовательно, число -1 также не является корнем многочлена.

Проверим, является ли число 2 корнем многочлена: 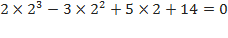, следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен 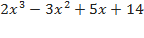делится без остатка на двучлен .

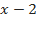Как разделить многочлен на двучлен.

Многочлен можно разделить на двучлен столбиком.

Разделим многочлен 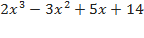на двучлен 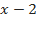столбиком: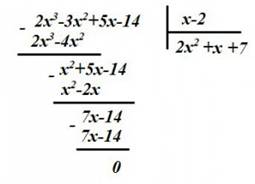

Есть и другой способ деления многочлена на двучлен – схема Горнера.

Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на ее месте пишем 0 – так же, как при составлении таблицы для схемы Горнера.

Итак, если нам нужно разделить многочлен 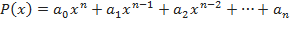на двучлен 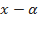и в результате деления мы получаем многочлен 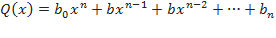, то коэффициенты многочлена 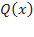мы можем найти по схеме Горнера:

Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число является корнем многочлена 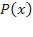, то остаток от деления многочлена на 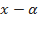равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.

Используя схему Горнера, мы «убиваем двух зайцев»: одновременно проверяем, является ли число корнем многочлена 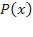и делим этот многочлен на двучлен .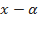