Гипербола и её уравнение.

Уравнения линии. Кривые 2-го порядка

Уравнение линии.

Уравнением линии называется уравнение с двумя переменными х и у, которому удовлетворяют координаты любой точки, принадлежащей этой линии, и не удовлетворяют координаты любой точки, не принадлежащей этой линии.

Отсюда следующие правила для решения задач.

Правило 1.

Чтобы определить принадлежит точка линии или нет, достаточно подставить её координаты в заданное уравнение. Если получится верное равенство, значит точка принадлежит линии, если неверное, то – не принадлежит.

Правило 2.

Чтобы найти точки пересечения нескольких линий достаточно решить систему уравнений, задающих эти линии.

Прямая на плоскости.

1. 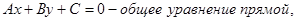угловой коэффициент находится по формуле:

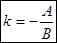
2.

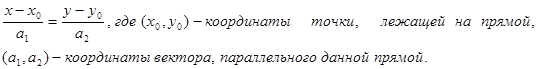
3.

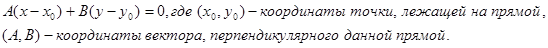
4. y=kx+b, где k - угловой коэффициент прямой, b-начальная ордината,

5. y-y₀=k(x-x₀) - уравнение «пучка» прямых,

6.

 

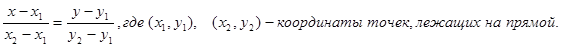
Условия параллельности и перпендикулярности двух прямых

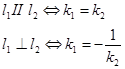
Две прямые перпендикулярны тогда и только тогда, когда угловые коэффициенты этих прямых обратны по величине и противоположны по знаку.

Две прямые параллельны тогда и только тогда, когда угловые коэффициенты этих прямых равны между собой.

 

Задача 1.

Указать, какая пара уравнений соответствует перпендикулярным прямым.

1. 2х+3у-7=0, 3х-2у=0,

2. 5х-2у+1=0, 4х+10у-1=0,

3. 6х-4у+7=0, 8х-12у-1=0

Решение:

Найдём угловые коэффициенты данных прямых и сравним их:

1. k1=-2/3, k2=3/2, k1=-1/k2, значит прямые перпендикулярны.

2. k1=5/2, k2=-4/10=-2/5, k1=-1/k2, значит прямые перпендикулярны.

3. k1=6/4=3/2, k2=8/12=2/3, k1¹-1/k2, значит прямые не перпендикулярны.

 

Задача 2.

Указать, какая пара уравнений соответствует параллельным прямым.

1. 2х-3у-7=0, 6х-9у+1=0,

2. 6х-3у+1=0, 2х+5у+5=0,

3. 6х-4у+7=0, 12х-8у-1=0

Решение:

Найдём угловые коэффициенты данных прямых и сравним их:

1. k1=2/3, k2=6/9=2/3, k1=k2, значит прямые параллельны.

2. k1=2, k2=-4/10=-2/5, k1¹k2, значит прямые не параллельны.

3. k1=6/4=3/2, k2=12/8=3/2, k1=k2, значит прямые параллельны.

 

Задача 3.

Составить уравнение прямой, проходящей через точку А(3;-2) и имеющей направляющий вектор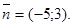

Решение:

1. Выбираем точку М(х,у)Îl.

2. Найдём вектор .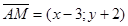

3. Направляющий вектор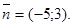

4. Запишем уравнение прямой 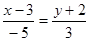, откуда 3х-9=-5у-10, 3х+5у+1=0 – искомое уравнение.

Задача 4.

Даны вершины треугольникам А(-2,1), В(4,-3), С(-3,5). Составить уравнение:

- высоты, опущенной из вершины В на сторону АС;

- медианы, проведённой из вершины С;

- стороны АВ.

Решение:

Имеем: -1(х-4)+4(у+3)=0, или –x+4+4у+12=0, или х-4у-16=0 - уравнение высоты ВК.

2. Чтобы составить уравнение медианы СР, найдём координаты точки Р:

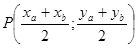
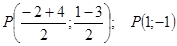
Воспользуемся уравнением прямой, проходящей через две точки:

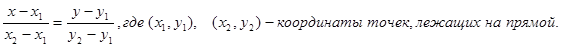
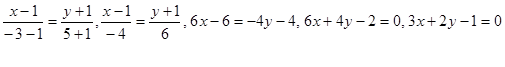
Итак, 3х+2у-1=0 - уравнение медианы СР.

3. Чтобы написать уравнение стороны АВ, воспользуемся той же формулой.

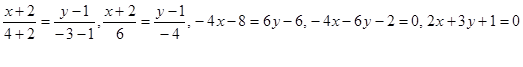
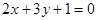- уравнение стороны АВ.

Вопросы и упражнения для самоконтроля:

1. Что называется уравнением линии на плоскости?

2. Как определить принадлежит точка линии или нет?

3. Как найти точку пересечения нескольких линий?

4. Составьте уравнения прямых, параллельных осям координат и проходящих через точку К(-3,4).

5. Даны вершины треугольника А(1,-3), В(5,-1),С(-3,5). Составьте уравнение:

а) стороны АВ;

б) медианы, проведенной из вершины В;

в) высоты, опущенной из вершины С на сторону АВ.

6. Даны точки А(-5,3) и В(-7,-1). Составьте уравнение прямой, проходящей через точку С(1,-2) параллельно АВ.

7. Даны координаты вершин параллелограмма АВСК: А(-1,2), В(-2,-2), С(5,-2). Составьте уравнение его диагоналей АС и ВК.

8. Что называется уравнением линии на плоскости?

9. Напишите уравнение осей координат и прямых, па­раллельных им.

10. Какова схема составления уравнения прямой?

11. Используя схему, составьте уравнения прямой в зависимости от способа ее задания.

12. Дайте определение нормального вектора, направляющего вектора и углового коэффициента прямой.

13. Сформулируйте условия параллельности и перпендикулярности двух прямых.

14. Напишите формулы для вычисления угла между двумя прямыми.

15. Как найти точку пересечения двух прямых?

16. Составьте уравнения прямых, проходящих через точку К ( -3,4) параллельно осям координат.

17. Даны вершины треугольника А(1,-3), В(5,-1),С (-3,5). Составьте уравнение:

а) стороны АВ;

б) медианы, проведенной из вершины В;

в) высоты, опущен­ной из вершины С на сторону АВ.

18. Даны точки А(-5,3) и В(-7,-1). Составьте уравнение прямой, проходящей через точку С(1,-2) параллельно АВ.

19. Какую ординату имеет точка С(-1,у ), лежащая на той же прямой, что и точки А(-5, 2) и В ( -3, -1)?

20. Даны координаты трех вершин параллелограмма АВСК: А(11, 2), В (-2,-2), С (5,-2). Составьте уравнение его диагоналей АС и ВК.

Ответы: 9. х+3=0, у-4=0, 10. а) х-2у-7=0; б) х+Зу-2=0; в) 2х+у+1=0.

11. 2х-у-4=0. 12. С(-1,-4). 13. 2х+3у-4=0; х-2у-2=0.

Решить задачи самостоятельно:

В треугольнике АВС написать уравнение:

- стороны АВ,

- медианы ВМ,

- прямой, проходящей через точку В, параллельно прямой АС,

- высоты ВD.

	А	В	С
	(4,-5)	(-1,2)	(0,8)
	(3,5)	(-2,9)	(1,6)
	(-5,1)	(7,-4)	(3,-2)
	(6,-2)	(-1,8)	(-1,2)
	(3,-2)	(4,-3)	(-1,0)
	(0,-7)	(4,-5)	(-3,9)
	(7,-4)	(0,-4)	(2,-6)
	(-1,2)	(6,-2)	(-4,7)
	(-1,0)	(-5,1)	(4,-5)
	(-1,8)	(0,8)	(4,-3)

Окружность и эллипс.

Окружностью называется замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Расстояние от любой точки окружности P(x,y) до ее центра называется радиусом. Центр окружности и сама окружность лежат в одной и той же плоскости. Уравнение окружности радиуса R с центром в начале координат (каноническое уравнение окружности) имеет вид x²+y²=R²

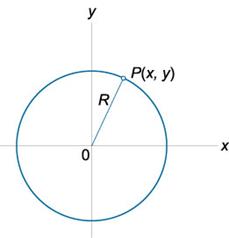
Уравнение окружности радиуса R с центром в произвольной точке A(a,b) записывается (x−a)²+(y−b)²=R²

Эллипс - это кривая, которая имеет уравнение 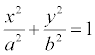. Это каноническое уравнение эллипса, в нем координатные оси совпадают с осями эллипса.

Он имеет два фокуса. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

Чертеж эллипса

1.

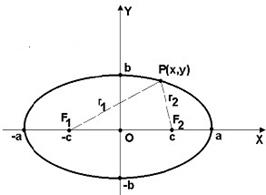
F₁, F₂ – фокусы. F₁ = (c; 0); F ₂ (- c; 0)

с – половина расстояния между фокусами; a – большая полуось;

b – малая полуось; r₁ и r₂ - фокальные радиусы.

Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси. Эксцентриситет обозначается буквой e:

Если а>b, то e=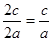

Если а<b, то e=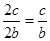

Так как по определению 2а>2c, то эксцентриситет эллипса всегда выражается правильной дробью, т. е. 0£e£1.Эксцентриситет характеризует форму эллипса.

Рассмотрим два основных случая расположения эллипса относительно осей координат.

 

Показатели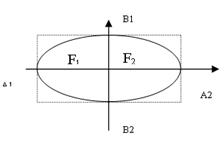
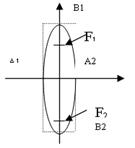
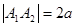
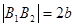
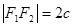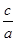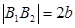
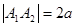
Положение фокусов Координаты фокусов Соотношение между а и b Большая ось   Малая ось   Фокусное расстояние   Эксцентриситет     Соотношение между a,b,c.	F1,F2ÎOx F1(-с,0),F2(с,0)   a>b   e=   a2-b2=c2	F1,F2ÎOy F1(0,с),F2(0,-с)   a<b   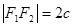e= 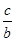  b2 -a2=c2

 

Задача 1.

Найти координаты фокусов, длины осей, эксцентриситет эллипса, заданного уравнением 2x²+y²=32.

Решение:

Приведём уравнение эллипса к каноническому виду. Для этого разделим все его члены на 32:

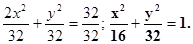
Мы видим, что а²=16, b²=32, откуда, а=4, b=4 .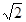

Так как b>a, то фокусы эллипса расположены на оси ординат.

Они имеют координаты F₁(0,с),F₂(0,-с), где с определяется из соотношения b² -a²=c²

Подставив в него значения а и b, получим 32-16=с², с=4. Итак, фокусами эллипса служат точки F₁(0,4),F₂(0,-4).

Далее находим: большую ось эллипса 2b=8 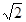; малую ось 2а=8; эксцентриситет e= 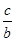@0,705.

Задача 2.

Составить каноническое уравнение эллипса, у которого малая ось равна 6, а расстояние между фокусами 8.

Решение:

Т. к. малая ось равна 6, то фокусы расположены на оси Ox. Имеем b=3, с=4. из соотношения a²-b²=c² находим а: a²-9=16, откуда а²=9+16=25, а=5.

Итак, каноническое уравнение эллипса имеет вид:

.

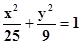Задача 3.

Доказать, что уравнение 36x²+100y²-3600=0 является уравнением эллипса. Найти координаты фокусов и фокальное расстояние.

Решение:

Перенесём 3600 в правую часть уравнения и разделим на 3600, получим:

.

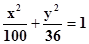Это уравнение является уравнением эллипса.

Из равенства a²-b²=c² следует, что с=8. Фокусы эллипса находятся в точках F₁(-8,0),F₂(8,0). Фокальное расстояние .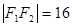

Задача 4.

Написать каноническое уравнение эллипса, проходящего через точку М(5;0), если фокальное расстояние равно 6.

Решение:

Т.к. фокальное расстояние равно 6, то с=3. Запишем каноническое уравнение эллипса:

.

По условию точка М(5,0) принадлежит эллипсу, значит её координаты удовлетворяют данному уравнению, т. е.:

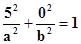, откуда а²=25, а=5.

Из равенства a²-b²=c² находим b²=16,b=4.

Искомое уравнение эллипса будет иметь вид:

.

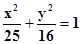Гипербола и её уравнение.

Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек (называемых фокусами) есть величина постоянная, меньшая, чем расстояние между этими точками.

Фокусы гиперболы принято обозначать буквами F₁ и F₂, расстояние между фокусами - через 2с, разность расстояний от любой точки гиперболы до фокусов - через 2а(2а<2с).

Каноническое уравнение Гиперболы имеет вид:

 

,

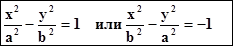где a,b,c связаны между собой равенством:

a²+b²=c²

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине действительной оси.

Эксцентриситет обозначается буквой e:

Если а>b, то e=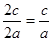

Если а<b, то e=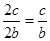

Так как по определению 2а<2c, то эксцентриситет эллипса всегда выражается неправильной дробью, т. е. e>1.Эксцентриситет характеризует форму гиперболы.

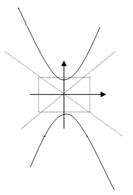
Рассмотрим два основных случая расположения гиперболы относительно осей координат.

Показатели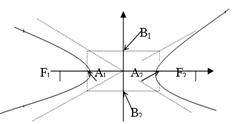
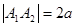
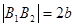
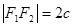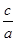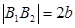
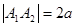
Положение фокусов Координаты фокусов   Действительная ось   Мнимая ось   Фокусное расстояние   Эксцентриситет     Соотношение между a,b,c.	F1,F2ÎOx F1(-с,0),F2(с,0)     e=   с2-а2=b2	F1,F2ÎOy F1(0,с),F2(0,-с)   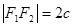  e= 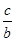  с2 -b2=а2
Уравнение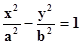

 

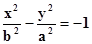
Асимптоты гиперболы имеют уравнения y=±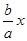

Задача 1.

Составить простейшее уравнение гиперболы, если расстояние между её фокусами равно 40,а между её вершинами равно 30.

Решение:

По условию 2а=30, т. е. а=15; 2с=40, т. е. с=20.

Т.к. a²+b²=c² , то b²=c²-a²=400-225=175.

Следовательно .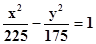

Задача 2.

Действительная полуось гиперболы равна 8, эксцентриситет равен 1,5. Составить уравнение гиперболы.

Решение:

По условию а=8, т.е. а²=64, e=с/а=1,5, откуда с=1,5*8=12, с²=144, значит, b²=с²-а²=144-64=80.

Следовательно,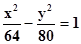

Задача 3.

Составить уравнение гиперболы, проходящей через точки .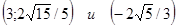

Решение:

Уравнение гиперболы можно записать так: x²b²-y²a²=a²b². Подставим вместо x и y координаты заданных точек, получим систему уравнений:

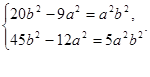
Умножим первое уравнение на 4, а второе уравнение на –3 и сложим оба уравнения, тогда получим а²=5. Подставим а²=5 в первое уравнение, находим b²=3. Следовательно, 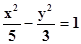- искомое уравнение.

Задача 4.

Даны фокусы гиперболы F₁(-10;0) и F₂(10;0) и её асимптота 4х+3у=0. Написать уравнение гиперболы.

Решение:

Запишем уравнение асимптоты в виде y=-4/3x, находим отношение полуосей гиперболы b/a=4/3. Из условия задачи следует, что с=10. Поэтому a²+b²=100.

Задача свелась к решению системы уравнений:

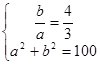
Подставляя b=4/3а во второе уравнение системы, получаем .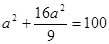

Откуда а²=36. Теперь находим b²=(4/3 а)²=16/9*36=64.

Следовательно, гипербола имеет уравнение 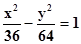.