Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

(5)

где р, q — некоторые действительные числа, - некоторая функция. Если , то уравнение

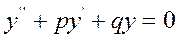(6)

называется однородным. В противном случае, т.е. при 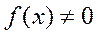, уравнение (5) называется неоднородным.

Рассмотрим сначала решение линейного однородного уравнения (6) с постоянными коэффициентами.

Напомним, что линейной комбинацией функций у₁(х) и у₂(х) с коэффициентами С₁ и С₂ называется выражение вида C₁у₁(х) + C₂у₂(х). Если линейная комбинация функций C₁у₁(х) + C₂у₂(х) равна нулевой функции только тогда, когда коэффициенты C₁ и С₂ равны нулю, то функции у₁ и у₂ называются линейно независимыми, в противном случае — линейно зависимыми.

Пример 1. Убедиться в линейной независимости следующих функций:

а) и , где λ₁ ≠ λ₂

б) и

в) и , где β ≠ 0.

Решение. а) Если C₁ + C₂ ≡ 0, то C₁ ≡ - C₂ , но так как λ₁ ≠ λ₂, то функция, стоящая в правой части последнего равенства, является постоянной, только если C₂ = 0 и, следовательно, C₁ = 0.

б) Тождественное равенство C₁ + C₂ ≡ 0 возможно, только если функция C₁ + С₂х является нулевой, откуда следует C₁ = С₂ = 0.

в) Предположим, что C₁ 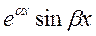+ С₂ 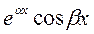≡ 0. Тогда 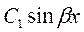+ ≡ 0. Если хотя бы один из коэффициентов C₁ или С₂ отличен от нуля, то нетрудно подобрать такое значение переменной х, что функция в левой части последнего равенства отлична от нуля (например, x = 0 или x = ). Поскольку это невозможно, то C₁ = С₂ = 0

Исследовать линейную независимость функций удобнее с помощью определителя Вронского:

Говоря о решениях уравнения (6), отметим прежде всего, что они обладают структурой линейного пространства: если у₁ (х) и у₂ (х) — решения уравнения (6), то их линейная комбинация

у = C₁ у₁ + С₂ у₂, (7)

где C₁ и С₂ некоторые числа, также является решением этого уравнения.

Другими словами, формула (7) задает способ построения новых решений уравнения (6) из уже имеющихся. Возникает вопрос: сколько и какие решения уравнения (6) следует задать, чтобы с их помощью можно было описать все решения этого уравнения? Ответ на него дает следующая теорема.

Теорема 1. Если у₁ (х) и у₂ (х) — линейно независимые частные решения уравнения (6), то общее решение этого уравнения является линейной комбинацией этих частных решений, т.е. имеет вид (7) для некоторых постоянных действительных чисел C₁ и С₂.

Итак, чтобы найти общее решение уравнения (6), достаточно знать два его частных решения у₁ и у₂.

Будем искать решение уравнения (6) в форме у = 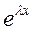, где λ — некоторое действительное число. Так как

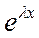() " + р ( 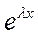)' + q = (λ² +р λ +q) ,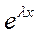

то эта функция является решением уравнения (6), если число λ есть корень уравнения

λ² +р λ + q = 0, (8)

которое называется характеристическим уравнением исходного однородного уравнения (6).

Описание решений однородного ЛДУ2 зависит от того, какие корни имеет характеристическое уравнение (8) в зависимости от дискриминанта. Справедлива теорема.

Теорема 2. Пусть характеристическое уравнение (8) однородного уравнения (6) имеет действительные корни λ₁ и λ₂, причем λ₁ ≠ λ₂. Тогда общее решение уравнения (6) имеет вид

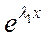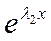у= C₁ + C₂ , (9)

где C₁ и С₂ — некоторые числа.

2. Если характеристическое уравнение (8) имеет один корень λ (кратности 2), то общее решение уравнения (6) имеет вид

у= C₁ + C₂ , (10)

где C₁ и С₂ — некоторые числа.

3. Если характеристическое уравнение (8) не имеет действительных корней, а имеет комплексно сопряженные корни, то общее решение уравнения (6) имеет вид

у = C₁ 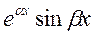+ С₂ , (11)

где α = - р/2, β = , C₁, С₂ — некоторые числа.

Принимая во внимание теорему 1 и результаты, полученные в примере, для доказательства достаточно проверить, что функции, линейные комбинации которых рассматриваются в п. а, б, в, действительно являются решениями уравнения (6) при сделанных предположениях.

Пример 2. Найти частное решение следующих уравнений при указанных начальных условиях:

а) y" – 3y' + 2y = 0, у (0) = 3, y' (0) = 4;

б) y" – 2y' + y = 0, у (0) = 1, y' (0) = 0;

в) y" – 2y' + 2y = 0, у (0) = 1, y' (0) = 1.

Решение. а) Решая характеристическое уравнение λ² – 3 λ + 2 = 0, находим его корни λ ₁ = 1, λ ₂ = 2. Тогда общее решение данного уравнения имеет вид

у= C₁ + C₂ .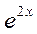

Найдем такие значения постоянных C₁ и С₂, при которых выполняются заданные начальные условия. Так как у (0) = C₁ + С₂ и y' (0) = C₁ + +2 С₂, то постоянные C₁ и С₂ находим, решая систему

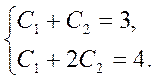
Откуда C₁ = 2, С₂ = 1.

По теореме о существовании и единственности решения уравнения вида (6) найденное частное решение у = 2е^х + е^2х — искомое.

б) Решая характеристическое уравнение λ² – 2 λ + 1 = 0, получаем λ ₁ = λ ₂ ^:= 1. Согласно п. 2 теоремы 2 общее решение дифференциального уравнения (6) имеет вид

у = (C₁ + С₂х) е^х.

Так как у (0) = 1, то C₁ = l и, поскольку y' = у + С₂е^х и у (0) = 0, то С₂ = - 1. Таким образом, окончательно получаем частное решение

у = (1 – х) е^х.

в) Характеристическое уравнение λ² – 2λ + 2 = 0 не имеет действительных корней. В этом случае согласно п. 3 теоремы 2 общее решение дифференциального уравнения имеет вид

y = C_l e^x sin x + C₂ e^x cos х (α = β = 1).

Так как у (0) = 1, то С₂ = 1. Найдем y' = (C₁ – С₂) e^x sin х + (C₁ + С₂) е^х cos х. Учитывая, что у' (0) = 1, получим C₁ = 0. Таким образом, приходим к частному решению

у = е^х cos х

 

Перейдем теперь к решению линейного неоднородного уравнения (5) с постоянными коэффициентами.

Это уравнение может быть в частности решено методом вариации произвольных постоянных, который состоит в следующем. Сначала находится общее решение у = C₁у₁ + С₂у₂ однородного уравнения (6), имеющего ту же левую часть, что и исходное неоднородное уравнение (5). Затем решение неоднородного уравнения (5) находится в виде

y = C₁ (x) у₁ + С₂ (х) у₂,

т.е. предполагается, что постоянные C₁ и С₂ являются функциями независимой переменной х. При этом функции C₁ (x) и С₂ (х) могут быть найдены как решения системы

(12)

 

Пример 3. Решить уравнение

у" – 3у + 2у = е^х. (13)

Решение. Решая соответствующее однородное уравнение

у" – 3у' + 2у = 0 (14)

находим

у = C₁ е^х + С₂ е^2х.

Полагая теперь, что C₁ и С₂ — функции переменной х, найдем первые производные этих функций. Решая систему (12)

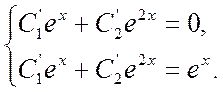
находим

Полученные дифференциальные уравнения – это уравнения с разделяющимися переменными. Решая эти уравнения, получаем

C₁ = - х + С₃, С₂ = - е^-х + С₄,

где С₃, С ₄ — некоторые постоянные. Таким образом, окончательно решение уравнения имеет вид

у = (- х + С₃) е^х + (- е^-х + С ₄ ) е^2х

или

y= С₃ е^х + С ₄ е^2х + (- х – 1) е^х.

 

Обратим внимание на структуру полученного решения. Первые два слагаемых — это общее решение однородного уравнения, соответствующего исходному дифференциальному уравнению. Последнее слагаемое, как нетрудно убедиться непосредственным вычислением, - это частное решение исходного уравнения. Аналогичное утверждение справедливо и в общем случае, т.е. справедлива теорема.

Теорема 3. Общее решение линейного неоднородного дифференциального уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения

Следует отметить, что метод вариации произвольных постоянных достаточно сложен, поэтому в ряде случаев целесообразно использовать другие методы решения, основанные на теореме 3. Сначала, как и при методе вариации произвольных постоянных, находится общее решение однородного дифференциального уравнения, а затем отыскивается частное решение неоднородного уравнения. При этом вид частного решения устанавливается по виду правой части уравнения и задача сводится к отысканию коэффициентов этого частного решения.

 

УПРАЖНЕНИЯ

Составить дифференциальные уравнения семейств кривых:

1. у = Сх².

2. у² = 2 Сх.

3. х³ = С (х² – у²).

4. у = С₁ е^2х + С₂ е^-х.

Решить дифференциальные уравнения с разделяющимися переменными:

1. ху' – у = у³.

2. у – ху ' = (1 + х²у ' ).

3. ху у' = 1 – х².

4. ху dx + (х + 1) dу = 0.

5. = xy dy.

6. 2х² уу ' + у² = 2.

7. у у ' + х = 1.

8. у ' = 10 ^х+у.

Решить уравнения, используя замену переменной:

1. у ' – у = 2х – 3.

2. (2x – y) dx + (4x – 2y + 3) dy = 0.

Решить однородные дифференциальные уравнения:

1. у = .

2. (х-у) у dx – x² dy = 0.

3. (x² + y²) dx – 2xy dy = 0.

4. у dx + dy = 0.

5. у dy + (x – 2y) dx = 0.

6. y = x (y ' – ).

Решить линейные уравнения первого порядка:

1. .

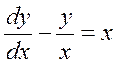2. у' + 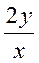= х³.

3. y² dx – (2ху + 3) dy = 0.

4. y' – y = e^x.

Решить уравнения, используя понижение порядка:

1. y''' = е^2х.

2. х (у'' + 1) + у' = 0.

Найти частные решения уравнений, удовлетворяющие начальным условиям:

1. (у"х – у') = х³, у (1) = 1, у' (1) = 0.

2. 2у (у')² + у" = 0, у (0) = 0, у' (0) = - 3.

Решить линейные однородные уравнения:

1. у" – 5у' + 6у = 0.

2. у" + 2y' + y = 0.

3. у' – у = 3у".

4. у" + 4у' + 3у = 0.

Решить линейные уравнения:

1. у" – 4 у' + 4у = х².

2. у" + 2у' + у = е^2х.

3. у" – 8у' + 7у = 14.

4. у" – 4у = е^х.

Найти решения уравнений, удовлетворяющие начальным условиям:

1. у" – 2у' + у = 0, у (2) = 1, у' (2) = - 2.

2. у" + у = 4е^х, у (0) = 4, у' (0) = - 3.

3. у" – 2у' = 2е^х, у (1) = - 1, у' (1) = 0.

4. у" + 2у' + 2у = хе^-х, y (0) = у' (0) = 0.

5. За 30 дней распалось 50% первоначального количества радиоактивного вещества. Через сколько времени останется 1% первоначального количества?

Указание. Использовать закон радиоактивного распада: количество радиоактивного вещества, распадающегося за единицу времени, пропорционально количеству вещества, имеющегося в рассматриваемый момент.

 

 

Занимательная задача. Из точки в норку по некоторой траектории ползет жучок со скоростью . Заметив жучка, одновременно из точки вылетает птичка со скоростью 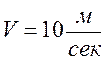. Соответствующие размеры даны на рисунке.

 

 

Успеет ли жучок заползти в норку?