Перевод
Thermodynamics of Negative Pressures in Liquids
(Термодинамика отрицательных давлений в жидкостях)
A. Imre1, K. Martinas2, L. R N. Rebelo3
1- НИИ Атомной энергии Венгрии, 2‑ Ф-т атомной энергии Будапештского Университета Этвёша, Венгрия,
3 ‑ Химический ф-т Лиссабонского ГУ, Португалия
АННОТАЦИЯ
Природа использует отрицательное давление наиболее изобретательными и эффективными способами. Тем не менее, частью научного сообщества состояния отрицательного давления по-прежнему считаются невозможными. В настоящей работе мы покажем, что любая конденсированная фаза может существовать в режимах абсолютного отрицательного давления, в то время как для газовых фаз это не так. Мы также демонстрируем, что такие состояния не только просто возможны, но и, несмотря на их метастабильность, во многих случаях наблюдались экспериментально. Более того, уже оказываются определенными физические свойства ряда веществ и растворов, находящихся в растянутой жидкой фазе при абсолютных отрицательных давлениях. Тем не менее, постижение и достижение успеха в эксперименте, вызывающем высокое напряжение в жидкости, оказывается довольно затруднительным. Так, уравнения состояния и компьютерное моделирование являются ключевыми инструментами для изучения метастабильных жидкостей. С помощью простого уравнения состояния мы показываем, как можно добиться режимов: отрицательного давления; максимального внутреннего напряжения, в котором можно удерживать жидкость; и температура, ниже которой жидкость может быть найдена в этом состоянии. Рассмотрены экспериментальные и теоретические работы по жидкостям с отрицательным давлением. Кроме того, демонстрируются сходства и различия между отрицательной температурой и состояниями отрицательного давления. Из-за нетривиального поведения свойств <жидкой> воды, а также ее технологического и научного значения, она была наиболее изученным веществом в метастабильных явлениях. Таким образом, мы будем уделять особое внимание некоторым из богатых особенностей ее метастабильной фазовой диаграммы. Вода относится к классу веществ, которые представляют аномалии плотности. Мы также показываем, как область отрицательного давления фазовой диаграммы оказывается первостепенной в понимании необычного поведения веществ того же <что и вода> класса.
ВВЕДЕНИЕ
Можно встретить физические величины, ‑ такие как масса, объем, длина, ‑ которые не могут принимать отрицательные значения, в то время как другие могут быть как отрицательными, так и положительными (например, электрический заряд, ускорение и т.д.). Однако в некоторых случаях ситуация не столь ясна. Рассмотрим, например, два интенсивных термодинамических свойства: температуру и давление. Со старших классов школы знают, что существует абсолютная (Кельвиновская) шкала температур, при которой она всегда является положительной величиной. При этом, существуют расширенные исследования, в которых выявлена возможность достижения абсолютных отрицательных температур. Хотя нет явных учений о подобных масштабах давления, представляется вполне «естественным», что давление должно быть положительным. Наиболее часто используемой концепцией давления является молекулярно-кинетическая теория газовой фазы [1]: согласно ей давление создается столкновениями частиц со стенками контейнера, что приводит к данному выводу. Частицы прижимаются к стене и, следовательно, давление, безусловно, положительное. Более того, нулевое давление представляет собой абсолютный вакуум, «большое ничто», за которым ничего не может существовать. Поэтому существует общая и неявная связь между давлением и плотностью. Однако это суждение оказывается не универсальным.
Врачи используют термин «отрицательное давление», когда описывают давление легких. Инженеры и исследователи также часто используют этот термин. Такое отрицательное давление, конечно, относится к атмосферному. В этом смысле можно сказать, что давление всегда положительное, а «отрицательное» давление просто означает такое, которое находится в промежутке от нуля до атмосферного давления.
Это, однако, не наш случай. Мы демонстрируем использование теоретических аргументов и экспериментальных данных, а также показываем, что любая конденсированная (твердая или жидкая) фаза может существовать в режимах абсолютного отрицательного давления, в то время как для газовых фаз это не так. Другими словами, хотя в газовой фазе давление и плотность прямо пропорциональны, в конденсированных фазах эта пропорциональность возникает не обязательно.
Чтобы обсуждать режимы отрицательных давлений в жидкостях (или твердых телах), удобно распространить общее определение давления. В жидкостях и твердых телах давление должно рассматриваться как 3×3-тензор (P), а не как скаляр [2]. В наиболее распространенном случае (газы, гидростатическое давление и т.д.) все диагональные элементы равны (р), а недиагональные (которые описывают механический сдвиг) равны нулю и, следовательно, давление (р) равно 1/3×Тr(P), где Tr(P) обозначает след матрицы тензора P:
В твердых телах отрицательное давление можно легко интерпретировать как механическое напряжение. Например, растягивание карандаша с площадью поперечного сечения 1 см2 с использованием силы 20 N вдоль оси x, приведет к элементу pxx тензора давления -0,1 МПа (с учетом +0,1 МПа, возникающего из-за атмосферного давления). Такое же действие по всем осям (x, y и z) приведет к изотропному напряжению, т.е. к отрицательному давлению p = 1/3Tr(P) = -0,1 МПа.
Та же концепция может быть применена и к жидкостям. Разница заключается в том, что они требуют гораздо большей аккуратности для преуспевания в эксперименте с «растянутой» жидкостью.
ЭКСПЕРИМЕНТАЛЬНЫЕ НАБЛЮДЕНИЯ ОТРИЦАТЕЛЬНОГО ДАВЛЕНИЯ В ЖИДКОСТЯХ
Более 300 лет назад (1663) Гюйгенс, Бойль, Папен и другие провели несколько экспериментов во время встречи Королевского общества (Лондон) [3]. Они использовали стеклянные трубки с одним концом, которые были заполнены ртутью сверху. Открытый конец погружали в сосуд с ртутью. Когда трубку <из почти горизонтального положения> поднимали <вертикально> (открытый конец оставался под ртутью), ртутный столб не обрушался. Торричелли выполнял аналогичный эксперимент за три десятилетия до этого. При этом, если в опыте Торричелли с трубкой последняя давала только около 760 мм (27-28 дюймов) высоты вакуумированной с верхней части ртутного столба, Гюйгенс и др. (1663) смогли полностью заполнить трубы высотой около 2 метров (75 дюймов).
Это было сделано без повышения внешнего давления и достигнуто без разрушения ртутной колонны*. Таким образом, они произвели отрицательные давления (называемые механическими напряжениями или напряженными жидкостями) в верхней части ртутной колонны (выше точки А, рис. 1). В настоящее время этот эксперимент можно легко объяснить: адгезия между стеклянной стенкой и жидкостью удерживает ртуть, при условии, что силы притяжения в самой ртути (когезия) также достаточны для поддержания этого отрицательного давления в верхней части колонны. В то время об адгезии и когезии ничего не было известно, поэтому они не представили никаких объяснений эксперимента.
Рис. 1. Эксперименты Торричелли (A) и Гюйгенса (B). Высота h 1 представляет собой высоту жидкой ртутной колонны, которая находится в равновесии с внешним атмосферным давлением и с вакуумом (точнее, с давлением паров ртути при комнатной температуре, p = 0,5 Па). В случае опыта Гюйгенса трубка полностью заполнена жидкостью, и поэтому жидкость находится под механическим напряжением в любой точке выше h 1. Если высота h 2 достаточно велика, верхняя часть колонны находится под отрицательным давлением. Градиент давления в эксперименте Гюйгенса строится в части (C).
* Чтобы объяснить разницу между результатами Гюйгенса и Торричелли, мы должны принять во внимание, что ‑ как показали позднее ‑ любые крошечные пузырьки между жидкостью и стеклом или любые загрязнения могут приводить к падению ртутного столба.
Кроме того, эксперимент «не работал» воспроизводимо должным образом – иногда столбец ртути обрушался до высоты Торричелли (испытывал коллапс).
Существует два различных механизма, посредством которых метастабильная жидкость, находящаяся под механическим напряжением разрушается (релаксирует) до своего устойчивого состояния (либо до газового состояния, либо до состояния, равновесия между жидкостью и газом в зависимости от наложенных внешних связей: в первом случае налагаются переменные p и T, в то время как в втором - V и Т). Одним из механизмов является гетерогенное зарождение пузырьков газа на границе раздела жидкость-контейнер или взвешенные в жидкости частицы (адгезия), а другим – гомогенное зарождение внутри основной части жидкой фазы (когезия). Последний <механизм> отражает максимально возможное на практике внутреннее механическое напряжение, которое жидкость может выдержать до разрушения и, таким образом, является характеристикой данной жидкости; первый же <механизм> зависит от организации эксперимента. Этот <механизм>, связанный с адгезией, зависит от качественных и количественных характеристик стенок контейнера и/или примесей в образце и, следовательно, трудно воспроизводится. Помимо этих практических пределов устойчивости, которые индуцируются кинетически, можно найти абсолютный предел устойчивости (спинодаль), который определяется термодинамикой. Спинодаль растянутой чистой жидкости отражает, таким образом, максимальное абсолютное внутреннее механическое напряжение, которое жидкость может выдержать до разрушения (механическая нестабильность). В смесях спинодаль представляет собой источник, который относится к нестабильности вещества (в отношении образования новой фазы переменного состава), поскольку здесь эта неустойчивость материала будет происходить на более преждевременной метастабильной стадии, чем механическая нестабильность.
Тем не менее, с экспериментальной точки зрения, это говорит о том, что для того, чтобы успешно генерировать очень высокие (по модулю) отрицательные давления в жидкости (предпочтительно – в сильно связанной жидкости), следует использовать чрезвычайно малые количества образца, где и площадь контакта, и вероятность существования включений примесей резко минимизирована. Так, Zheng и др. [4] смогли получить величину около -1400 атм в ультрачистых образцах воды массой около 10-9 г.
Это был, пожалуй, <случай, когда> сочетание отсутствия объяснения и невоспроизводимость ранних экспериментов заставляли забывать их на века. В середине и конце девятнадцатого века Донни и, независимо, Рейнольдс, вновь открыли явление [5]. И, хотя эксперимент Торричелли преподается даже в средних школах, эти эксперименты мало кто знает.
С тех пор были разработаны несколько методов [5-22] для создания отрицательных давлений в жидкостях. Достижимое отрицательное давление может составлять даже несколько сотен МПа [4, 23]. Динамические методы, основанные на внезапном вытягивании или ультразвуковом излучении, создают отрицательное давление в течение очень короткого периода времени. Статические методы способны генерировать и удерживать давление в течение более длительных периодов (даже в течение многих дней) [5, 18]. Почти все методы производят анизотропное давление; тензор давления может иметь ненулевые недиагональные элементы, и даже диагональные могут различаться между собой. И это не то же самое, что однородное давление в термодинамике.
Изотропное <отрицательное> давление производится методом Бертло, изобретенным М. Бертло в 1850-х годах. Метод основан на термическом сжатии жидкости при ее адгезии к стенкам контейнера. Этот метод не только генерирует действительно изотропное, однородное давление, но оно удерживает его в течение значительного промежутка времени. Метод, объясняемый ниже, показано на рис. 2.
<Для постановки эксперимента необходимо> сначала заполнить тонкую трубку холодной жидкостью под вакуумом, а затем запаять ее пламенем. Хотя капилляр почти заполнен, после отпайки останется небольшой пузырек. (А). По мере увеличения температуры пузырек газа становится все меньше и меньше, поскольку тепловое расширение жидкости больше, чем расширение стеклянной трубки. При определенной и хорошо воспроизводимой температуре (так называемая температура заполнения) он исчезает (B). При этой температуре давление будет еще равно равновесному давлению паров. Дальнейшее повышение температуры будет одновременно увеличивать давление вдоль квази-изобары (квази-изохоры? – прим. пер.) в жидкой фазе (С). Эта стадия называется стадией предварительного сжатия. Чем выше положительное давление, тем выше полученное потом отрицательное давление. Это связано с тем, что высокое предварительное сжатие способствует исчезновению захваченных газовых пузырьков в щелях стенок и способствует диффузии растворенных в жидкости газов. Еще более эффективный подход [21, 22] использует много циклов повышения и сброса давления.
Рис. 2: Схематическое представление метода Бертело (подробное описание см. В тексте). (A): при температуре T 1 жидкость находится под давлением насыщенного пара, pv: p = pv (T). “Белая” область представляет собой газовую фазу; (B): при более высоких температурах (T fill) жидкость полностью заполняет контейнер и p = pv (T fill). (С): Для еще более высоких температур (T 2) жидкость расширяется по квази-изохоре
.
Стрелки представляют собой давление, оказываемое на стенки. (D): при охлаждении и после прохождения температуры T fill (например, до температуры T 3 < T fill), жидкость начинает испытывать растяжение, а соответствующее давление
Жидкость «прилипает» к стенам. При достаточно низких температурах давление уже отрицательно. (Е): Зарождение газовых пузырьков (белых кружков) неизбежно произойдет при температуре T break < T 3,
____________________________________________________________________________
На этом и последующих этапах давление можно контролировать, измеряя деформацию стенок, или же его можно оценить, если известна фактическая температура и термо-барический коэффициент жидкости:
где 
‑ коэффициент теплового расширения и изотермическая сжимаемость соответственно.
На следующем шаге температура медленно снижается. в конечном итоге снова достигается температура заполнения (T fill). Если жидкость характеризуется хорошей адгезией к стенкам, то при уменьшении температуры газовые пузырьки не образуются. Жидкость теперь находится в возбужденном (метастабильном) состоянии.
Дальнейшее охлаждение (в случае без наблюдения кавитации) приведет в конечном итоге к ситуации (D), где p < 0. Поскольку жидкость «погружается» все больше и больше в область отрицательного давления, ее метастабильность становится все более критической. Поэтому в какой-то момент происходит коллапс с образованием пузырьков газа, что обычно сопровождается металлическим звуком (звук щелчка). Жидкость расслаивается до состояния с давлением, равным давлению пара при данной температуре (E).
Этот эксперимент настолько прост, что его можно выполнять практически в любой лаборатории, оборудованной газо-кислородной горелкой, вакуумным насосом, жидким азотом или сухим льдом (для замораживания жидкости при отпайке) и термостатом. Во время процедуры наполнения в случае воды, ее следует использовать при температуре 4 °C, где обеспечивается ее максимальную плотность. Поскольку большинство жидкостей имеют тепловой коэффициент порядка 1 МПа/К (при комнатной температуре), следует быть осторожным, чтобы избежать перегрева, так как увеличение на 10 К может вызвать повышение давления на 10 МПа (рис. 2 в). Доступное отрицательное давление с использованием дегазированных и фильтрованных жидкостей обычно имеет порядок нескольких МПа. В этом диапазоне давлений жидкость является глубоко метастабильной и, таким образом, может коллапсировать при любых воздействиях. Любая вибрация, трение, твердофазные загрязнения или маленькие пузырьки могут вызвать этот коллапс, называемый кавитацией (из-за газовых полостей, т.е. пузырьков, в жидкости). Те же причины могут привести к коллапсу перегретых жидкостей. Перегрев и растяжение – близкие вещи (см. ниже, а также рис. 3).
И так же, как каждое твердое тело обладает максимальной величиной механического напряжения, при котором конкретное твердое тело обязательно разрушается, жидкости также имеют температурно-зависимый практический предел устойчивости, называемый пределом гомогенной нуклеации [5, 24-26]. Эта граница может быть предсказана кинетической теорией нуклеации, и это произойдет при достижении абсолютного теоретического предела устойчивости. Последнее является термодинамическим пределом (мета) устойчивости, спинодалью (см. ниже, рис.3 и рис.5), при котором сжимаемость, тепловое расширение и теплоемкость расходятся до бесконечности для чистой жидкости. Для смесей (растворов) эти функции остаются конечными в спинодали (всестороннее обсуждение критериев устойчивости можно найти в [26-29]), за исключением особого случая возникновения азеотропии (при азеотропном составе смесь <ведет себя> как чистая жидкость).
Измерение отрицательного давления довольно сложно, но не безнадежно. Несколько методов измерения положительного давления могут быть адаптированы к отрицательным давлениям. Например, изготовление трубки Бертло в форме спирали [18] позволяет измерять давление через деформацию этой спирали (как, например, в спиральных манометрах Бурдона) ‑ независимо от того, является ли это давление положительным или отрицательным. Аналогично, тензодатчик, прикрепленный к стенке ячейки [21], может обнаруживать деформацию этой стенки (именно так работают новые электрические манометры для измерения обычного положительного давления) что, таким образом, позволяет рассчитывать отрицательное давление по сигналу электрического напряжения.
Исследования поведения жидкостей при отрицательном давлении начались с Бертло. Он был первым, кто систематически наблюдал способность жидкости (а именно воды) поддерживать механическое напряжение <растяжения>. Максимальные пределы натяжения жидкостей по большей части далеко не достигнуты. Это связано с тем, что гетерогенное зарождение происходит намного раньше, чем гомогенное зарождение, что, в свою очередь, происходит раньше, чем достигается спинодальный предел. Именно последнее связано с максимальной абсолютной прочностью на растяжение, при которой можно удерживать жидкость. Начиная с Бертло, большинство исследований отрицательного давления было сделано о практическом пределе гетерогенного зарождения.
В большинстве случаев этот предел составляет около десятков МПа. Исключение составляет вода. Zengh et al. [4] были в состоянии экспериментально достичь около -150 МПа, значение, которое, как полагают, очень близко к максимальной воде десятилетия, может выдержать [24, 25]. Было исследовано несколько других жидкостей [30], таких как этанол, бензол, ксилол, и достигнутое самое глубокое натяжение было около -20 МПа. Даже жидкий гелий может поддерживать <давление> до почти -1 МПа [31, 32].
Считается, что это значение является внутренним пределом сцепления или предельной прочности на растяжение, поскольку оно было получено [33] путем экстраполяции на отрицательные режимы функций состояния (? – исх.: response function) (например, скорость звука), когда жидкий гелий приближается к критическому состоянию – линия спинодали. Здесь, как и вблизи критической точки, функции состояния (?), такие как сжимаемость, тепловое расширение и теплоемкость, уходят в бесконечность (скорость звука уменьшается до нуля), и, таким образом, теоретически звуковые экстраполяции до нулевого значения скорости звука позволяют провести строгую оценку максимальной внутренней сплошности чистой жидкости. Эксперименты сосредоточены на явлениях, отличных от предела зародышеобразования. К ним относятся: влияние отрицательного давления на кристаллизацию [34-36]; сжимаемость минеральных масел под давлением [13]; сдвиг температуры плавления [20] и положение локуса максимальной плотности воды [19]; структура фосфолипидной суспензии [37]; и фазовый переход «жидкость - жидкость» в растворах полимеров при отрицательном давлении [38-40].
Экспериментальные исследования отрицательного давления были особенно важны в двух модельных случаях: при выяснении фазовой диаграммы воды (включая перегретые и переохлаждаемые метастабильные области) и при исследовании возможности индуцирования разделения фаз в растворах (например, системы полистирол/пропионитрил C2H5CN) путем их растяжения до отрицательных величин давления. Как и ожидалось, в обоих случаях было показано, что физико-химические свойства изменяются плавно и непрерывно, когда пересекается линия р = 0.
Фазовая диаграмма воды была широко изучена (последние подробные обсуждения см., например, [26, 41-46]). Для метастабильных состояний ситуация еще далека от решения. Henderson and Speedy [19, 20] внесли свой первостепенный экспериментальный вклад и показали, как температура плавления воды ведет себя при отрицательных давлениях и как линия максимальной плотности распространяется на эту область. В обоих случаях экспериментальные результаты были получены механические напряжения, <соответствующие давлению> приблизительно -25 МПа. Например, при p = -228 атм нормальная вода плавится при температуре 1,66 ° C, а тяжелая вода – при 4,87 ° C при p = -145 бар. С другой стороны, вода и тяжелая вода предварительно перенаправляли температуру максимальной плотности (TMD) для давления -250 бар 8.5 и 15.0 ° C. Эти результаты и другие данные о расхождении (уходе в бесконечность) функций состояния (? - response) при переохлаждении [47-49] были использованы для поддержки одного из возможных сценариев метастабильной воды. Это так называемый ретроградный (retracing) сценарий спинодали [24, 25], где спинодаль жидкости ограничивает растянутую перегретую и переохлажденную воду. Были предложены два других сценария, также согласующиеся с этими экспериментами: фазовая диаграмма с двумя критическими точками [41, 45, 46] и бессингулярный сценарий [43, 50, 51], где локус максимальной плотности восстанавливается (до положительного наклона) при достаточном отрицательном давлении в бессингулярной интерпретации.
Одна (из возможных) упрощенная фазовая диаграмма для воды может быть изображена на рис. 3. Она основана на вышеупомянутой гипотезе о скоростном состоянии Speedy, которая предсказывает повторный переход спинодали жидкой фазы в область твердого тела. Обратим внимание на существование монотонной кривой максимальной плотности TMD, которая имеет отрицательный наклон; эта кривая заканчивается в точке пересечения со спинодалью вместе с отрицательно наклонной линией сосуществования твердой и жидкой среды, которая меняет наклон (метастабильная жидкая вода становится менее плотной, чем метастабильная твердая вода) при достаточно высоком отрицательном давлении. На линии TMD коэффициент термического расширения a p равен нулю. При этом a p положителен для более высоких температур и отрицателен для более низких. Также особый интерес представляет заштрихованная область на этом же рисунке. Это соответствует состоянию, когда система одновременно перегрета и переохлаждена [14]. В качестве суб-тройного состояния [52], его давление ниже, чем при метастабильном продолжении кривой кипения при данной температуре (перегретое состояние), а его температура ниже, чем при метастабильном продолжении кривой плавления при данном давлении (переохлажденное состояние). Таким образом, <такое состояние> одновременно неустойчиво относительно твердого тела и газа.
Рис. 3: Примерная p-T фазовая диаграмма воды, включающая метастабильные области. <Изображен> спинодальный сценарий растянутого состояния. Линия M – равновесие «лед I – жидкость». Обратим внимание на предсказанное изменение наклона линии при отрицательных давлениях [20]. SB – линия сублимации (практически совпадает с осью температур при данном масштабе давления). V – линия испарения. TMD – локус температуры максимальной плотности, <эта линия> пересекает в точке, помеченной крестиком линию спинодали S (что далее будет отслежено подробнее). C – критическая точка «жидкость-газ». Пунктирная линия дает качественное представление о поведении жидкости Ван-дер-Ваальса, где спинодаль всегда имеет отрицательный наклон. В области, обозначенной штриховкой, жидкость дважды метастабильна: она одновременно переохлаждена и перегрета.
Экспериментальное наблюдение бинарных систем при отрицательном давлении началось только недавно [38, 39]. p ‑ Τ проекцию жидкофазной диаграммы состояния системы полистирол/пропионитрил можно увидеть на рис. 4. Согласно традиционной точке зрения, эта система имеет две отдельные области (низкую и высокотемпературную), где происходит расслоение жидкости, ‑ и между этими двумя областями существует третья, где система представляет собой однородную жидкость. Расширяя измерения ниже p = 0, мы видим, что двухфазные области вообще не разделены. Это также означает, что можно использовать отрицательное давление, чтобы вызвать разделение фаз в многокомпонентных системах, которые при обычных давлениях были бы полностью смешиваемыми. По этой причине возможны <варианты> технологического применения отрицательного давления.
Pressure, MPa
Рис. 4. Проекция p-T диаграммы состояния системы «полистирол – пропионитрил» в области существования жидкого состояния при положительном и отрицательном давлениях: экспериментальные результаты, полученные методом Бертло для молекулярной массы полистирола 22000 г/моль при содержании полимера 20 масс. % [38]. Внутри огибающей кривой (- ×× -), определяемой экспериментальными данными, система является однородной (1 фаза), в то время как снаружи существуют две жидкие фазы (обогащенная полимером и обедненная им).
(Далее следует текст об отрицательном давлении растительных соков в высоких деревьях. И хотя авторы рассматривают это вопрос критически, я это из перевода вообще убрал. Кому интересно – смотрите оригинал – прим. пер.)
ТЕОРЕТИЧЕСКОЕ РАССМОТРЕНИЕ
Когда Ландау в своей знаменитой теоретической работе [61] упоминает, что состояния с p < 0 могут существовать как ограниченно-стабильные, он, безусловно, говорил об абсолютном давлении. Аксиоматическая термодинамика [62] не может исключать такие состояния [63]. В ядерной физике, в квантовой хромодинамике, также встречается давление как отрицательная величина, хотя и исключительно в некоторых экзотических состояниях ([63] и ссылки на них). В последнее время Debenedetti [26] представил в авторитетной форме концепции и принципы метастабильности, в которой абсолютные режимы отрицательного давления представляют собой частный случай. В следующем материале мы опишем наш подход.
В термодинамике интенсивное величины, такие как давление и температура, могут быть определены как:
, (2 а, 2 б, 3 а, 3 б)
где S, E, V, T и p – энтропия, энергия, объем, температура и давление соответственно.
Для определения энтропии можно использовать несколько подходов. Определение Клаузиуса состоит в том, что:
, (4)
где Q – теплота. Это дает энтропию и температуру в виде
(5)
где S - «обычная» энтропия (измеряемая в Дж/K), T ‑ «обычная» температура, S o и K - константы, которые необходимо определить, а S * и T * ‑ «расширенные» энтропия и температура (можно генерировать целые семейства S * s и T * s, просто выбирая разные константы, каждая из которых способна удовлетворять всем ожидаемым критериям энтропии или температуры). Мы можем получить одну энтропию и одну температуру, просто фиксируя константы. Так, согласно третьему закону термодинамики
(6)
а К определяется температурной шкалой.
В классическом подходе шкала давления исходит от механики. Есть и другие подходы, а именно:
(i) Статистическая физика, где принцип максимальной энтропии определяет энтропию в
форме:
Z = K <2> S + S KiXi + S 0, (7)
где K <2>, Ki и S 0 – константы, которые необходимо определить [64].
(ii) Теория флуктуации определяет только вторую производную энтропийной матрицы,
а именно:
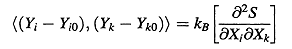. (8)
где Xi,k и Yi,k являются экстенсивными и интенсивными параметрами, которые определяют энтропию в виде:
Z = KS + S KiXi + S 0, (9)
Новые интенсивные параметры такие:
(10)
где величины, отмеченные звездочками, также удовлетворяют всем критериям, ожидаемым для T и p. Поэтому шкалы температуры и давления не фиксированы.
Термодинамика конструктивного анализа (Callen, Tisza) постулирует свойства энтропии следующим образом:
Существует дифференцируемая функция S экстенсивных переменных со свойством:
SA (EA, VA, NA) + SB (EB, VB, NB) < SAB (EAB, VAB, NAB), (11)
где EA + EB = EAB и т.д.
Эти постулаты дают нам энтропию [65], подобную той, которая дается уравнением (9). Вот почему Tisza [66] постулирует отдельно, что <функция> p появляется автоматически. Значения Ki имеют физический смысл, поскольку они определяют местоположение максимальной энтропии. Есть два особых состояния в качестве кандидатов на абсолютный максимум. Первый появляется в относительной, а второй – в абсолютной шкале (см. ниже).
Относительная шкала: относительная шкала используется для систем находящихся в контакте с внешним телом (? – systems in a reservoir). Выбирая константу Κ = -1 и маркируя T 0 и p 0 в качестве температуры и давления внешнего тела (? – systems in a reservoir), получаем:
, (12)
где П – термодинамическое удаление от равновесия, называемое э кс тропией [67]. При этом П³0. Нуль достигается для П, если равновесие достигнуто, в противном случае П строго больше нуля.
Таким образом, шкалы температуры и давления будут относительными (т.е., будет дана разница между величинами системы и резервуара). Следовательно, и соответствующее давление и температура могут быть либо отрицательными, либо положительными, что давление и температура системы могут быть либо выше, либо ниже, чем внешнего тела (? – systems in a reservoir).
Абсолютная шкала. Энтропия имеет максимумы при предельных значениях обширных величин. Существуют два «естественных» предела, а именно те, где Х ® 0 и Х ® ¥. Что касается энергии, то
, (13)
а S - возрастающая функция <внутренней> энергии. Классические физические соображения показывают, что абсолютный максимум энтропии должен принадлежать бесконечной энергии. В том же духе
. (14)
Уравнения (13) и (14) показывают, что ни Т = ¥, ни р = 0 не могут быть достигнуты (при постоянстве N). Эти утверждения согласуются с тремя постулатами термодинамики (все – утверждения отрицания):
I. Вечного мобильного первого типа не существует.
II. Вечного мобильного второго типа не существует.
III Недостижимость T = 0
IV. Недостижимость Т = ¥
V. Недостижимость p = 0
VI. Недостижимость р = ¥
Что касается шестого утверждения, то можно потребовать (доказать) недоступность р = ¥, хотя это не входит в наши планы. Эти шесть утверждений дают нам полное описание замкнутой системы (из-за существования античастиц высказываний о недоступности нулевой точки химического и электрического потенциала не существует).
Отрицательное давление, отрицательная температура
Температура
Эти постулаты приводят к тому, что системы, удовлетворяющие критерию 
, не могут существовать при отрицательной температуре. Однако квантовая природа физического мира допускает появление систем с верхним или нижним пределом плотности энергии. В системах с верхней границей E / V теоретическое препятствие к возникновению отрицательной температуры отсутствует. На самом деле в этом верхнем диапазоне E/V имеются хорошо известные системы, такие как лазеры и ядерные спины. В обоих случаях системы с отрицательными температурами являются фактически подсистемами, встроенными в тело положительной температуры. В то время как температура таких подсистем может быть отрицательной, ничего не известно об их давлении, поскольку объем и давление для этих систем не определены.
Давление
Как и при температурах, постулаты I-V дают в качестве следствия то, что системы, которые удовлетворяют критерию (при постоянстве N), не могут достигать отрицательных давлений и, следовательно, газы не могут находиться под давлением, меньшим нуля. Однако, опять же, системы с верхней границей V / N (т.е. те, которые не могут быть расширены до бесконечного объема). В таких случаях термодинамика не запрещает появление отрицательных давлений. Эти системы, представленные либо жидкостями, либо твердыми веществами, могут выдерживать отрицательное или положительное давление, а их температура всегда положительна. Система с одновременными верхними границами для E/V и V/N пока еще не идентифицирована. Поэтому нет известной реальной системы, в которой давление и температура были бы одновременно отрицательными.
Хотя концепции и принципы, лежащие в основе существования отрицательного давления и отрицательной температуры, схожи, между этими двумя состояниями существуют некоторые важные различия. Хотя отрицательная температура определяется только для подсистем (встроенных в систему с положительной температурой), отрицательное давление может быть определено для всей системы. Состояния с отрицательной температурой не имеют определенного давления, а состояния с отрицательным давлением имеют определенную и измеряемую положительную температуру. Более того, хотя отрицательные температуры выше положительных (их можно достичь, минуя бесконечную температуру), отрицательные давления ниже положительных (т.е., они могут быть достигнуты через нуль). С экспериментальной точки зрения существует также важное различие между ними. Система с отрицательной температурой устойчива в термодинамическом смысле, но только в том случае, если она внедрена в положительную температурную среду. Таким образом, отрицательная температура является неравновесной. Вот почему отрицательные температуры можно удерживать только в течение нескольких минут. Напротив, системы отрицательного давления могут быть изолированы, так что взаимодействие с атмо