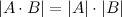Основные источники:
1. Григорьев С.Г., Иволгина С.В. «Математика»: учебник для студ. образоват. учреждений сред.проф. образования под редакцией В.А. Гусева. – 10-е изд., стер. – М.: Издательский центр «Академия», 2014.
Дополнительные источники:
2. Богомолов Н.В., Самойленко П.И. «Математика» учебник для средних спец. учебных заведений -5 изд., переработанное и доп. – М.: издательство Юрайт, 2015.
3. Богомолов Н.В. практические занятия по математике: учебное пособие для СПО / Н.В. Богомолов. – 11-е изд., перераб. И доп. –М.: издательство Юрайт, 2015.
4. Башмаков М.И. Математика. Задачник: учебное пособие для студ. Учреждений сред.проф. образования / М.И. Башмаков. – 4-е изд., стер. – М.: Издательский центр «Академия», 2014г.
Интернет-ресурсы:
1. Федеральное хранилище Единой коллекции цифровых образовательных ресурсов [Электронный ресурс] / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: https://school-collection.edu.ru/catalog/– Загл. с экрана
2. Единое окно доступа к образовательным ресурсам [Электронный ресурс]: каталог образовательных Интернет - ресурсов/ ФГУ ГНИИ ИТТ «Информика». – Электрон.дан. – Режим доступа: https://window.edu.ru/– Загл. с экрана
Раздел 1
«ЛИНЕЙНАЯ АГЛЕБРА»
Система уравнений - это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Решением системы уравнений называется упорядоченный набор чисел - значений неизвестных, при подстановке которых каждое уравнение системы обращается в верное равенство.
Определение
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
Упорядоченный набор значений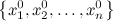 
называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.
Основные понятия и применения
Система может состоять из алгебраических уравнений, линейных алгебраических уравнений, нелинейных уравнений, дифференциальных уравнений.
Методы решения системы уравнений зависят от типа системы. Например, решения систем линейных алгебраических уравнений хорошо известны (метод Крамера, метод Гаусса, матричный метод, метод итераций и т.д.). Для нелинейных же систем общего аналитического решения не найдено, они решаются разного рода численными методами. Аналогично дело обстоит и с системами дифференциальных уравнений.
Системы линейных уравнений широко используются в задачах экономики, физики, химии и других науках.
Матрицы: основные определения и понятия
Определение
Матрицей размера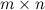 
называется прямоугольная таблица, содержащая 
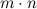чисел, состоящая из 
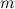строк и 
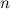столбцов.
Таблица берется либо в круглые скобки, либо окружается двумя параллельными вертикальными прямыми.
Пример
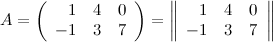
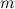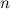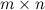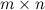Если матрица содержит строк и столбцов, то матрица называется матрицей размера или -матрицей. Размер матрицы указывается справа внизу возле ее имени, либо таблицы с обозначением элементов.
Пример
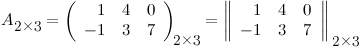
Элементы матрицы
Элементы матрицы 
обозначаются 
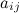, где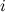 
- номер строки, в которой находится элемент, а 
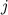- номер столбца.
Пример
Задание. Чему равен элемент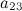 
матрицы 
?
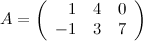Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
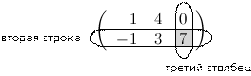
Таким образом,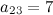 
.
Ответ.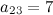
Определение
Строка матрицы называется нулевой, если все ее элементы равны нулю. Если хотя бы один из элементов строки не равен нулю, то строка называется ненулевой.
Замечание. Аналогичное определение и для нулевого и ненулевого столбцов матрицы.
Пример
В матрице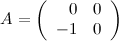 
первая строка является нулевой (любой элемент этой строки равен нулю); вторая строка ненулевая, так как элемент 
.
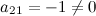Определение
Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний.
Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний.
Пример
Для матрицы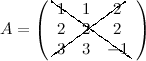 
элементы 1, 2, -1 образуют главную диагональ; а элементы 3, 2, 2 - побочную.
Виды матриц
Определение
Матрица размера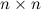 
называется квадратной, число 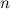называется порядком матрицы.
Пример
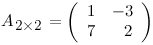- квадратная матрица порядка 2 или матрица второго порядка.
Определение
Матрица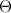 
называется нулевой, если все её элементы равны нулю, т.е. 
.
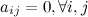Пример
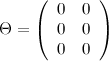
Определение
Матрица, состоящая из одной строки, называется вектор-строкой, а матрица, состоящая из одного столбца, - вектор-столбцом.
Пример
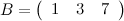- вектор-строка; 
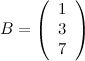- вектор-столбец.
Диагональные матрицы
Определение
Квадратная матрица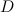 
называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.
Замечание. Диагональные элементы матрицы (т.е. элементы, стоящие на главной диагонали) могут также равняться нулю.
Пример
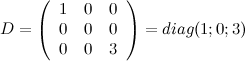
Определение
Единичной матрицей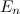 
называется скалярная матрица порядка 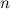, диагональные элементы которой равны 1.
Замечание. Для сокращения записи порядок единичной матрицы можно не писать, тогда единичная матрица обозначается просто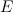 
.
Пример
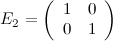- единичная матрица второго порядка.
Треугольные матрицы
Определение
Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.
Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.
Замечание. Диагональная матрица - это пример матрицы, которая является одновременно верхне- и нижнетреугольной.
Пример
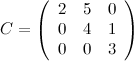- верхнетреугольная матрица.
Операции над матрицами
Некоторые операции над матрицами, такие как сложение и вычитание, допускаются только для матриц одинакового размера
Определение
Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:
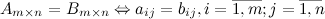
Пример
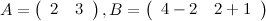. Эти матрицы равны, т.к. равны их размеры: 
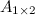и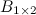 
, а также соответствующие элементы: 
; 
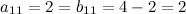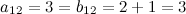
Определение
Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.
Пример
Задание. Пусть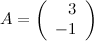 
. Найти матрицу 
.
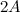Решение.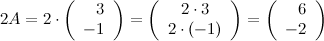 
Ответ.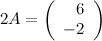 
Определение
Суммой матриц и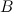 
одного размера называется матрица 
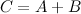такого же размера, получаемая из исходных путем сложения соответствующих элементов.
Пример
Задание. Найти 
, если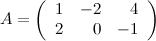 
, 
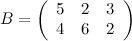
Решение.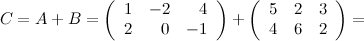 
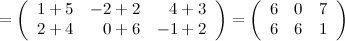
Ответ.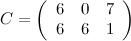 
Операции умножение матрицы на число и сумма матриц называются линейными.
Определение
Произведением матрицы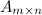 
на матрицу 
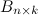называется матрица 
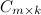такая, что элемент матрицы 
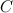, стоящий в 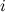-ой строке и 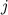-ом столбце, т.е. элемент 
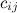, равен сумме произведений элементов 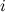-ой строки матрицы на соответствующие элементы 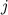-ого столбца матрицы .
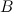Пример
Задание. Найти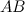 
, если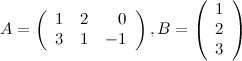 
Решение. Так как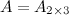 
, а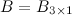 
, то в результате получим матрицу размера 
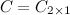, т.е. матрицу вида 
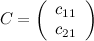. Найдем элементы данной матрицы:
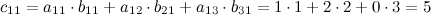
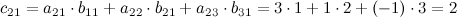
Таким образом, получаем, что:
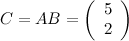
Все вычисления можно было сделать в более компактном виде:
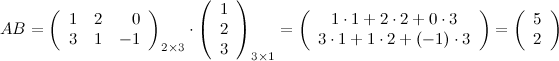
Ответ.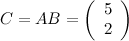
Определение
Транспонирование матрицы - это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.
Пример
Задание. Найти транспонированную матрицу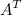 
, если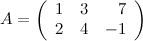 
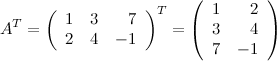Решение.
Определение
Квадратной матрице 
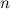-го порядка ставиться в соответствие число 
, называемое определителем матрицы или детерминантом.
Свойства определителей:
Замечание
Все что будет сказано относительно строк, будет относиться и к столбцам.
1° При транспонировании квадратной матрицы её определитель не меняется: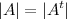 
Пример
Известно, что определитель матрицы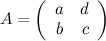 
равен 3. Тогда определитель матрицы 
, которая равна 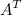, также равен 3.
2° Общий множитель в строке можно выносить за знак определителя.
Пример
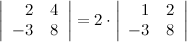
3°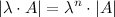 
То есть, если квадратная матрица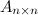 
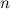-го порядка умножается на некоторое ненулевое число 
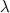, то определитель полученной матрицы равен произведению определителя исходной матрицы на число 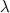в степени, равной порядку матриц.
Пример
Задание. Пусть определитель матрицы третьего порядка равен 3, вычислить определитель матрицы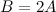 
.
Решение. По свойству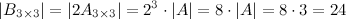 
Ответ.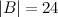 
4° Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.
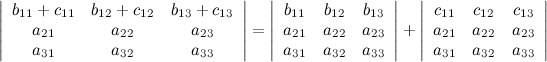
5° Если две строки определителя поменять местами, то определитель поменяет знак.
Пример
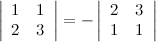
6° Определитель с двумя равными строками равен нулю.
Пример
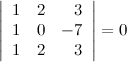
7° Определитель с двумя пропорциональными строками равен нулю.
Пример
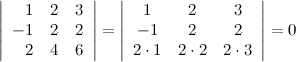
8° Определитель, содержащий нулевую строку, равен нулю.
Пример
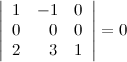
9° Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
Пример
Пусть задан определитель третьего порядка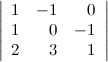 
. Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:
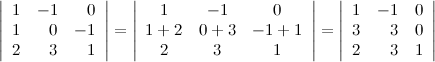
10° Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Пример
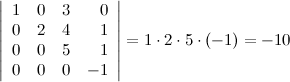
11° Определитель произведения матриц равен произведению определителей: 