Определение
Точка 
, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
1. функция 
определена в точке и ее окрестности;
2. существует конечный предел функции в точке ;
3. это предел равен значению функции в точке , т.е.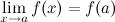 
называется точкой разрыва функции.
Пример
Функция 
не определена в точке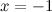 
, а значит, эта точка является точкой разрыва указанной функции.
Определение
Если в точке существуют конечные пределы 
и 
, такие, что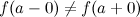 
, то точка называется точкой разрыва первого рода.
Определение
Если хотя б один из пределов или не существует или равен бесконечности, то точка называется точкой разрыва второго рода.
Пример
Задание. Исследовать функцию 
на непрерывность.
Решение. Рассматриваемая функция определена и непрерывна на промежутках 
, 
и 
, на которых она задана непрерывными элементарными функциям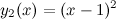и 
, 
и 
соответственно. А тогда, разрыв возможен только на концах указанных промежутков, то есть в точках 
и 
.
Найдем односторонние пределы и значение функции в каждой из точек.
1) Рассмотрим точку . Для нее
Так как 
, то в точке функция терпит разрыв первого рода.
2) Для точки имеем:
Так как односторонние пределы и значение функции в этой точке равны, то это означает, что в точке функция непрерывна.
Ответ. В точке функция терпит разрыв первого рода, а в точке непрерывна.
Пример
Задание. Исследовать функцию 
на непрерывность в точках 
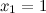и 
.
Решение. 1) Исследуем функцию на непрерывность в точке :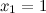
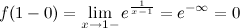
Так как один из односторонних пределов бесконечен, то точка 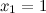- точка разрыва второго рода.
2) Для точки получаем:
и значение функции в точке
Таким образом, в точке заданная функция является непрерывной.
Ответ. 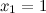- точка разрыва второго рода, а в точке функция непрерывна.
Производные
Производная функции в точке является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости различного рода процессов.
Производная функции равна пределу отношения приращения функции к приращению аргумента, при условии, что последний стремится к нулю:
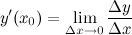
Определение
Функция, которая имеет конечную производную в некоторой точке, называется дифференцируемой в данной точке. Процесс вычисления производной называется дифференцированием функции.
Правила вычисления производных
Пусть функции 
и 
имеют производные в точке 
. Тогда
1. Константу можно выносить за знак производной.
Пример
2. Производная суммы/разности.
Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.
Пример
3. Производная произведения.
Пример
4. Производная частного.
Пример
5. Производная сложной функции.
Производная сложной функции равна производной этой функции по промежуточному аргументу 
, умноженной на производную от промежуточного аргумента по основному аргументу .
и 
и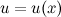меют производные соответственно в точках 
и 
. Тогда
Теорема (О производной обратной функции)
Если функция 
непрерывна и строго монотонна в некоторой окрестности точки и дифференцируема в этой точке, то обратная функция 
имеет производную в точке 
, причем 
.
Дифференциал функции
Пусть функция дифференцируема в точке , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно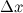 
и нелинейного членов:
где 
при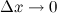 
.
Определение
Дифференциалом функции называется линейная относительно 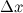часть приращения функции. Она обозначается как 
или 
. Таким образом:
Замечание
Дифференциал функции составляет основную часть ее приращения.
Замечание
Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:
Замечание
Формулу для дифференциала функции можно записать в виде:
Отсюда получаем, что
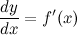
Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.