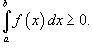1.
Метод непосредственного интегрирования
Приведение к табличному виду или метод непосредственного интегрирования. С помощью тождественных преобразований подынтегральной функции интеграл сводится к интегралу, к которому применимы основные правила интегрирования и возможно использование таблицы основных интегралов.
Пример
Задание. Найти интеграл 
Решение. Воспользуемся свойствами интеграла и приведем данный интеграл к табличному виду.
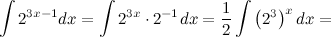
Ответ. 
Внесение под знак дифференциала
В формуле неопределенного интеграла величина 
означает, что берется дифференциал от переменной 
. Можно использовать некоторые свойства дифференциала, чтобы, усложнив выражение под знаком дифференциала, тем самым упростить нахождение самого интеграла. Для этого используется формула
Если нужная функция 
отсутствует, иногда ее можно образовать путем алгебраических преобразований.
Пример
Задание. Внесением под дифференциал найти неопределенный интеграл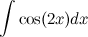 
Решение. Внесем 
под знак дифференциала, тем самым приведя исходный интеграл к табличному.
Ответ. 
В общем виде справедливо равенство:
Пример
Задание. Найти интеграл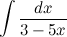 
Решение. Внесем 
под знак дифференциала, тем самым приведя исходный интеграл к табличному.
Ответ.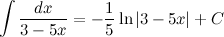 
Интегрирование заменой переменной
Интегрирование заменой переменной или методом подстановки. Пусть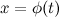 
, где функция 
имеет непрерывную производную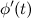 
, а между переменными и 
существует взаимно однозначное соответствие. Тогда справедливо равенство
Определенный интеграл зависит от переменной интегрирования, поэтому если выполнена замена переменных, то обязательно надо вернуться к первоначальной переменной интегрирования.
Пример
Задание. Найти интеграл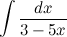
Решение. Заменим знаменатель на переменную и приведем исходный интеграл к табличному виду
Ответ.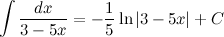
Интегрирование по частям
Интегрированием по частям называют интегрирование по формуле
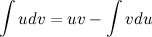
При нахождении функции 
по ее дифференциалу 
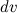можно брать любое значение постоянной интегрирования 
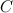, так как она в конечный результат не входит. Поэтому для удобства будем брать 
.
Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой.
Пример
Задание. Найти интеграл 
Решение. В исходном интеграле выделим функции 
и , затем выполним интегрирование по частям.
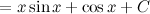
Ответ.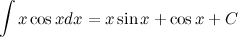 
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЕ»
Пусть функция f (x) непрерывна на замкнутом интервале [ a, b ]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:
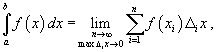
где
Свойства определенного интеграла
Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [ a, b ].
-
где k - константа;
- Если
для всех 
, то 
.
- Если
в интервале [ a, b ], то 