Задачи, аналогичные рассмотренной, характерны для планирования экономической деятельности на любом уровне, от макроэкономческого до внутрипроизводственного. Далеко не для всех этих задач существует возможность эффективного разрешения. Вместе с тем существуют научно обоснованные математические методы, которые позволяют успешно решать многие из этих задач. К числу таких методов относятся методы линейного программирования.
Базовые положения ЛП наглядно иллюстрирует графическая интерпритация. Рссмотрим ее применительно к сформулированной выше двумерной задаче.
Обратимся к системе координат с осью абцисс х1 и осью ординат х2. Построим в этой системе прямую, соответствующую границе плоскости, описываемой первым неравенством в ограничениях задачи. Данная граница задается уравнением
6х1 + 10х2 = 660 (4-15)
Для построения прямой удобно воспользоваться двумя легко вычисляемыми точками, которые могут быть получены путем поочередного приравнивания переменных задачи нулю с последующим вычислением другой координаты. В этих точках прямая пересекает оси координат. Так, при х2 =0, получаем точку пересечения прямой с осью абцисс
x1 = 660/6 = 110 (4-16)
В точке пересечения прямой с осью ординат имеет место х1 = 0, соответственно
х2 = 660/10 =66 (4-17)
Таким образом получаем две точки А и В с координатами (110; 0) и (0; 66) соответственно (рис. 4.1), через которые проходит искомая прямая. Расуждая аналогичным образом, найдем точки пересечения с координатными осями прямой, соответствующей уравнению
0,5х1 +0,3х2 = 47 (4-18)
Данное уравнение задает границу плоскости, описываемой вторым неравенством в ограничениях задачи. Указанные точки пересечения K и L будут иметь координаты (94; 0) и (0; 156,7).
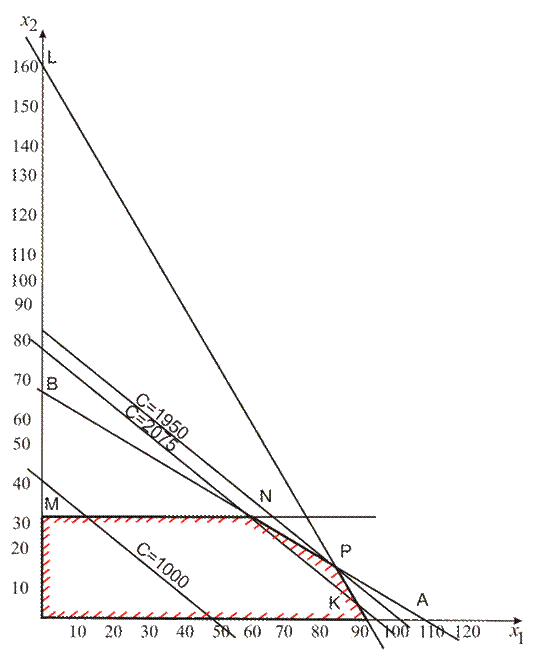
Рисунок 4.1 – Графические построения к задаче ЛП
Прямая, соответствующая границе плоскости, описываемой третьим ограничением, задается уравнением:
1,5х2 = 45 (4-19)
Данная прямая MN будет параллельна оси абцисс и пересекать ось ординат в точке
x2 = 45/1,5 =30 (4-20)
Построенные таким образом прямые АВ, KL и MN будут определять границы области значений переменных х1 , х2 , удовлетворяющих всем трем ограничениям. Поскольку задача содержит еще ограничения на неотрицательность значений переменных
x1 ≥ 0, х2 ≥ 0,(4-21)
указанная область должна быть также ограничена координатными осями.
Выделенная таким образом область пересечения плоскостей, соответствующих всем ограничениям задачи (на рисунке выделена штриховкой), будет характеризоваться тем, что любая точка внутри ее, либо на границе удовлетворяет одновременно всем ограничениям задачи и, таким образом может быть допустимым решением задачи. В этом смысле данную область можно назвать областью допустимых решений (ОДР).
ОДР не дает ответа, какая из ее точек (или какие точки), являются решением задачи. Вместе с тем, она позволяет отыскать данную (данные) точки. Проанализируем с этой целью поведение целевой функции С в пространстве переменных х1, х2. Зададимся каким либо значением для С, например, значением 1950 у.е., которое было вычислено в модельном расчете, рассмотренном выше. Данному варианту плана соответствуют значения переменных х1 = 60 и х2 = 30.
Построим прямую, проходящую через данные точки на осях координат. На рисунке она показана прямой С=1950. Данная прямая характеризуется тем, что координаты всякой точки на ней, будучи подставленные в выражение целевой функции, будут обуславливать значение С= 1950.
Для анализа поведения целевой функции зададим ей любое другое произвольное значение, например 1000 у.е. Тогда будет иметь место уравнение
С = 20х1 +25х2 = 1000 (4-22)
Прямая, соответствующая данному уравнению будет проходить через точки с координатами (50; 0) и (0; 40). По отношению к положению прямой С=1950 она параллельно сместилась по графику вниз, что указывает на снижение значений С в этом направлении. Отсюда следует, что для увеличения эффекта планирования следует перемещать прямую постоянных значений С в противоположном направлении. Однако, такое перемещение возможно только до тех пор, пока прямая пересекает ОДР, так как за пределами ОДР ни одна точка не является допустимой и, следовательно, не может быть принята в качестве решения задачи.
Крайнему допустимому положению указанной прямой будет соответствовать положение касательной к ОДР. Таким образом искомым оптимум задачи будет в точке касания Р. Данная точка лежит на пересечении прямых АВ и KL, что позволяет точно вычислить ее координаты. Для этого достаточно решить систему уравнений:
6х1 +10х2 = 660
(4-23)
0,5х1 +0,3х2 = 47
Решением данной системы являются:
х1 = 85
(4-24)
х2 = 15
Таким образом, оптимальному плану в рассматриваемой задаче соответствует выпуск продукции первого вида в количестве 85 единиц и продукции второго вида в количестве 15 единиц. При этом полностью используется выделенный фонд рабочего времени (660 чел.час.) и наличный запас материала М1 (47 ед.). Материала М2 будет израсходовано 22,5 ед. (1,5х2 = 1.5*15 = 22,5). Доход от реализации выпущенной продукции составит
20*85 +25*15 = 2075 у.е. (4-25)
Как видно, эта сумма превосходит объем реализации 1950 у.е., полученный в рассмотренном ранне модельном расчете. Это максимально возможная величина дохода, которую можно обеспечить при условиях, учитываемых в задаче, т.е. найденный план выпуска продукции является оптимальным.
Полученный план является оптимальным и с точки зрения другого критерия. Если ориентироваться не на доход от реализации, а на максимальную величину выпуска продукции, то получится тот же вариант. Оптимуму соотвествует 85 единиц продукции первого вида и 15 единиц продуции второго вида (суммарный объем выпуска – 100 единиц). Любой другой реализуемый вариант плана приводит к меньшему суммарному объему выпуска продукции.
Приведенный пример показывает, что с помощью графического метода сравнительно легко отыскивается оптимум в задаче линейного программирования. При этом данный оптимум обычно является единственным и находится в одной из вершин ОДР. Однако далеко не всегда задача ЛП имеет единственное решение. Нередки случаи, когда задача имеет более одного решения. Покажем это следующим образом.
Изменим одно из условий рассмотренной задачи. Предположим, что цена, по которой реализуется продукция первого вида составляет не 20 у.е., а 15 у.е. за единицу. Тогда выражение для целевой функции преобразуется к виду:
С= 15х1 + 25х2 (4-26)
В этом случае прямая, соответствующая целевой функции будет иметь на графике другой наклон, в результате чего предельное ее положение совпадет на ОДР с гранью PN. Отсюда следует, что всякая точка на данной грани ОДР будет являться равноценным и оптимальным решением задачи. К примеру, точке N, где х1 = 60; х2 = 30, будет иметь место
С = 15*60+25*30 = 900 + 750 = 1650 у.е. (4-27)
Такое же значение С будет в точке N (15*85+25*15=1275+375=1650), равно, как и во всех промежуточных точках на грани PN, число которых бесконечно. Чтобы решить вопрос о том, какую из этих точек закрепить в принимаемом плане, можно ввести дополнительное условие. Если, например, желательно довести до максимума не только доход от реализации продукции, но и суммарный объем выпуска продукции, то в качестве решения следует принять х1 = 85, х2 = 15, которому соответствует объем выпуска 100 единиц. Если же задаться целью обеспечить максимальный выпуск продукции второго вида, следует остановиться на варианте х1 = 60, х2 = 30. В этом случае максимум дохода при новых условиях планировании и, одновременно, максимально возможный выпуск продукции второго вида. Отсюда видно, что методы линейного программирования позволяют всесторонне оценивать различные варианты планирования и уверенно выбирать наилучший из них в конкретных условиях.