Контрольная работа
по дисциплине «Специальные разделы высшей математики»
Вариант 3
Выполнила:
ст.гр. ПГСм-67б Федоренко В.Р.
Руководитель:
к.т.н. доцент Симогин А.А.
Макеевка 2017
Тема 1. Статистическая обработка экспериментальных данных. Оценка параметров.
Задание1.
По данной выборке случайной величины X вычислить все основные эмпирические характеристики: математическое ожидание mx *, дисперсию D *, несмещённую дисперсию S 2, среднее квадратическое отклонение σ x *, построить доверительный интервалдля математического ожидания, построить доверительный интервал для дисперсии (доверительную вероятность положить равной 0,95).
5,8 2,8 4,6 3,2 3,0 2,5 4,4 3,5 4,9 2,9 5,1 4,3 3,7 3,5 3,6
7,3 5,1 6,3 8,1 3,5 2,7 2,6 2,4 6,4 4,4 5,0 5,1 3,7 6,9 4,8
3,2 8,0 3,6 7,4 4,9 5,1 3,7 2,5 3,0 2,3 3,9 3,2 9,2 7,4 5,1
4,5 2,8 2,7 5,0 5,9 6,8 5,0 9,0 8,3 6,8 5,1 4,3 9,4 4,1 5,2
Решение
Наибольший элемент выборки равен 9,4, наименьший – 2,3, размах выборки равен7,1. Учитывая, что элементы выборки распределены не равномерно на этом интервале, ширину первых шести частичных интервалов выберем равной 1,01, апоследнего интервала – 1,04. Составим интервальный вариационный ряд, подсчитав числоэлементов выборки, попавших в каждый частичный интервал. Если значение элементасовпадает с левой границей частичного интервала, то его следует относить к данномуинтервалу. Значение, совпадающее с правой границей, не включается в данный интервал. Впоследний интервал включается и то значение, которое совпадает с его правойграницей. Вычисления проводятся в таблице, содержащей вариационный ряд и строки, необходимые для вычисления начальных моментов.
По результатам вычислений, получим:
| i | 
| 
| 
| 
| 
| 
| 
|
| 2.3-3.31 | 2.786667 | 41.8 | 116.4827 | 324.5984 | 904.5474 | ||
| 3.31-4.32 | 3.783333 | 45.4 | 171.7633 | 649.8379 | 2458.554 | ||
| 4.32-5.33 | 4.9 | 83.3 | 408.17 | 2000.033 | 9800.162 | ||
| 5.33-6.34 | |||||||
| 6.34-7.35 | 6.8 | 231.2 | 1572.16 | 10690.69 | |||
| 7.35-8.36 | |||||||
| 8.36-9.4 | 9.2 | 27.6 | 253.92 | 2336.064 | 21491.79 | ||
| ∑ | 290.1 | 1609.536 | 10090.69 | 69713.74 |
Определяем несмещённую оценку S2 неизвестной дисперсии:
Измерение X является случайной величиной с неизвестным математическим ожиданием 
, и известным средним квадратическим отклонением 
. Суммируя все измерения и деля полученную сумму на число измерений n=60, найдём оценку : =289,5/60=4,825. Решим уравнение Ф(εγ)=γ/2 при γ=0,95: Ф(εγ)=0,95/2=0,475. По значению функции Лапласа, равному 0,475, по таблице определяем соответствующее значение аргумента этой функции: εγ=1,96.
С вероятностью 0,95, для доверительного интервала математического ожидания, справедливо выражение:
Вычисляя, получим доверительный интервал: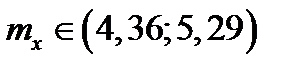 
с вероятностью γ=0,95.
Доверительный интервал для дисперсии, с вероятностью γ=0,95, будет иметь следующий вид:
При большом объеме выборки граничные значения распределения 
и 
определяем по формулам:
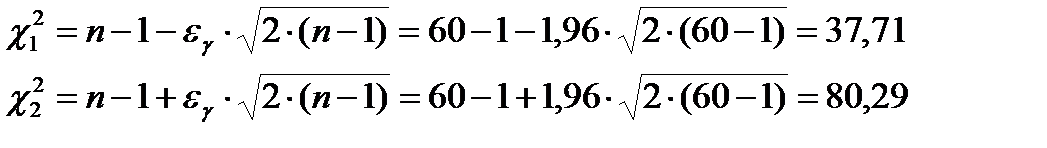
Вычисляя, получим доверительный интервал: 
с вероятностью γ=0,95.
Задание2.
Для оценки вероятности появления дефектных деталей, выпускаемыхнекоторой производственной линией, было обследовано n деталей. Среди обследованных деталей было обнаружено k дефектных деталей. Построить доверительный интервалдля истинной вероятности появления дефектной детали с доверительной вероятностью,равной 0,95. Решить задачу при n = 100 и k = 19.
Решение
Запишем доверительный интервал для вероятности события:
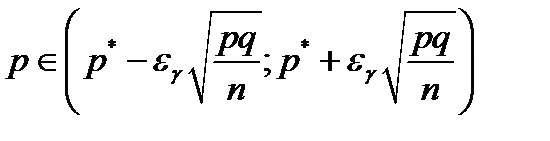с вероятностью γ. В данном случае p * = 19/100 ≈ 0,19. По таблицам нормального распределения по заданной доверительной вероятности
γ = 0,95 находим: εγ= 1,96. Найдём доверительный интервал двумя способами.
Первый способ. Вместо неизвестной вероятности появления дефектной детали
подставим её оценку: 
.
Вычисляя, получим: 
. Или 
с вероятностью, приближённо равной 0,95.
Второй способ. Вместо неизвестного произведения pq подставим его наибольшее
значение (при 0 ≤ p ≤ 1), равное 0,25: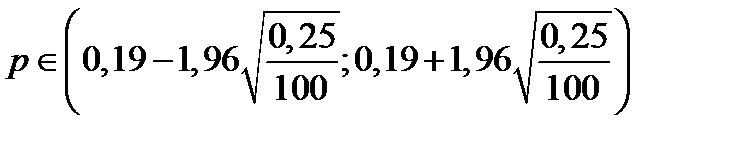 
. Вычисляя, получим 
. Или 
с вероятностью не меньшей чем 0,95. Второй способ надёжнее, хотя он даёт более широкий интервал.
Вычислим точные значения границ доверительного интервала. Для этого найдём корни уравнения по формулам:
Следовательно p∈(0,125; 0,277) с вероятностью, равной 0,95.
Тема 2. Проверка статистических гипотез
Задание3.
По представленной в задании 16 выборке построить полигон и гистограмму. Подобрать подходящий теоретический закон распределения вероятностей и проверить гипотезу о соответствии эмпирического закона распределения выбранному теоретическому при уровне значимости α = 0,05.
Решение
По данным задания 1 составим следующую таблицу:
| i | ∑ | |||||||
| zi–1÷zi | 2.3-3.31 | 3.31-4.32 | 4.32-5.33 | 5.33-6.34 | 6.34-7.35 | 7.35-8.36 | 8.36-9.4 | |
| Δi | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.04 | |
| 2.79 | 3.78 | 4.9 | 6.8 | 9.2 | |||
| ni | ||||||||
| pi* | 0.25 | 0.2 | 0.28 | 0.05 | 0.083 | 0.083 | 0.05 | |
| pi*/Δi | 0.25 | 0.198 | 0.28 | 0.05 | 0.082 | 0.082 | 0.048 |
В таблице используются следующие обозначения: Δi – ширина i–го интервала; pi* –эмпирическая вероятность попадания в i-й интервал. В последней строке представлены значения эмпирической плотности распределения вероятностей для частичных интервалов. По данным этой строки строим гистограмму и полигон распределения, которые в данном случае являются двумя различными графическими представлениями эмпирической плотности распределения вероятностей изучаемой величины (рис. 7.1).
Рис.1– Гистограмма и полигон распределения, построенные по интервальному вариационному ряду
Из графиков видно, что эмпирическое распределение очень похоже на теоретическое экспоненциальное распределение. В пользу выбора экспоненциального распределения в качестве гипотетического говорит и тот факт, что оценки математического ожидания и среднего квадратического отклонения достаточно близки. Известно, что в случае экспоненциального распределения эти параметры равны.
Для оценки параметра λ экспоненциального распределения F(x) = 1− e−λx, f (x) = λe−λx, x ≥ 0, λ > 0, используем соотношение mx = 1/λ, заменив математическое ожидание mx его оценкой mx*, вычисленной в примере 6.4: λ* = 1/mx* = 1/4,834= 0,207 ≈ 0,2.
Таким образом, гипотетическое распределение имеет вид:
F(x) = 1− e−0,2x,f (x) = 0,2⋅ e−0,2x, x ≥ 0.
Теоретические вероятности попадания случайной величины в частичные интервалы вычисляются по формуле: pi = F(zi) – F(zi–1), i = 1, 2, …, 8. Например, p1 = F(0,2) – F(0) = (1− e−0,2⋅3,31) − (1− e−0,2⋅2,3) = 1− 0,641 = 0,359. Тогда np1 = 60 ⋅ 0,359 = 21,54. Выполняя аналогичные вычисления для всех интервалов, внесём полученные результаты в таблицу. Правая граница последнего интервала принята равной ∞, так как в случае гипотетического распределения случайная величина может принимать значения в интервале (0; ∞).
В соответствии с теорией значения npi не должны быть меньше пяти.
Определение параметра χ2
| i | zi–1÷zi | ni | F(zi) | F(zi–1) | pi | npi | ni–npi | (ni–npi)2/(npi) |
| 2.3-3.31 | 0.484 | 0.000 | 0.484 | 29.051 | -14.051 | 6.796 | ||
| 3.31-4.32 | 0.579 | 0.484 | 0.094 | 5.661 | 6.339 | 7.099 | ||
| 4.32-5.33 | 0.656 | 0.579 | 0.077 | 4.625 | 12.375 | 33.107 | ||
| 5.33-6.34 | 0.719 | 0.656 | 0.063 | 3.779 | -0.779 | 0.161 | ||
| 6.34-7.35 | 0.770 | 0.719 | 0.051 | 3.088 | 1.912 | 1.184 | ||
| 7.35-8.36 | 0.812 | 0.770 | 0.042 | 2.523 | 2.477 | 2.431 | ||
| 8.36-9.4 | 1.000 | 0.812 | 0.188 | 11.272 | -8.272 | 6.071 | ||
| Σ | 1.000 | 56.848 |
Полученное значение равноχ2 =56,848.
Так как окончательный расчёт величины χ2 проводился по 7-ти интервалам и один параметр был оценён (λ) по этой же выборке, то число степеней свободы распределения χ2 будет равно k=7–2=5. По таблицам распределения χ2 с 5 степенями свободы и с уровнем значимости α = 0,05 находим критическое значение χα2=11,07. Вычисленное значение χ2 больше критического. Следовательно, гипотеза о соответствии эмпирического и теоретического распределения отвергается. Это значит, что нельзя рассматривать исследуемую величину как величину, распределённую по экспоненциальному закону с параметромλ=0,2.
Задание 4.
Используя данные таблицы задания 16, с помощью критерия квантилей проверить гипотезу о том, что медиана распределения равна эмпирическому математическому ожиданию.
5,8 2,8 4,6 3,2 3,0 2,5 4,4 3,5 4,9 2,9 5,1 4,3 3,7 3,5 3,6
7,3 5,1 6,3 8,1 3,5 2,7 2,6 2,4 6,4 4,4 5,0 5,1 3,7 6,9 4,8
3,2 8,0 3,6 7,4 4,9 5,1 3,7 2,5 3,0 2,3 3,9 3,2 9,2 7,4 5,1
4,5 2,8 2,7 5,0 5,9 6,8 5,0 9,0 8,3 6,8 5,1 4,3 9,4 4,1 5,2
Решение
Суммируя все элементы выборки и поделив полученную сумму на число измерений n=60, найдём оценку математического ожидания : =289,5/60=4,825. Найдем число элементов, которое меньше математического ожидания: k=31. Для медианы р=0,5. Следовательно:
При уровне значимости α=0,05, решим уравнение Ф(tα)=(1 –0,05)/2=0,475. По таблицам находим: tα=1,96. Так как |t | < tα, то гипотезу о равенстве медианы распределения, эмпирическому математическому ожиданию можно принять.
Задание 5.
Предположим, что две первые строки таблицы задания 16 являются измерениями случайной величины X, а две последние – измерениями случайной величины Y. Проверить гипотезу о равенстве математических ожиданий величин X и Y.
X: 5,8 2,8 4,6 3,2 3,0 2,5 4,4 3,5 4,9 2,9 5,1 4,3 3,7 3,5 3,6
7,3 5,1 6,3 8,1 3,5 2,7 2,6 2,4 6,4 4,4 5,0 5,1 3,7 6,9 4,8
Y: 3,2 8,0 3,6 7,4 4,9 5,1 3,7 2,5 3,0 2,3 3,9 3,2 9,2 7,4 5,1
4,5 2,8 2,7 5,0 5,9 6,8 5,0 9,0 8,3 6,8 5,1 4,3 9,4 4,1 5,2
Решение
Рассмотрим две выборки. Первая выборка Xn=(x1,x2, …,xn) представляет измерения случайной величины X, вторая выборка Yk=(y1,y2,…, yk) представляет измерения случайной величины Y. Пусть вычислены математические ожидания:
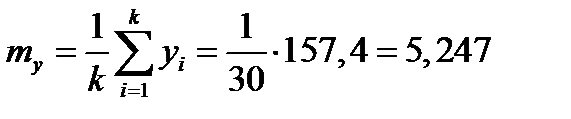
Проверяем гипотезу о том, что математические ожидания этих величин одинаковы. Выдвигаем гипотезу H0: mx=my, т.е. математические ожидания одинаковы. Альтернативной гипотезой будет H1: mx ≠ my.
Вычислим оценки дисперсии по первой и второй выборкам Sx2 и Sy2:
Вычислим S: 
Далее вычислим t: 
Решим уравнение P{|t |≥ tα} = 0,05. По таблицам распределения Стьюдента с числом степеней свободы 58 находим tα = 2. Так как | t| =-0,125< tα= 2, то гипотезу о равенстве математических ожиданий, можно принять.