ПРОБЛЕМА СКРЫТЫХ ПАРАМЕТРОВ В КВАНТОВОЙ МЕХАНИКЕ
Ю.П. Рыбаков
Российский университет дружбы народов,
Кафедра теоретической физики
E-mail: soliton4@mail.ru
Аннотация
Обсуждаются некоторые принципиальные вопросы квантовой механики, связанные с попытками введения скрытых параметров, позволяющих дать описание индивидуальных квантовых событий. Прослеживается история вопроса: от теоремы фон Неймана и парадокса Эйнштейна – Подольского – Розена (ЭПР) до неравенств Белла. Строится стохастическое представление квантовой механики, в котором образом частицы является солитонное решение фундаментальных нелинейных уравнений поля, а волновая функция выступает как сумма комплексных солитонных конфигураций, относящихся к статистически независимым реализациям индивидуальных событий и играющих роль нелокальных скрытых параметров. В таком стохастическом представлении квантовое правило вычисления средних как эрмитовых квадратичных форм является следствием заложенной в волновой функции симплектической структуры, а уравнение Шредингера прямо вытекает из уравнений движения фундаментального поля. Показывается, что связь спина со статистикой является следствием протяженности частиц. В качестве примера рассматривается нелинейная спинорная модель типа Гейзенберга – Иваненко, в которой существуют солитонные решения, описывающие частицы со спином ½. На базе этих решений строится синглетная конфигурация из двух частиц, в стохастическом представлении вычисляется спиновый ЭПР-коррелятор и показывается, что он совпадает с квантовым.
- СОЗДАНИЕ КВАНТОВОЙ МЕХАНИКИ
Квантовая механика возникла как обобщение классической механики, оптики и электродинамики в связи с необходимостью объяснения ряда экспериментальных фактов, относящихся к явлениям, происходящим на малых расстояниях порядка размера атомов. Прежде всего, это оптические спектры, объяснить которые никак не удавалось. В частности, И. Бальмер (1885) и позднее И. Ридберг (1890) нашли формулу для наблюдаемых частот водородного спектра:
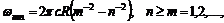(1.1)
где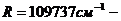 
постоянная Ридберга, c – скорость света. Был обнаружен и комбинационный принцип В. Ритца (1908), согласно которому наблюдаемые частоты связаны между собой соотношением
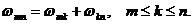(1.2)
После открытия Дж.Дж. Томсоном электрона (1897) Х. Нагаока (1903) предложил планетарную модель атома, подтвержденную в опытах Э. Резерфорда (1910). Согласно этой модели, электроны в атоме движутся вокруг компактного положительно заряженного ядра, и поэтому в соответствии с законами классической электродинамики, они должны излучать и, в конце концов, теряя энергию, падать на ядро. Таким образом, классический атом Нагаоки – Резерфорда оказывается неустойчивым и не может существовать.
Все указанные факты настойчиво говорили о необходимости изменения классических представлений. Первую попытку в этом направлении предпринял М. Планк (1900), который, изучая термодинамику излучения абсолютно черного тела, пришел к формуле для средней энергии, приходящейся на одну моду с частотой ω:
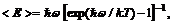(1.3)
где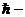 
постоянная Планка, k – постоянная Больцмана, T – абсолютная температура тела. По совету Больцмана, Планк преобразовал выражение (1.3), приведя его к виду
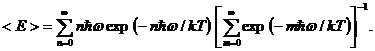(1.4)
Проанализировав формулу (1.4), Планк пришел к выводу о том, что она представляет собой среднее по Больцману от энергии колебаний одной моды, которая по какой-то неизвестной причине может принимать лишь дискретные значения
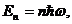(1.5)
кратные элементарному кванту энергии
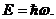(1.6)
В результате, в значительной мере под влиянием Больцмана, Планк пришел к выводу о том, что атомы вещества могут излучать энергию только порциями, характерными для каждой частоты и равными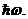 
Впоследствии А. Эйнштейн (1905), анализируя установленные А. Столетовым (1890) законы фотоэффекта, которые также не укладывались в классическую схему, принял под влиянием работ Планка гипотезу о существовании квантов света – фотонов, энергия которых задается формулой (1.6). Таким образом, выяснилось, что электромагнитная энергия не только испускается, но и поглощается, а значит, и распространяется порциями.
Так, фотоны стали реальностью. Импульс фотона p можно найти из закона сохранения энергии и импульса. В самом деле, скорость v фотона совпадает со скоростью света c, и поэтому из теоремы живых сил выводим dE = (v d p) = (c d p) = d (сp) = d(pc), откуда E = pc,
или, согласно (1.6),
p =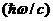 
s =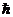 
k, (1.7)
где s - единичный вектор вдоль направления движения фотона, а k – волновой вектор. Формулы Планка – Эйнштейна (1.6) и (1.7) отражают фундаментальное свойство света –
корпускулярно-волновой дуализм, поскольку их левые части, т. е. энергия и импульс фотонов, выражают свойства частиц, а их правые части, т. е. частота и волновой вектор, выражают свойства света как поля. Именно эти соотношения, получившие прямое подтверждение в опытах А. Комптона (1923) по рассеянию фотонов на электронах, и послужили основой для введения новых квантовых представлений сначала Н. Бором (1913), а затем Луи де Бройлем (1923).
Бор заметил, что с учетом закона сохранения энергии можно переписать формулы (1.1) и (1.2) в более привычном виде, если ввести понятие терма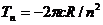 
и отождествить 
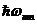с энергией излученного фотона, а величину 
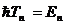с энергией электрона в атоме. В таком случае получается знаменитое соотношение частот Бора:
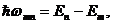(1.8)
из которого вытекает существование дискретного набора энергетических уровней электрона в атоме:
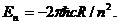(1.9)
Однако главной заслугой Бора было то, что ему удалось в результате некоторых рассуждений раскрыть смысл постоянной Ридберга R, выразив ее через известные фундаментальные постоянные. Этот результат был получен на основании сформулированного Бором принципа соответствия, согласно которому при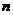 
>> 1, когда электрон находится вдали от ядра, должны соблюдаться законы классической физики. В частности, минимальная частота излучения должна совпадать с частотой ω обращения электрона вокруг ядра. Таким образом, для 
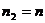>> 1,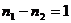 
из (1.8) и (1.9) выводим соотношение
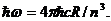(1.10)
С другой стороны, для круговой орбиты радиуса r можно записать условие равновесия
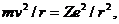(1.11)
где Ze – заряд ядра. Вспоминая, что для кругового движения ω = v/r, из (1.10) и (1.11)
можно выразить скорость электрона v и радиус орбиты r как функции от главного квантового числа n. Кроме того, можно вычислить полную энергию электрона в атоме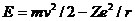 
и момент импульса L = mvr. Сравнение энергии с (1.9) и позволило Бору получить известную формулу для постоянной Ридберга в спектрах водородоподобных атомов:
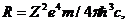(1.12)
а также вывести из нее знаменитое правило квантования:
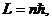(1.13)
которое означает, что на допустимых орбитах момент импульса электрона кратен постоянной Планка. Таким образом, Бор обобщил условие (1.13) на любые целые значения n, хотя и пользовался принципом соответствия, верным лишь для n >> 1.
Чтобы понять физический смысл условия (1.13), де Бройль (1923) делает допущение о том, что электрон является источником некоторых колебаний, которые распространяются в виде волны вдоль орбиты электрона, и при этом длина волны n раз укладывается вдоль его траектории. Руководствуясь оптико-механической аналогией Гамильтона, де Бройль связывает частоту ω и волновой вектор k волны с энергией E и импульсом p электрона теми же соотношениями (1.6) и (1.7), что и для фотона. Тем самым предполагается универсальность соотношений Планка – Эйнштейна, т. е. их справедливость для любых частиц. Однако, приняв существование такой особой волны, де Бройль заметил, что ее фазовая скорость
u = ω/ k = E/p (1.14)
не совпадает со скоростью электрона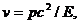 
и поэтому согласованность движений
электрона с распространением волны оказывается проблематичной. Чтобы разрешить указанное противоречие, де Бройль сопоставил с электроном не отдельную плоскую волну, а пакет волн (с разными k). Тогда, если учесть релятивистское соотношение
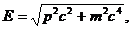
нетрудно убедиться в том, что групповая скорость пакета в точности совпадает со скоростью электрона:
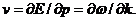
Все эти соображения были изложены де Бройлем в его диссертации (1924), которую он послал Эйнштейну [1]. Эйнштейн откликнулся восторженной статьей, в которой пропагандировал идеи де Бройля и предлагал искать проявления волновых свойств электронов в молекулярных пучках. Такие эксперименты действительно были поставлены, но гораздо позже, первая же реакция в физическом сообществе на выдвинутую де Бройлем гипотезу была очень сдержанной. Так, Э. Шредингер очень критично отнесся к работам де Бройля и только после настоятельных просьб П. Дебая приступил к поискам возможных уравнений, которым мог бы удовлетворять волновой пакет, связанный, по мысли де Бройля, с электроном.
В качестве первого шага Шредингер рассмотрел стационарный волновой пакет некоторого комплексного поля ψ, который мог бы быть сопоставлен с электроном, движущимся в потенциальном поле V (r). Если учесть нерелятивистский закон сохранения энергии
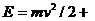V (r) (1.15)
и соотношение (1.6), то такой пакет должен иметь вид
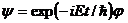(r). (1.16)
С другой стороны, согласно (1.7) и (1.15), пакет (1.16) должен соответствовать набору волновых векторов, удовлетворяющих условию вида
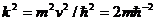[ E - V (r)]. (1.17)
Поэтому функция φ (r), как и всякая волновая амплитуда, должна быть решением уравнения Гельмгольца
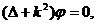
откуда, согласно (1.16) и (1.17), сразу следует стационарное уравнение Шредингера:
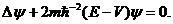(1.18)
Кстати, энергию E можно исключить из (1.18), если учесть соотношение (1.16) и положить
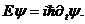
В результате (1.18) примет привычный вид нестационарного уравнения Шредингера [2]:
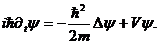(1.19)
Опираясь на уравнение (1.19), Шредингер объяснил опыты К. Дэвиссона и Л. Джермера (1927) по рассеянию электронов на монокристаллах никеля, в которых были получены типичные дифракционные пики. Аналогичные опыты, но по рассеянию электронов на поликристаллических пленках, также подтвердившие волновые свойства электронов, были выполнены Дж.П. Томсоном (1927), П.С. Тартаковским (1928) и многими другими физиками.
Однако главной целью Шредингера было применение уравнения (1.19) для объяснения оптических спектров. В частности, если рассмотреть кулоновский потенциал взаимодействия электрона с ядром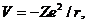 
то оказалось, что все квадратично-интегрируемые решения уравнения (1.18) в точности соответствуют дискретным уровням энергии электрона 
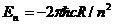в водородоподобном атоме [2]. Получив столь убедительное подтверждение справедливости своего уравнения, Шредингер попытался выяснить физический смысл введенной им волновой функции ψ. Первой его мыслью было отождествить величину
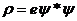, (1.20)
где e – заряд электрона, с плотностью электрического заряда в атоме. В самом деле, из уравнения (1.19) нетрудно вывести уравнение непрерывности
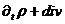j = 0, (1.21)
выражающее закон сохранения электрического заряда. При этом плотность электрического тока имеет вид
j =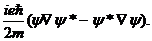 
Чтобы подтвердить свою догадку, Шредингер рассмотрел задачу о возбуждении атома падающей на него электромагнитной волной. Ясно, что возбужденный атом будет излучать, и мощность излучения будет определяться изменением дипольного момента атома, как это следует из законов электродинамики. Согласно (1.20), дипольный момент атома имеет вид
P =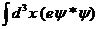 
r. (1.22)
Представив решение уравнения (1.19) в виде разложения по собственным функциям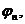 
отвечающим стационарным состояниям (1.16) с энергиями 
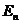, т. е. положив
(r), (1.23)
из (1.22) и (1.23) нетрудно вывести структуру дипольного момента атома:
P =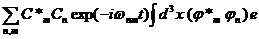 
r. (1.24)
Как видно из (1.24), дипольный момент атома содержит набор слагаемых, пульсирующих с частотами переходов (1.8). Как следует из электродинамики, мощность излучения пропорциональна квадрату второй производной по времени от дипольного момента и поэтому определяется величинами вида
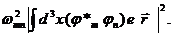(1.25)
Как выяснилось, именно величины типа (1.25) рассматривал в своих работах
В. Гейзенберг (1925), пытаясь объяснить интенсивность спектральных линий в рамках развитой им матричной механики. Таким образом, искусственная схема Гейзенберга получала естественное обоснование в рамках теории Шредингера.
Однако интерпретация величины (1.20) как плотности заряда была подвергнута пересмотру М. Борном (1926). Основной аргумент Борна сводился к тому, что волновыми свойствами, согласно де Бройлю, обладают любые материальные частицы, в том числе и нейтральные атомы и молекулы, что в самом деле было вскоре подтверждено. Поэтому логично считать, что величина
w (t, r) = ψ*ψ (t, r) (1.26)
связана с плотностью вероятности обнаружить микрочастицу в точке r. Таким образом, согласно (1.26), волновая функция ψ выступает как амплитуда вероятности соответствующего процесса, а элементарная вероятность встретить частицу в области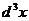 
с центром r оказывается равной
dW = w (t, r) 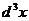= ψ*ψ (t, r) 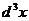. (1.27)
Проиллюстрируем статистический подход Борна, рассмотрев задачу о прохождении электронов сквозь систему N щелей в непроницаемом плоском экране (решетку). Пусть электроны инжектируются точечным источником S вдали от экрана и по прохождении решетки регистрируются детектором в некоторой области dx с центром x. Тогда вероятность dW = w(x) dx попасть в эту область отдельному электрону складывается из вероятностей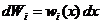 
попасть туда, пройдя сквозь щель с номером i, т. е.
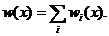(1.28)
Однако, проходя отдельную щель, электрон «чувствует» и другие щели. Поэтому должно быть справедливо разложение
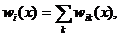(1.29)
где слагаемые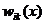 
следует рассматривать как функции «влияния» щелей с номерами i и k. Нетрудно видеть, что для классических частиц такое влияние различных щелей должно отсутствовать. Объединяя соотношения (1.27), (1.28) и (1.29), найдем
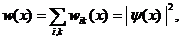(1.30)
откуда вытекает соотношение
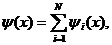(1.31)
выражающее принцип суперпозиции П.А.М. Дирака. Согласно этому принципу, амплитуда вероятности некоторого события, реализуемого по нескольким каналам, складывается из амплитуд вероятностей отдельных каналов.
Из (1.30) и (1.31) нетрудно вывести структуру функции влияния отдельных каналов:
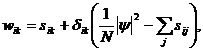(1.32)
где использована вспомогательная вещественная величина
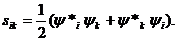
В частности, из (1.32) вытекает, что каждый отдельный электрон проходит сквозь какую-то одну щель, «чувствуя» при этом и другие щели.
- ОСНОВЫКВАНТОВОЙ ТЕОРИИ ИЗМЕРЕНИЙ
Основные положения квантовой теории измерений были выдвинуты П. Иорданом и П.А.М. Дираком (1926) исходя из представления о волновой функции как векторе абстрактного гильбертова пространства Ħ, т. е. полного нормированного пространства со
скалярным произведением, для которого Дирак предложил очень удобное скобочное обозначение:
< α | β > = < β | α >*, (2.1)
где | α > - произвольный вектор из Ħ, а < α | - ему сопряженный.
С точки зрения элементарной практики измерений, следует различать понятия наблюдения, измерения и приготовления состояний системы. Под наблюдением обычно понимают одиночное испытание, т. е. индивидуальный наблюдательный акт, выполняемый с некоторой индивидуальной ошибкой δ a, или погрешностью наблюдения некоторой величины a, определяемой точностью используемых приборов. Под измерением же понимают серию наблюдений, выполненных в одних и тех же условиях. При этом статистическая ошибка измерения Δ a находится как среднеквадратичное отклонение:
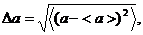(2.2)
где <> - знак усреднения по серии наблюдений (обычно это взятие среднего арифметического). Наконец, приготовление состояния системы – это создание условий, при выполнении которых ряд признаков исследуемой системы воспроизводится при наблюдениях с максимально допустимой точностью (фиксируется).
Пусть для измеряемых величин A, B, C,… в одиночных испытаниях получаются некоторые их значения (для простоты дискретные):
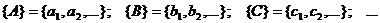
Если в условиях опыта величина A принимает некоторое фиксированное значение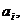 
тогда как величина B измеряется, то вероятность 
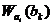встретить значение 
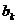подчиняется условию нормировки
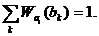(2.3)
Допустим теперь, что подобные измерения выполнены для различных значений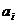 
и выбраны испытания с одним исходом 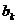. Если рассматривать это как новую серию измерений, то условие нормировки для нее должно быть аналогичным (2.3), т. е.
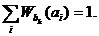(2.4)
Однако, по существу, мы воспользовались результатами измерений из различных серий, и поэтому могли бы написать условие нормировки вида
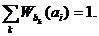(2.5)
Чтобы примирить указанные точки зрения, Дирак принял условие симметрии
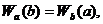(2.6)
получившее известность как принцип микро-обратимости. Аналогичное соотношение (но уже для плотностей вероятности) должно выполняться и в случае непрерывного спектра значений измеряемых величин. Объединяя его с принципом Борна (1.30), замечаем, что в общем случае волновая функция системы определяется двумя наборами величин – измеряемых и фиксируемых:
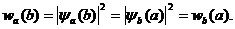(2.7)
Принимая во внимание свойство (2.1) скалярного произведения и тот факт, что вектор в гильбертовом пространстве задан с точностью до фазового множителя, из (2.7) выводим
общую структуру волновой функции квантовой системы:
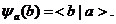(2.8)
Индекс a в (2.8) характеризует фиксированные величины и носит название индекса состояния, а индекс b относится к измеряемым величинам и носит название индекса представления. Таким образом, согласно (2.8), волновая функция представляется как скалярное произведение двух различных базисных векторов в Ħ. В частности, если воспользоваться произвольным ортонормированным базисом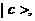 
то с учетом условия полноты
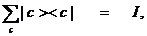
где I – единичный оператор, из (2.8) получаем известный закон преобразования волновой функции при переходе к новому базису (новому представлению):
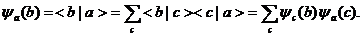(2.9)
Зафиксируем теперь величину b и будем измерять некоторую величину A. Тогда среднее значение нашей наблюдаемой величины будет следующим:
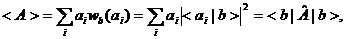(2.10)
где введен самосопряженный оператор
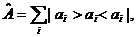(2.11)
отвечающий наблюдаемой A. Формула (2.11) соответствует так называемому диагональному представлению наблюдаемой A, в котором базисными векторами выступают собственные векторы оператора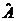 
с собственными значениями 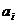. Переход к любому другому представлению осуществляется с помощью преобразования базиса (2.9). Формула (2.10) задает квантовое правило вычисления средних как эрмитовых квадратичных форм, порождаемых самосопряженными операторами.
Как важное следствие формулы (2.11) получаем известное правило о совместной измеримости двух наблюдаемых A и B, т. е. о существовании общего собственного вектора у соответствующих операторов. Как известно, для этого необходимо и достаточно, чтобы эти операторы коммутировали.
Для описания простейших наблюдаемых рассмотрим одномерный случай, когда уравнение Шредингера принимает вид
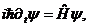(2.12)
где введен оператор Гамильтона
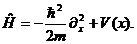(2.13)
Пусть ψ (t,x) – нормированный волновой пакет, центр которого определим соотношением
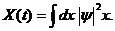(2.14)
Дифференцируя уравнение (2.14) по времени с учетом (2.12), найдем
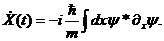(2.15)
Соотношение (2.15), известное как первое уравнение Эренфеста, выражает среднюю скорость частицы через ее средний импульс. В связи с этим оператор импульса должен иметь вид
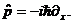(2.16)
Найденное представление, в котором оператор координаты частицы совпадает с x, называется координатным, или конфигурационным. С помощью (2.16) несложно оценить дисперсию координаты Δx или импульса Δp:
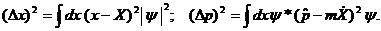(2.17)
С другой стороны, используем условие нормировки пакета:
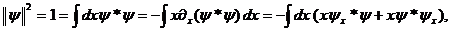
в котором оценим правую часть с помощью неравенства Шварца
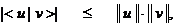(2.18)
где взято u = xψ, v =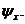 
Принимая для простоты, что центр пакета помещен в начало координат, т. е. X = 0, из (2.17) и (2.18) выводим неравенство
1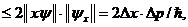 
(2.19)
известное как соотношение неопределенностей Гейзенберга.
Выяснение смысла соотношения (2.19) играет ключевую роль в построении той или иной интерпретации квантовой механики и, в первую очередь, интерпретации самой волновой функции. Известны две физически различные интерпретации, которые обычно связывают с именами Эйнштейна и Бора:
- Статистическая интерпретация (Эйнштейн) принимает, что волновая функция дает вероятностное описание ансамбля тождественных микросистем, так называемого квантового статистического ансамбля.
- Копенгагенская интерпретация (Бор) принимает, что волновая функция дает вероятностное описание индивидуальной микросистемы.
Если первая точка зрения подчеркивает, что выводы квантовой механики нельзя относить к индивидуальной микросистеме (к отдельному электрону или фотону), поскольку они носят статистический характер, то вторая точка зрения предполагает, что волновая функция дает максимально полное описание индивидуального микропроцесса и такое описание не может быть детерминированным. Следует подчеркнуть, что на опыте обе указанные позиции неразличимы, так как вероятностные предсказания могут быть проверены только в результате статистической обработки серии наблюдений.
Проиллюстрируем различие этих точек зрения на примере известного опыта по дифракции электронов, который выполнили в 1949 году Л. Биберман, Н. Сушкин и
В. Фабрикант [3]. Они использовали чрезвычайно слабый ток, пропуская электроны через кристаллический образец по одному и регистрируя их попадание на экран в отдельные точки. Выяснилось, что с течением времени, по мере накопления электронов, на экране вырисовывалась типичная дифракционная картина. Аналогичные опыты были выполнены и с одиночными фотонами Дж. Тейлором (1908), С.И. Вавиловым (1934),
Л. Яноши (1957) и др. [4].
Результаты этих опытов подтверждают гипотезу де Бройля о том, что некоторое волновое поле сопровождает каждый отдельный электрон (или фотон), однако оно обнаруживается лишь статистически. Тем самым выявляется статистическая природа корпускулярно-волнового дуализма: волна, сопровождающая частицу, проявляется только в серии испытаний, а не в отдельном наблюдении. Таким образом, электрон, как и любая другая микрочастица, не может считаться ни обычной классической частицей, ни волной, - это нечто третье. Его нельзя считать классической частицей, так как при прохождении через образец он особым, резонансным образом взаимодействует сразу со многими сотнями атомов – в противном случае в серии испытаний не могла бы формироваться дифракционная картина. Его нельзя считать и волной, так как на экране он попадает в какое-то определенное место, локализуется.
Чтобы понять поведение электрона в рамках двух вышеуказанных интерпретаций, рассмотрим самый простой опыт – дифракцию электрона с импульсом p на прямолинейной щели шириной d, вырезанной в непроницаемом экране.
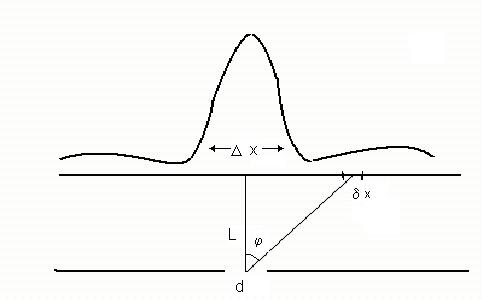
Рис. 1
Пусть экран регистрации расположен на расстоянии L от щели (рис. 1), а электрон,
прошедший посередине щели, отклонился на угол φ, попав на экран в область, заданную интервалом [ x, x + δx ]. Так как модуль импульса электрона сохраняется (потенциальное рассеяние), то поперечный импульс равен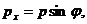 
где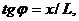 
и поэтому индивидуальная ошибка наблюдения поперечного импульса оказывается равной
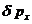~ pδφ. Считая, что δx ~ d, находим δφ ~ d/L, и поэтому 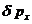~ pd/L. С другой стороны, pd ~ ħ, чтобы дифракция была наблюдаема, откуда 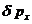~ ħ /L, и поэтому для индивидуальных наблюдений справедливо соотношение неточностей:
δx 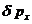~ δx ħ /L << ħ, (2.20)
поскольку всегда можно считать, что δx << L.
На первый взгляд, соотношение (2.20) представляется противоречащим соотношению неопределенностей (2.19). Однако это не так, поскольку в (2.19) входят статистические ошибки в серии измерений Δx ~ d, Δp ~ p, а в (2.20)- индивидуальные ошибки, относящиеся к одиночному наблюдению, кстати, уже выполненному. Поэтому-то Гейзенберг особо подчеркивал, что соотношение неопределенностей (2.19) нельзя относить к прошлому [5].
Таким образом, все предсказания квантовой механики, в том числе и соотношение (2.19), относятся к предстоящим измерениям, к будущему, - и в этом согласны между собой сторонники обеих интерпретаций, признавая, что эти предсказания носят только вероятностный характер. Различие в позициях обнаруживается, если поставить вопрос иначе. Именно: если каждый отдельный электрон попадает на экране в какое-то определенное место и в индивидуальных наблюдениях соотношение неопределенностей Гейзенберга не соблюдается, то возможно ли другое описание микроявлений, отличающееся от квантовой механики и использующее совсем другие переменные, которые позволят получить дополнительную информацию об индивидуальных микропроцессах?
Сторонники копенгагенской интерпретации отвечают на этот вопрос отрицательно, считая, что квантовая механика дает максимально полное описание микромира. Если же следовать статистической интерпретации, то построение таких более широких теорий возможно, и в их рамках можно будет получить более детальное описание индивидуальных микроявлений, использующее новые переменные, которые получили название скрытых параметров. Совершенно ясно, что новая теория должна быть похожа на статистическую механику, и после усреднения по скрытым параметрам должны восстанавливаться все результаты квантовой теории.
Спор между сторонниками двух указанных позиций, начавшийся сразу же после появления теории Шредингера, продолжается до сих пор. С обеих сторон выдвигаются различные аргументы в пользу той или иной точки зрения. Цель настоящей статьи как раз и состоит в том, чтобы по возможности выяснить позиции сторон. В частности, Эйнштейн
предлагал различные мысленные эксперименты, пытаясь показать неполноту квантового описания. В свою очередь, Бор, опровергая аргументы Эйнштейна, выдвинул принцип дополнительности, который является концентрированным выражением дуализма «волна - частица» и опирается на бесспорное положение о том, что всякое наблюдение предполагает использование классического прибора.
Согласно принципу дополнительности Бора, существуют два типа взаимно исключающих друг друга установок, предназначенных для измерения несовместных наблюдаемых, задаваемых некоммутирующими операторами. Это означает, что для измерения пространственных характеристик изучаемой системы (координат) необходимо использовать один тип приборов, а для измерения импульсов, сопряженных с отмеченными координатами, - совсем другой тип приборов. Указанное свойство квантовых измерений явно отражается в структуре (2.8) волновой функции системы. Общепринят специальный термин «контекстуальность», или относительность к средствам наблюдения, характеризующий это свойство [7].
Аргументы Эйнштейна, которыми он пытался убедить Бора в неполноте квантового описания, были чрезвычайно простыми. Например, рассматривая радиоактивный α –распад ядра, он отмечал, что волновая функция, характеризующая распад, не содержит никакой информации о времени распада отдельного ядра, хотя ясно, что это событие действительно имеет место в какой-то момент, и поэтому нет никаких оснований для запрета какого-либо более полного описания этого явления.
Очень нагляден следующий мысленный эксперимент, убеждающий в непротиворечивости позиции Эйнштейна. Пусть электрон помещен в некоторый ящик с непроницаемыми стенками, и после введения двойной перегородки ящик разделяется на две части A и B, которые переносятся соответственно в Париж и Токио. Допустим, что в Токио ящик B открывается, и обнаруживается, что электрона в нем нет. Совершенно ясно, что электрон всегда находился в ящике A. Однако квантовая механика никакой информации о локализации электрона до момента вскрытия ящика B нам не дает. Более того, согласно Бору, в момент вскрытия волновая функция электрона мгновенно стягивается в область A (Париж), исчезая в области B (Токио). Происходит так называемая редукция волнового пакета, его мгновенное стягивание, которое не может быть связано ни с какими физическими процессами. Считая подобное описание неприемлемым в рамках последовательной физической теории, Эйнштейн предполагал, что возможно построение другой, отличной от квантовой механики теории, которая предоставит недостающую информацию об индивидуальных процессах. Условно называя такую теорию теорией со скрытыми параметрами, попробуем выяснить ее возможные взаимосвязи с квантовой механикой. Однако вначале, слегка нарушив хронологию событий, уместно будет более подробно остановиться еще на одной попытке Эйнштейна представить максимально строгое доказательство неполноты квантовой механики.
Речь идет о знаменитой статье Эйнштейна, Подольского и Розена (ЭПР) [8], в которой был сформулирован так называемый «парадокс ЭПР». Поскольку предполагается, что все обсуждаемые теоретические построения имеют отношение к действительности, сначала принимаются два определения, касающиеся понятий полноты физической теории и элемента физической реальности:
Определение 1. Для того чтобы некоторая теория была полной, необходимо и достаточно,
чтобы каждый элемент физической реальности (из области применимости теории) имел соответствие в теории.
Определение 2. Достаточным условием для отождествления некоторого элемента физической реальности является следующее: «Если, никак не возмущая систему, можно с определенностью, т. е. с вероятностью, равной единице, предсказать значение некоторой физической величины, то существует элемент физической реальности, отвечающий этой физической величине».
После этого авторы рассматривают некоторый мысленный эксперимент, анализ которого, по их мнению, и приводит к выводу о неполноте квантовой механики. Оригинальный опыт ЭПР представляется слишком громоздким, и поэтому будет рассмотрена более простая его версия, предложенная Д. Бомом [9]. Предположим, что система, состоящая из двух частиц со спином ½, находится в метастабильном состоянии со спином ноль. Соответствующая спиновая волновая функция может быть представлена в виде линейной комбинации одночастичных спиновых функций:
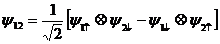, (2.21)
и с ее помощью можно вычислить спиновый коррелятор
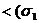a) 
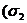b)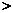 
= - (ab), (2.22)
где единичные векторы a и b определяют направления проектирования спинов соответственно первой и второй частиц. Состояния типа (2.21) получили название запутанных состояний (entangled states).
В результате распада