ВЕРОЯТНОСТИ СЛОЖНЫХ СОБЫТИЙ

 

Для вычисления вероятностей сложных событий используются следующие факты теории вероятностей. Если события A и B несовместны (т.е. не могут произойти одновременно), то вероятность их суммы равна сумме их вероятностей

P(A + B) = P(A) + P(B). (4.1)

Если же события A и B совместны, то

P(A + B) = P(A) + P(B) − P(AB). (4.2)

Если события A и B независимы (т.е. вероятность одного из событий не зависит от появления или не появления другого), то вероятность произведения событий равна произведению их вероятностей

P(AB) = P (A) P(B). (4.3)

Если же события А и В зависимы, то вместо формулы (4.3) используется формула

P (AB) = P (A) P (B / A) = P (B) P (A / B), (4.4)

где P(A / B) и P(B / A) - условные вероятности событий A и B соответственно.

При этом под условной вероятностью P(A / B) события A понимают вероятность события A, вычисленную при условии, что событие B уже произошло. Аналогично понимается вероятность P(B / A).

Формулы (4.1)-(4.4) легко обобщаются на случай n событий 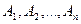. Так, если события 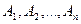попарно несовместны (т.е. любые два события из группы не могут происходить одновременно), то

P(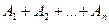) = P (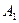) + P (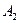) +... + P (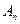). ( 4.5)

Если события 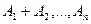- независимы в совокупности (т.е. появление одного события не зависит от появления или не появления остальных), то

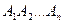P (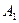) = P () P (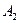) ⋅... ⋅ P (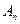). (4.6)

Если же события не являются независимыми в совокупности, то вместо формулы (4.6) используется формула

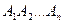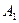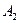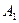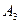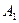
P () = P () P ( / ) P ( / 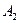) ⋅... ⋅ P ( 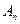/ 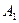⋅... ⋅ 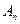). (4.7)

Правила сложения и умножения вероятностей (формулы (4.1) - (4.7) редко применяются порознь, обычно они используются вместе. Наиболее типична следующая схема: событие А, вероятность которого надо найти, представляется в виде суммы попарно несовместных событий

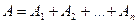(4.8)

Далее используется формула (4.1) или (4.5), в результате чего нахождение Р(А) сводится к отысканию суммы вероятностей P (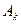), к=1, 2,..., n. Для этого каждое слагаемое в формуле (4.8) представляется в виде произведений событий, и для отыскания P (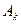) используется одна из формул (4.3),(4.4),(4.6),(4.7).

Следует помнить, что при отыскании вероятности появления "хотя бы одного события" обычно переходят к противоположному событию "не появилось ни одно событие" и используют формулу

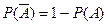, (4.9)

где А - событие, состоящее в том, что появилось хотя бы одно событие из некоторой группы событий 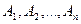, событие 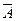состоит в том, что не появилось ни одного события из этой группы.

Пример 1. Вероятность обнаружения самолета за один обзор локатора равна 0,2. Найти вероятность того, что локатор обнаружит самолетровно на пятом обзоре.

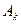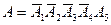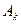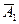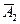Решение. Введем события = {локатор обнаруживает самолет на k-м обзоре}, k=1,2,3,4,5; А = {самолет обнаружен}. Тогда имеем . Так как события (к=1,2,3,4,5) независимы в совокупности, то P(A) = P (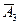) P () P (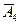) P () P (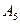). Но P(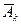) = 1 − 0,2 = 0,8, k = 1,2,3,4. Поэтому P(A) = 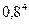⋅ 0,2 = 0,082.

Ответ: 0,082.

Пример 2. По каналу связи передаются три сообщения. Каждое из них независимо от других искажается с вероятностью 0,2. Найти вероятности следующих событий: A = {все сообщения переданы без искажений}, B = {все события искажены}, C = {хотя бы одно сообщение искажено}, D = {ровно одно сообщение передано без искажений}, F = {ров-

но два сообщения переданы без искажений}.

Решение. Введем в рассмотрение вспомогательные события: 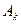= {k-е сообщение передано без искажений}, 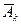={k-ое сообщение искажено}, k=1, 2, 3. Согласно условию P (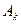) = 1 − 0,2 = 0,8.

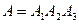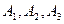Так как , и независимы в совокупности, то

P(A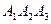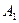) = P () = P(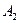) P () P (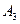) = = 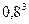0,512.

Далее, так как B = 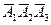, то

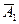P (B) = P (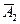) P () P (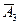) = = 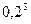0,008.

Событие C = , поэтому P (C) = 1 − P(A) = 1 − 0,512 = 0,488.

Событие D можно представить следующим образом D = + + ,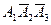

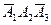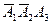причем слагаемые 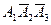, , 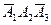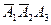− попарно несовместные события. Поэтому на основании формулы (4.5) получаем

P(D) = P(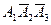) + P (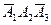) + P (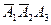). (4.10)

Далее по формуле (4.6)

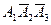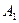P () = P(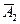) P() P(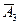) = 0,8 ⋅ 0,2 ⋅ 0,2 = 0,032,

P(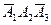) = 0,2 ⋅ 0,8 ⋅ 0,2 = 0,032, P(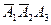) = 0,2 ⋅ 0,2 ⋅ 0,8 = 0,032.

Подставим найденные значения в формулу (4.10), получим P(D)=0,096.

Наконец, событие F представим так

F = + + .

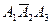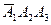Проводя рассуждения, подобные изложенным выше, из последней формулы получим

P(F) = 0,8 ⋅ 0,8 ⋅ 0,2 + 0,8 ⋅ 0,2 ⋅ 0,8 + 0,2 ⋅ 0,8 ⋅ 0,8 = 0,384.

Ответ: 0,512; 0,008; 0,488; 0,096; 0,384.

Пример 3. На рис. 4.1 приведена схема соединения элементов. Считая, что отказы элементов независимы в совокупности, найти вероятность безотказной работы схемы, если вероятности отказов элементов равны соответственно 0,1; 0,2; 0,05.

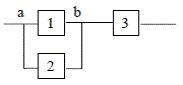
Pис. 4.1.

 

Решение. Введем в рассмотрение событие: A ={схема работает безотказно}, 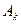= {к-й блок работает безотказно}, к=1,2,3; В={цепь а-b работает безотказно}. Тогда 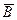= {цепь a − b отказала}. Отказ цепи а-b возможен, если только одновременно отказывают элементы 1 и 2, значит, 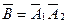. Теперь по формуле (4.3)

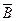P(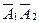) = P(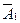) = P () P (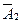) = 0,1 ⋅ 0,2 = 0,02.

Отсюда по формуле вероятности противоположного события

P(B) = 1 − P (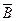) = 1 − 0,98 = 0,02.

Схема на рис. 4.1 работает, если одновременно работают цепь a-b и

элемент 3, значит, 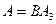. По формуле (4.3)

P(A) = P(B) P (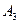) = 0,98 ⋅ (1 − 0,05) = 0,931.

Ответ: 0,931.

Пример 4. Опыт состоит в последовательном подбрасывании монеты два раза. Рассматриваются события: A = {первый раз выпадает герб}, B = {второй раз выпадает герб}, С = {герб выпадает хотя бы один раз}, D = {цифра выпадает хотя бы один раз}. Определить, зависимы или независимы пары событий: А и В, А и D, В и С, С и D.

Решение. Так как P(B) = P(A / B) = 0,5, то события А и В независимы.

Tак как 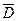={ни разу не выпадает цифра}, то 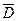= AB, следовательно,

P(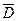) = 0,5 ⋅ 0,5 = 0,25, P (D) = 1 − 0,25 = 0,75.

Событие: выпадение цифры хотя бы один раз при условии, что первый раз уже появился герб, возможно только в том случае, если второй раз появится цифра, что может произойти с вероятностью 0,5. Значит, Р(D/А) =0,5. Итак, P(D / A) ≠ P (D), поэтому события А и D зависимы.

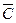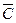Так как ={не выпадает ни одного герба}, то . Следовательно, P () = 0,5 ⋅ 0,5 = 0,25 и P(C) = 1 − 0,25 = 0,75. Событие: выпадение хотя бы одного герба при условии, что герб выпадает при втором подбрасывании, происходит всегда. Значит, P(C / B) = 1. Итак, P(C / D) ≠ P (C), поэтому события B и C зависимы.

Произведение событий CD состоит в одновременном появлении хотя бы один раз и герба, и цифры, что возможно только в том случае, если и герб, и цифра выпадают по одному разу, т.е. CD = 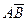+ 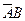. Находим P(CD) = P(A) P ( 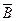) + P( 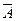) P (B) = 0,5 ⋅ 0,5 + 0,5 ⋅ 0,5 = 0,5. Кроме того, Р(С) =0,75, Р(D) =0,75. Поэтому согласно (4.4)

P(D / C) = P(CD) / P (C) = 0,5 / 0,75 = 2 / 3 ≠ P(D).

Значит, события C и D зависимы.

Пример 5. В урне a белых и b черных шаров. Наугад вынимается два шара. Найти вероятности следующих событий: A = {вынуты шары разного цвета}, В = {вынуты шары одного цвета}.

Решение. Заметим, прежде всего, что эту задачу можно было бы решить на основе классической вероятности (см. раздел 2). Мы же будем решать задачу с помощью теорем сложения и умножения вероятностей. Введем вспомогательные события: 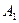= {первый вынутый шар белый}, 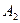= {второй вынутый шар белый}.

Так как событие A состоит в вынимании одного белого и одного черного шаров, то 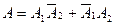. По формулам (4.1), (4.4)

P(A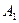) = P(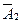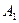) P( 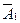/ ) + P() P (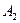 / 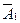). (4.11)

Находим

,

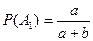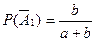
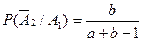
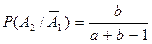
и подставим в формулу (4.11). Получим

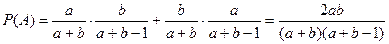
Далее, так как B = 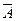, то

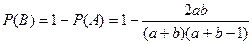
Ответ: 2ab /((a + b)(a + b − 1)), 1 − 2ab /((a + b)(a + b − 1)).

Пример 6. На 10 карточках написаны буквы: A, А, А, А, А, Р, Р, Р, Д, Д. Наугад берется 5 карточек и прикладывается одна к другой слева направо. Какова вероятность того, что случайно будет сложено слово РАДАР?

Решение. Чтобы сложить слово РАДАР, нужно, чтобы первой была взята буква Р (вероятность ее взять равна 3/10, так как имеются 3 буквы Р из 10), второй – буква А (вероятность ее взять равна 5/9, так как имеются 5 букв А среди оставшихся 9 карточек), третьей - буква Д (вероятность ее взять составляет 2/8, так как имеются 2 буквы Д среди

оставшихся 8 карточек), четвертой - снова буква А (с вероятностью 4/7, так как остались 4 буквы А среди оставшихся 7 карточек), пятой - снова буква Р (с вероятностью 2/6, так как остались две буквы Р среди оставшихся 6 карточек). Таким образом,

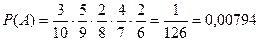
Ответ: 0,00794.

 

4.1. Производится стрельба в мишень до первого попадания. Вероятность поражения мишени при одном выстреле равна 0,2. Найти вероятность того, что будет произведено 6 выстрелов.

4.2. Ведется пристрелка орудия по цели. Вероятность попадания в цель при первом выстреле равна 0,7, при последующих выстрелах эта вероятность каждый раз увеличивается на 0,05. Какова вероятность того, что цель будет поражена лишь третьим выстрелом?

4.3. Брошены три игральные кости. Найти вероятность следующих событий: A = {на всех костях выпало по 5 очков}, B = {на всех костях выпало одно и то же число очков.}

4.4. Два стрелка, для которых вероятность попадания в цель равна соответственно 0,7 и 0,8, производят по выстрелу. Определить вероятности событий: A ={цель поражена двумя пулями}, B = {цель поражена одной пулей}, C = {цель поражена хотя бы одной пулей}.

4.5. Три студента делают некоторый расчет. Вероятность ошибиться для первого студента составляет 0,1, для второго - 0,15, для третьего - 0,2. Найти вероятности следующих событий: A = {все студенты выполнили расчет верно}, B = {только два студента выполнили верно расчет}, C = {хотя бы один студент допустил ошибку в расчете}.

4.6. По рации передаются три закодированных сообщения. Вероятность ошибки при расшифровке каждого сообщения составляет 0,3. Найти вероятности следующих событий: A = {все сообщения расшифрованы верно}, B = {одно сообщение расшифровано с шибкой}, C = {с ошибкой расшифровано не менее двух сообщений}.

4.7. ОТК отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех взятых изделий: а) только одно высшего сорта; б) два высшего сорта; в) хотя бы одно высшего сорта.

4.8. Вероятность выхода из строя каждого двигателя трех моторного самолета равна p. Самолет может продолжать полет, если работает хотя бы один двигатель. Какова вероятность аварии?

4.9. Самолет терпит аварию, если отказали оба двигателя, или вышла из строя система управления, или вышли из строя системы навигации. Найти вероятность аварии самолета, если вероятность выхода из строя каждого двигателя составляет 0,005, системы управления - 0,001, систем навигации - 0,0002.

4.10. В ящике лежат 12 красных, 8 зеленых, 10 синих шаров. Наудачу вынимается два шара. Найти вероятность того, что будут вынуты шары разного цвета.

4.11. Студент знает 40 из 60 вопросов программы. Экзаменационный билет состоит из 3 вопросов, отобранных случайным образом. Какова вероятность того, что студент знает не менее двух вопросов билета?

4.12. На 10 карточках написаны буквы: А, А, А, А, А, А, М, М, М, М.Ребенок наугад вытаскивает одну за другой 4 карточки и прикладывает их друг к другу слева направо. Какова вероятность того, что он случайно сложит слово МАМА?

4.13. Слово МАТЕМАТИКА разрезается на буквы. Буквы перемешиваются и снова складываются слева направо. Найти вероятность того, что снова получится слово МАТЕМАТИКА.

4.14. Слово АККЛИМАТИЗАЦИЯ разрезается на буквы, которые тщательно перемешиваются. Вытаскиваются наугад 5 букв и прикладываются одна к другой слева направо. Какова вероятность сложить слова: а) акция; б) клика; в) казак?