ВЫСШАЯ МАТЕМАТИКА
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
методические рекомендации
по изучению дисциплины и контрольные задания
Минск
Авторы-составители:
ст. препод. C.C.Третьякевич, доцент В.А.Фигурин
Данное пособие предназначено для использования студентами заочного отделения Международного государственного экологического университета им. А.Д. Сахарова по специальности “Информационные системы и технологии в экологии” при изучении курса “Теория вероятностей и математическая статистика”.
© Международный государственный экологический университет им. А.Д. Сахарова, 2007
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ. 5
1. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ.. 6
2. ЛИТЕРАТУРА.. 7
3. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ.. 8
4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ.. 9
Тема 1. Основные понятия теории вероятностей. 9
Тема 2. Случайные величины.. 12
Тема 3. Основные законы распределения случайных величин. 18
Тема 4. Системы случайных величин. 22
Тема 5. Закон больших чисел и предельные теоремы.. 30
Тема 6. Случайные процессы.. 33
Тема 7.Основные понятия математической статистики. 37
Тема 8. Оценка закона распределения. 38
Тема 9. Оценка моментов и параметров распределения. 42
Тема 10. Оценка параметров общей линейной модели измерений. 49
Тема 11. Проверка статистических гипотез. 53
5. Задания контрольной работы.. 58
ПРЕДИСЛОВИЕ
Среди разделов высшей математики, завоевавших прочное место в науке, технике и других областях знаний, важную роль играет теория вероятностей и математическая статистика.
Статистические методы описания явлений уже давно стали неотъемлемой частью аппарата теоретической физики. Одновременно статистика стала важным инструментом и в экспериментальных исследованиях, связанных прежде всего с обработкой результатов наблюдений, которые по своей природе представляют собой случайные величины. Лишь только статистический анализ позволяет сделать надежные выводы о многих изучаемых явлениях.
Если первоначально основное использование статистических методов обработки результатов измерений заключалось в отыскании средних значений и их погрешностей, то усложнение экспериментов потребовало искать поддержки статистическими методами решения более сложных задач, связанных, например, с оцениванием параметров и проверкой гипотез.
В отличие от математической статистики, устанавливающей закономерности случайных явлений, теория вероятностей занимается изучением закономерностей, присущих случайным явлениям, и является математическим аппаратом математической статистики. В свою очередь, математическая статистика оказывает влияние на развитие теории вероятностей. Таким образом, теория вероятностей и математическая статистика – две неразрывно связанные области науки.
Цель дисциплины – изучение основных закономерностей, присущих случайным величинам, и установление закономерности случайных явлений на основании систематизации обработки экспериментальных результатов.
1. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Данное пособие ставит своей целью оказание помощи студентам заочного отделения в организации их самостоятельной работы по овладению системой знаний, умений и навыков в объеме действующей программы.
Эта работа требует не только большого упорства, но и умения, без которого затрата сил и времени не дает нужно эффекта. Читать, понимать прочитанное и применять его практически – вот что составляет суть умения работать с учебными пособиями.
Прежде всего необходимо ознакомиться с содержанием программы дисциплины. Хотя учебное пособие Вам и рекомендовано, более того, оно полностью соответствует программе дисциплины, целесообразно также обращаться к другим учебным пособиям, в которых, возможно, есть ответы на не совсем понятые вами вопросы.
Ведите краткий конспект изучаемой дисциплины, который должен содержать главным образом определения, свойства распределений, числовые характеристики случайных величин, виды распределений и т.д.
Учитесь самоконтролю. Для студента-заочника это важнейшая форма проверки понимания и усвоения материала. Помните, что учебник (учебное пособие) нужно не просто читать и запоминать прочитанное, а изучать. Выработайте в себе привычку систематической самостоятельной работы.
Задания контрольной работы следует выполнять самостоятельно и лишь после того, как проработан соответствующий теоретический материал и рассмотрены примеры задач. Задания необходимо выполнять по мере изучения материала.
2. ЛИТЕРАТУРА
Основная
1. Фигурин В.А., Оболонкин В.В. Теория вероятностей и математическая статистика: Учебное пособие. – Мн.: ООО “Новое знание”, 2000.
Дополнительная
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для студентов втузов. – М.: Высшая школа, 1999 (можно любое издание)
3. ТРЕБОВАНИЯ
К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Студент должен выполнить работу, строго придерживаясь следующих требований.
1. Контрольная работа выполняется по варианту, номер которого совпадает с последней цифрой номера зачетной книжки студента.
2. Контрольная работа выполняется в отдельной тетради школьного формата чернилами (пастой) любого цвета, кроме красного. На страницах оставляются поля не менее 3 см для замечаний рецензента.
3. На обложке тетради должны быть четко написаны: фамилия, имя, отчество студента; номер зачетной книжки; специальность; номер группы; факультет; название дисциплины; дата отсылки работы в университет; адрес студента.
4. Решения задач располагать в порядке заданий.
5. Перед решением каждой задачи необходимо переписать ее условие.
6. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.
7. В конце работы следует указать литературу, которая была использована при выполнении заданий.
После получения прорецензированной работы студент должен исправить в ней допущенные ошибки и недочеты и представить ее на повторное рецензирование. Поэтому рекомендуется в конце тетради оставлять несколько чистых листов для внесения исправлений и дополнений в соответствии с указанием рецензента.
Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.
4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
Тема 1. Основные понятия теории вероятностей
Случайные события. Классическое определение вероятности. Статистическое определение вероятности. Аксиоматическое построение теории вероятностей. Сумма и произведение событий. Теорема сложения вероятностей. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса.
Сначала изучите материал, изложенный в главе 1[1]. Затем ответьте на вопросы и выполните задания для самопроверки. Внимательно разберите решения приведенных примеров. Решите задачи, предлагаемые для самостоятельного решения.
При изучении материала обратите внимание на следующее.
1. Несколько несовместных событий образуют полную группу событий, если в результате испытания появится хотя бы одно из них.
2. Сумма вероятностей несовместных событий, составляющих полную группу, равна единице.
3. События называются несовместными, если появление одного из них исключает появление других в одном и том же испытании, т.е. они не могут произойти одновременно. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
4. Для двух совместных событий
P(A + B) = P(A) + P(B) – P(AB).
5. Событие А называется статистически зависимым от события В, если вероятность события А зависит от того, осуществилось или не осуществилось событие В:
Р(А/В).
6. События А и В независимы, если Р(АВ) = Р(А)∙Р(В). Это имеет место и для большего числа событий.
7. Формула полной вероятности позволяет вычислить вероятность события А, которое может наступить тогда и только тогда, когда наступило одно из событий (гипотез) Hi, i = 1, …, n, при этом вероятности гипотез P(Hi) (их называют априорными вероятностями) и условные вероятности P(A/Hi) (их называют апостериорными) известны.
8. Формула Байеса применяется для вычисления условной вероятности P(Hi/A) гипотезы Hi после испытания, при котором произошло событие А. Другими словами, формулы Байеса (их число равно числу гипотез) позволяют переоценить (дать другую оценку) вероятности гипотез, принятые до испытания, по результатам уже проведенного испытания.
Вопросы и задания для самопроверки
1. Какое событие называют достоверным, какое –- невозможным?
2. Какое событие называется случайным?
3. Какие события называются несовместными?
4.Приведите классическое определение вероятности события.
5.Приведите статистическое определение вероятности события.
6. Какое событие называется суммой двух событий?
7. Какое событие называется произведением двух событий?
8. Сформулируйте теорему сложения вероятностей.
9.Что такое условная вероятность?
10. Сформулируйте теорему умножения вероятностей.
11. Запишите формулу полной вероятности.
12. Запишите формулу Байеса.
Примеры решения задач
Пример 1. Бросают два игральных кубика. Какова вероятность того, что сумма выпавших очков равна 7?
Решение. Каждый из кубиков может упасть шестью различными способами. Тогда два кубика могут упасть 6∙6=36 различными способами. Каждому такому способу соответствует событие, которое является исходом бросания двух кубиков. В силу симметричности кубиков все эти события равновозможны и образуют полную группу несовместных событий. Поэтому число исходов бросания двух кубиков n=36. Сумма очков равная 7 будет иметь место, когда на гранях кубика выпадет соответственно 1 и 6, 2 и 5, 3 и 4, 4 и 3, 5 и 2, 6 и 1. Всего 6 благоприятных исходов. Тогда по классическому определению Р(А)=m/n=6/36=1/6.
Пример 2. Отдел технического контроля проверяет на стандартность по двум параметрам серию изделий. Было установлено, что у 8 из 25 изделий не выдержан только первый параметр, у 6 изделий - только второй, а у 3 изделий не выдержаны оба параметра. Наудачу берется одно из изделий. Какова вероятность того, что оно не удовлетворяет стандарту?
Решение. Рассмотрим следующие события: А –- «у изделия не выдержан первый параметр», В – «у изделия не выдержан второй параметр», С – «изделие не удовлетворяет стандарту». Событию АВ, состоящему в том, что у взятого изделия не выдержаны оба параметра, благоприятствуют три исхода. Событию А благоприятствуют 8+3=11 исходов, а событию В благоприятствуют 6+3=9 исходов. Тогда по теореме сложения вероятностей для двух совместных событий
Р(С) = Р(А + В)=Р(А) + Р(В) – Р(АВ) = 11/25 + 9/25 – 3/25 = 17/25.
Пример 3. Среди пациентов туберкулезного диспансера 15% принадлежат к первой категории больных, 66% – ко второй и 19% – к третьей. Вероятности возникновения заболевания в зависимости от категории больных равны соответственно 0,12; 0,09; 0,2. Найти вероятность возникновения заболевания у наугад выбранного пациента диспансера.
Решение. Воспользуемся формулой полной вероятности:
Р(А)= 
.
Применительно к задаче вероятность P(H1) гипотезы о том, что пациенты принадлежат к первой категории больных, равна 0,15. Аналогично Р(Н2) = 0,66 и Р(Н3) = 0,19. Условные вероятности возникновения заболевания у каждой категории больных равны: Р(А/Н1) = 0,12; Р(А/Н2) = 0,09; Р(А/Н3) = 0,2.
Таким образом,
Р(А) = 0,15∙0,12 + 0,66∙0,09 + 0,19∙0,2 = 0,1154.
Задачи для самостоятельного решения
Задача 1. Бросают два игральных кубика. Какова вероятность того, что сумма выпавших очков будет не более трех?
Ответ: 1/12.
Задача 2. Бросается игральный кубик. Какова вероятность того, что выпадет четное и меньшее 5 число очков?
Ответ: 1/3.
Задача 3. Среди пациентов туберкулезного диспансера 15% принадлежат к первой категории больных, 66% – ко второй и 19% – к третьей. Вероятности возникновения заболевания в зависимости от категории больных равны соответственно 0,12; 0,09; 0,2. Найти вероятность принадлежности к третьей категории больных пациента, у которого обнаружено заболевание.
Ответ: 0,3293.
Тема 2. Случайные величины
Понятие случайной величины. Описание случайных величин. Функция распределения. Числовые характеристики случайных величин. Характеристические функции. Преобразование законов распределения и моментов.
Сначала изучите материал, изложенный в главе 2 [1]. Затем ответьте на вопросы и выполните задания для самопроверки. Внимательно разберите решения приведенных примеров. Из контрольной работы выполните первое, второе, третье и четвертое задания своего варианта.
Изучаемый материал является очень важным для понимания последующих тем, поэтому особое внимание уделите следующему.
1. Способам описания случайных величин (законам распределения, плотностям вероятности, функциям распределения, их свойствам).
2. Математическому ожиданию случайной величины и его свойствам.
3. Дисперсии случайной величины и ее свойствам.
4. В условии нормировки закона распределения и в определении числовых характеристик пределы от минус до плюс бесконечности приведены для общности. В реальности эти пределы соответствуют граничным значениям, принимаемым случайной величиной.
5. Определению особых значений случайной величины, таких как квантиль и процентная точка. Эти значения играют в статистике первостепенную роль, поэтому твердо уясните то, о чем будет идти речь ниже.
Квантилем порядка р (или р-квантилем) непрерывной случайной величины Х называется такое возможное значение хр этой величины, для которого вероятность события Х<хp равна заданной величине вероятности р, т. е.
Р(Х<хp) = 
,
где F(хp)- значение функции распределения при х=хр.
Именно уравнение
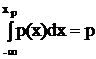
следует решить, чтобы найти квантиль хр.
В случае дискретной случайной величины р-квантиль определяется как любое число хр, лежащее между двумя возможными значениями хi(p) и хi(p)+1, такое что F(хi(p)) < р, но F(хi(p)+1) ≥ р.
Кроме квантиля пользуются также процентной точкой распределения. Под процентной точкой порядка q (или q-процентной точкой) случайной величины понимаетсятакое ее возможное значение хq ; для которого вероятность события X>хq равна q, т. е.
Для дискретных случайных величин это определение корректируется аналогично тому, как это делается при определении квантиля.
Из определения квантиля и процентной точки вытекает простое связывающее их соотношение:
квантиль порядка р = процентная точка порядка 1 – р.
Иногда порядок процентной точки выражают в процентах.
Для примера рассмотрим непрерывную случайную величину с распределением р(х) = 1/2, 0 ≤ х ≤ 2, которое называется равномерным распределением и имеет следующий вид:
Найдем квантиль порядка 0,25 такого распределения. Составим уравнение
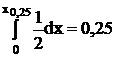или 
.
Отсюда х0,25 = 2∙0,25 = 0,5. Обратите внимание, что площадь под плотностью вероятности от х = 0 до х0,5 = 0,5, как видно из рисунка, равна 0,25.
Найдем процентную точку порядка 0,75. Составим уравнение
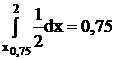или 
.
Отсюда х0,75 = 0,5. В этом случае площадь под плотностью вероятности от 0,5 до 2, равна 0,75.
Вопросы и задания для самопроверки
1. Дайте определение случайной величины.
2. Что называют законом распределения дискретной случайной величины?
3. Что понимают под законом распределения непрерывной случайной величины?
4. Каким свойством обладает плотность вероятности случайной величины?
5. Дайте определение функции распределения случайной величины. Какими свойствами она обладает?
6. Как связаны между собой плотность вероятности и функции распределения?
7. Как, зная плотность вероятности, найти вероятность попадания случайной величины в заданный интервал?
8. Изобразите закон распределения случайной величины Х- числа очков, выпадающих на верхней грани при бросании правильной игральной кости.
9. Дайте определение математического ожидания дискретной случайной величины.
10. Что называют математическим ожиданием непрерывной случайной величины?
11. Перечислите свойства математического ожидания случайной величины.
12. Что такое мода и медиана случайной величины?
13. Дайте определение дисперсии случайной величины.
14. Перечислите основные свойства дисперсии.
15. Что такое начальные и центральные моменты случайной величины? Как они определяются?
16. Дайте определение квантиля порядка р случайной величины.
17. Как найти закон распределения случайной величины, являющейся функцией дискретной случайной величины?
18. Как найти плотность вероятности случайной величины, являющейся функцией непрерывной случайной величины?
19. Как найти моменты функционально преобразованной случайной величины?
Примеры решения задач
Пример 1. Плотность вероятности случайной величины Х имеет вид
р(х) = С(1+х)-3, х ≥ 0.
Необходимо: 1) определить значение постоянной С; 2) найти функцию распределения; 3) изобразить графики плотности вероятности и функции распределения; 4) найти вероятность того, что случайная величина не превысит значения, равного единице.
Решение. 1) Постоянную С можно найти из условия нормировки плотности вероятности
. 
Имеем:
.
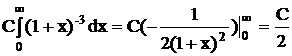Приравняв полученное значение единице, получим С = 2.
Следовательно,
р(х) = 2(1+х)-3, х ≥ 0.
2) Находим функцию распределения:
.
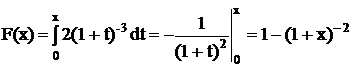Итак,
3) Графики плотности вероятности функции распределения строим, задавая случайной величине Х некоторые конкретные значения, например 0; 0,25; 0,5; 0,75; 1. В результате получим:
4) Вероятность того, что случайная величина не превысит значения, равного единице, можно найти двумя способами:
или
.
Если функция распределения вычислена, то легче использовать второй способ:
Р(0 ≤ Х ≤1)= 1 – (1 + 1)-2 – 0= 1 – ¼ = 0,75.
Пример 2. Закон распределения дискретной случайной величины х имеет вид
| хi | ||||
| рi | 1/8 | 3/8 | 3/8 | 1/8 |
Необходимо найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины.
Решение. По определению математического ожидания дискретной случайной величины имеем:
По определению дисперсии:
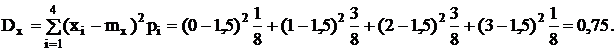
Для нахождения дисперсии можно также воспользоваться эквивалентной формулой:
Среднее квадратическое отклонение σ является положительным квадратным корнем из дисперсии:
.
Пример 3. Случайная величина Х имеет плотность вероятности
р(х) = х/2, 0 ≤ х ≤ 2.
Требуется найти математическое ожидание и дисперсию случайной величины.
Решение. Математическое ожидание и дисперсия случайной величины в общем случае определяется формулами:
Применительно к задаче имеем:
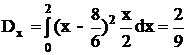
Вычисление дисперсии можно значительно упростить, применяя формулу
Dx= M[X2] – mx2.
.
Пример 4. Случайная величина Х имеет плотность вероятности
рх(х)= 1/π, -π/2 < х < π/2.
Необходимо найти плотность вероятности случайной величины Y= sinX.
Решение. В интервале (-π/2, π/2) функция y= sin x однозначная, следовательно существует однозначная обратная функция x= arcsin y. Плотность вероятности величины Y находится по формуле
Поскольку
, то
, -1<y<1.
Пример 5. Случайная величина Х распределена равномерно в интервале (-π/2, π/2).
Необходимо найти плотность вероятности случайной величины
Y = cosХ.
Решение. В интервале (-π/2, π/2) функция y= cos x является двузначной, обратные ей функции
х1= -arccos y, х2= arccos y.
Поэтому
Следовательно,
0<y<1.
Тема 3. Основные законы
распределения случайных величин
Биномиальное распределение. Распределение Пуассона. Экспоненциальное распределение. Равномерное распределение. Нормальное распределение.
Сначала изучите материал, изложенный в главе 3 [1]. Затем ответьте на вопросы и выполните задания для самопроверки. Внимательно разберите решение приведенных примеров.
При изучении материала обратите внимание на следующее.
1. Последовательность независимых испытаний по схеме Бернулли удовлетворяет следующим условиям:
1) при каждом испытании различают лишь два исхода: появление некоторого события А, либо появление противоположного ему события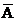 
;
2) испытания являются независимыми, т. е. вероятность события А в n-ом испытании не зависит от исходов всех испытаний до n-го;
3) вероятность наступления события А во всех испытаниях постоянна и равна Р(А) = p. Вероятность события Р(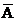) = 1-р = q.
Приведем несколько примеров реальных испытаний, которые в той или иной степени «вписываются» в такую последовательность испытаний:
- последовательное подбрасывание N раз симметричной монеты (здесь событием А может являться появление «герба» с вероятностью р = 1/2) или последовательное бросание N раз игрального кубика (здесь событием А можно считать, например, появление шестерки с вероятностью р = 1/6). Эти две реальные схемы испытаний являются примером идеального соответствия схеме испытаний Бернулли;
- последовательность N выстрелов стрелка по мишени можно лишь приближенно рассматривать как схему испытаний Бернулли, так как независимость результатов стрельбы может нарушаться либо из-за «пристрелок» спортсмена, либо вследствие его утомляемости.
2. При N→∞ и Np = λ биномиальное распределение сходится к распределению Пуассона. Однако в ряде задач распределение Пуассона получается как точное. Общая схема формирования пуассоновской случайной величины - это число событий, наступающих за одинаковые промежутки времени, при этом наступление события в определенном промежутке времени не зависит от того, сколько раз и в какие моменты времени оно наступило в прошлом промежутке, и не влияет на наступление событий в последующие промежутки, а испытания проводятся в стационарном режиме.
3. Нормальное распределение - самое важное в теории и практике статистических исследований по нескольким причинам. Прежде всего, многие наблюдаемые случайные величины можно успешно описать нормальным распределением или, по крайней мере, нормальное распределение может стать первым приближением к их описанию. Не существует таких распределений, которые были бы в точности нормальными, поскольку значения, принимаемые нормальной случайной величиной, лежат в диапазоне от минус до плюс бесконечности.
Общий механизм формирования нормально распределенной случайной величины состоит в следующем. Значения случайной величины формируются под действием большого числа независимых случайных факторов, причем сила действия каждого фактора мала и не может превалировать среди остальных, а характер действия аддитивный, т. е. при воздействии случайного фактора на величину a получается величина a+∆, где остаток ∆ относительно мал и равновероятен по знаку.
4. Интеграл вероятности - это функция распределения нормированной нормально распределенной случайной величины. С его помощью можно находить вероятность попадания значений нормально распределенной случайной величины в заданный интервал. В качестве примера найдем вероятность попадания значений случайной величины с нулевым математическим ожиданием и единичной дисперсией в интервал от -1 до 1.
По таблице1 приложения [1] находим что для z = 1 Ф(1) = 0,8413. Поскольку Ф(-z) = 1-Ф(z), то Ф(-1) = 0,1587. Отсюда
Р(-1≤X≤1) = Ф(1) - Ф(-1) = 0,8413 - 0,1587 = 0,6828.
5. По таблице интеграла вероятности можно также находить квантили стандартного нормального распределения. Для примера найдем квантиль порядка 0,95. Это значение вероятности нужно найти внутри таблицы, а затем определить, при каком z оно получается. В таблице точного значения 0,95 нет, есть близкие к нему 0,94950 и 0,95053, которые имеют место соответственно при z = 1,64 и z = 1,65. Путем интерполяции получим z0,95 = 1,645.
Вопросы и задания для самопроверки
1. Опишите последовательность испытаний по схеме Бернулли.
2. Запишите биномиальный закон распределения. Какими параметрами он описывается? Каков смысл этих параметров?
3. Чему равны математическое ожидание и дисперсия биномиального распределения?
4. Запишите закон распределения Пуассона. От какого параметра он зависит? Каков смысл этого параметра?
5. Постройте плотность вероятности экспоненциально распределенной случайной величины с математическим ожиданием равным единице.
6. Запишите выражение для плотности вероятности нормального распределения. Сколькими параметрами оно описывается? Какой смысл они имеют?
7. Какое распределение называется равномерным? Чему равен третий центральный момент этого распределения?
8. Какое распределение называется стандартным нормальным распределением?
9. Что представляет собой интеграл вероятности?
10. Используя таблицу интеграла вероятности, найдите вероятность того, что нормально распределенная случайная величина с математическим ожиданием 5 и дисперсией 4 будет принимать значения в интервале от 3 до 7.
11. Чему равен квантиль порядка 0,5 стандартного нормального распределения?
Примеры решения задач
Пример 1. Случайная величина Х имеет биномиальное распределение с параметрами N=3 p=0,3. Вычислить вероятность того, что случайная величина примет значение большее нуля.
Решение. Случайная величина может принимать значения 0, 1, 2 и 3. Вероятность Р(Х>0) равна сумме вероятностей Р(Х=1), Р(Х=2) и Р(Х=3). Однако, можно в данном случае поступить иначе - вычислить Р(Х=0), тогда Р(Х>0) =1 - Р(Х=0).
По формуле биномиального распределения находим:
,
откуда Р(Х>0) = 0,488.
Пример 2. Случайная величина Х имеет нормальный закон распределения с нулевым математическим ожиданием. Вероятность нахождения случайной величины в интервале (-0,3;0,3) равна 0,5.
Необходимо найти значение среднеквадратического отклонения σ случайной величины.
Решение. Воспользовавшись тем, что (см. стр. 59[1]) для нормального распределения
применительно к условиям задачи будем иметь:
Итак, необходимо решить относительно σ уравнение:
или 
По таблице интеграла вероятности находим квантиль порядка 0,75. Он равен 0,675.
Отсюда 0,3/σ = 0,675 и
Пример 3. Случайная величина Х имеет нормальное распределение с параметрами m=5 и σ2=4. Чему равны квантили распределения порядка 0,5 и 0,67?
Решение. Квантили находим из уравнения
В первом случае 
Интеграл вероятности равен 0,5 при значении аргумента равном нулю. Отсюда
х0,5-5 = 0 и х0,5 = 5.
Получили вполне очевидный результат, поскольку нормальное распределение симметрично относительно математического ожидания, которое совпадает с медианой распределения, а медиана – квантиль порядка 0,5.
Аналогично,
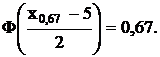
По таблице интеграла вероятности находим значение аргумента, при котором интеграл вероятности равен 0,67. Это значение равно 0,44. Отсюда
и 
Задачи для самостоятельного решения
Задача 1. Случайная величина Х имеет нормальное распределение с параметрами m=0 и σ2=1. Что больше: P(-0,5 ≤ X ≤ -0,1) или Р(1 ≤ X ≤ 2)?
Ответ: первая вероятность больше.
Задача 2. Случайная величина Х имеет распределение Пуассона с параметром λ=1. Найти вероятность того, что случайная величина принимает значения большие единицы.
Ответ: 2/е.
Тема 4. Системы случайных величин
Законы распределения двумерных случайных величин. Условные распределения двух случайных величин. Числовые характеристики двумерных законов распределения. Корреляция. Числовые характеристики n-мерных случайных величин. Функциональные преобразования двумерных плотностей вероятностей. Гамма-распределение. Распределение хи-квадрат. Двумерное нормальное распределение.
Сначала изучите материал, изложенный в главе 4 [1]. Затем ответьте на вопросы и выполните задания для самопроверки. Внимательно разберите решения приведенных примеров. Решите задачи для самостоятельного решения. Из контрольной работы выполните 5-е задание своего варианта.
При изучении материала обратите особое внимание на следующее.
Как и для одномерных случайных величин, на законы распределения многомерных случайных величин налагается условие нормировки.
Одномерные функции распределения и плотности вероятности могут быть найдены через двумерные.
Условный закон распределения – закон распределения одной случайной величины при условии, что другая случайная величина приняла определенное значение. Для нахождения условной плотности вероятности случайной величины X, образующей со случайной величиной Y двумерную систему, можно воспользоваться формулой:
.
1. Если совместный закон распределения (плотность вероятности) системы случайных величин можно представить в виде произведения законов распределения каждой случайной величины, то такие случайные величины являются независимыми.
2. Основными числовыми характеристиками системы случайных величин являются математические ожидания и дисперсии каждой случайной величины, а также корреляционные моменты (или коэффициенты корреляции) между каждой парой случайных величин. Если система состоит из двух случайных величин X и Y, то имеем математические ожидания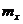 
и 
, дисперсии 
и 
и корреляционный момент 
.
3. Коэффициент корреляции между двумя случайными величинами X и Y определяет степень линейной вероятностной зависимости между этими величинами.
4. Независимые случайные величины всегда некоррелированы, зависимые – могут быть как коррелированными, так и некоррелированными.
5. При нахождении дисперсии или суммы случайных величин необходимо учитывать корреляцию между ними.
6. Композиция законов распределения – задача нахождения плотности вероятности суммы нескольких независимых случайных величин по известным законам распределения слагаемых. Эта задача может быть решена путем последовательного вычисления интегралов свертки или с помощью аппарата характеристических функций.
7. Распределение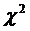 
(хи-квадрат) описывает распределение суммы квадратов k независимых случайных величин, каждая из которых имеет стандартное нормальное распределение. Число k называется числом степеней свободы распределения .
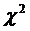Вопросы и задания для самопроверки
1. Как выглядит закон распределения дискретной двумерной случайной величины, представленный таблицей?
2. Как, зная закон распределения двумерной случайной величины (X,Y), найти законы распределения случайных величин X и Y?
3. Какими свойствами обладает функция распределения двумерной случайной величины?
4. Какими свойствами обладает плотность вероятности двумерной случайной величины?
5. Как, зная двумерную функцию распределения, найти одномерную функцию распределения.
6. Какое условие является необходимым и достаточным для того, чтобы две дискретные величины были независимыми?
7. Как проверить независимость двух непрерывных случайных величин?
8. Какими числовыми характеристиками описываются двумерные случайные величины?
9. Двумерная случайная величина характеризуется двумя математическими ожиданиями или одним?
10. Дайте определение корреляционного момента двумерной случайной величины. Что этот момент характеризует?
11. Что такое коэффициент корреляции? В каком диапазоне лежат его значения?
12. Если коэффициент корреляции равен нулю, означает ли это, что случайные величины независимы?
13. Чему равно математическое ожидание произведения двух зависимых случайных величин?
14. Чему равны дисперсии суммы и разности двух зависимых случайных величин?
15. Какими основными числовыми характеристиками описываются n-мерные случайные величины?
16. Напишите формулу для интеграла свертки двух плотностей вероятностей. Что эта формула позволяет находить?
17. Распределение какой случайной величины описывается гамма-распределением?
18. Что называют случайной величиной 
? Какое распределение она имеет?
19. Какие две случайные величины называются совместно нормальными?
20. Будут ли две совместно нормальные случайные величины независимыми, если они некоррелированы?
Примеры решения задач
Пример 1. Закон распределения двумерной дискретной случайной величины (X,Y) задан таблицей
| 
| ||
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-12-29 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |