Свойства математического ожидания

Лекция 8

Центральные моменты

Введем понятие центрированной случайной величины = X - М (X) и будем рассматривать моменты отклонения X - М (X).

Определение Центральным моментом порядка k случайной вели­чины X называют математическое ожидание величины :

Первый центральный момент равен нулю 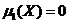. Докажем для дискретной случайной величины.

Второй центральный момент наиболее важен и называется дисперсией и обозначается D(X)

- для дискретной случайной величины, (8.1)

- для непрерывной случайной величины. (8.2)

Получим формулу, выражающую D(X) через математическое ожидание. Покажем для дискретной случайной величины

(8.3)

Так же выводятся другие соотношения, связывающие началь­ные и центральные моменты.

Таким образом, для центральных моментов случайной величины X справедливы формулы:

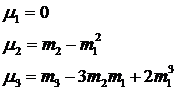
Вероятностный смысл математического ожидания

Пусть произведено n испытаний, в которых слу­чайная величина X приняла 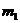раз значение , 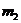раз значение ,..., 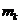раз значение , причем 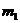+ +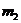...+ 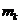= n. Тогда сумма всех значений, принятых X, равна

+ +... + .

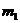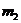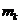Найдем среднее арифметическое всех значений, при­нятых случайной величиной, для чего разделим найден­ную сумму на общее число испытаний:

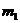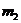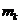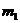= ( + +... + )/n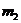= /n + 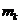/n +... + /n=

=

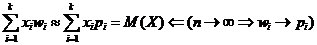
здесь относительная частота.

Вывод: вероятностный смысл полученного результата таков - математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифмети­ческому наблюдаемых значений случайной величины.

Замечание 1. Математическое ожидание характеризует расположение распределения и поэтому его часто называют центром распреде­ления. Этот термин заимствован из механики: если массы 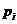расположены в точках с абсциссами причем = 1, то абсцисса центра тяжести .

Итак, математическое ожидание есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы — их вероятностям.

Замечание 2. Происхождение термина «математическое ожи­дание» связано с начальным периодом возникновения теории вероят­ностей (XVI — XVII вв.), когда область ее применения ограничива­лась азартными играми. Игрока интересовало среднее значение ожи­даемого выигрыша, или, иными словами, математическое ожидание выигрыша.

Свойства математического ожидания

Доказательства будем проводить для дискретных случайных величин.

Свойство 1. Математическое ожидание по­стоянной величины равно самой постоянной:

.

X = С , М (С) = С 1= С.

Свойство 2. Постоянный множитель можно выно­сить за знак математического ожидания:

Пусть случайная величина X задана законом распределения вероятностей . Тогда

Замечание 3. Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие воз­можные значения приняла другая величина. В противном случае случайные величины зависимы. Несколько случайных величин назы­вают взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.

Замечание 4. Определим произведение независимых случай­ных величин X и Y как случайную величину XY, возможные зна­чения которой равны произведениям каждого возможного значения X на каждое возможное значение Y; вероятности возможных значе­ний произведения XY равны произведениям вероятностей возможных значений сомножителей. Например, если вероятность возможного значения равна 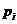, вероятность возможного значения равна , то вероятность возможного значения равна .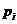

Заметим, что некоторые произведения x,y могут оказаться рав­ными между собой. В этом случае вероятность возможного значения произведения равна сумме соответствующих вероятностей.

Свойство 3. Математическое ожидание произведе­ния двух независимых случайных величин равно произведе­нию их математических ожиданий:

.

Пусть независимые случайные величины X и Y заданы своими законами распределения вероятностей:

X Y

P Q

Составим все значения, которые может принимать случайная величина XY. Для этого перемножим все воз­можные значения X на каждое возможное значение Y; в итоге получим, соответствующие вероятности :

Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:

Итак, M(XY) = M(X)M(Y).

Следствие. Математическое ожидание произведе­ния нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

Например, для трех случайных величин имеем:

М (XYZ) = М (XYZ) = М (XY) M(Z) = M (X) М (Y) M (Z).

Для произвольного числа случайных величин дока­зательство проводится методом индукции.

Следующее ниже свойство справедливо как для неза­висимых, так и для зависимых случайных величин.

Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

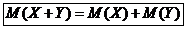
Пусть независимые случайные величины X и Y заданы своими законами распределения вероятностей:

X Y

P Q

Составим все возможные значения величины X + У. Для этого к каждому возможному значению X прибавим каждое возможное значение У; получим . Для простоты предположим, что эти возможные значения различны (если это не так, то дока­зательство проводится аналогично), и обозначим их ве­роятности соответственно через .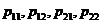

Математическое ожидание величины Х + Y равно сумме произведений возможных значений на их вероятности:

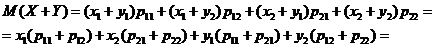
Следствие. M(X+Y+Z) = M(X) + M(Y) + M(Z).