Введение
Система MATLAB, обладает большими возможностями программирования и комплексной визуализации результатов инженерных расчетов и научных исследований. В этой связи покажем применение богатых возможностей MATLAB в решении задач вычислительной математики. Развитие многих наук привело исследователей к необходимости численного решения различных проблем, т. е. применению численных методов. Численные методы создаются и исследуются высококвалифицированными специалистами - математиками и, как в системе MATLAB, предлагаются для применения в виде готового инструмента. Поэтому задачей методических указаний является изложение основных идей численных методов и ознакомление с последовательностью применения численных процессов в современных компьютерных системах.
Программы, реализующие какой-либо численный метод, необходимо записывать в М-файл. Если не дать имени М-файлу, то он запишется при выполнении программы в рабочую папку под именем Untitled (Безымянный). Такой ситуации следует избегать для исключения появления множества файлов с неопределенным именем. Рассмотрим решение различных проблем вычислительной математики, имеющих важное значение при изучении различных наук.
Список лабораторных работ
Табулирование функций
Данная задача широко используется в экологии, теплофизике и других дисциплинах. Обычно функции, описывающие какой-либо процесс, весьма громоздки и создание таблиц их значений требует большого объема вычислений.
Рассмотрим два случая табулирования функции:
· С постоянным шагом изменения аргументов.
· С произвольным набором значений аргумента.
Алгоритм реализуется путем организации какого-либо цикла.
Пример 1.Вычислить
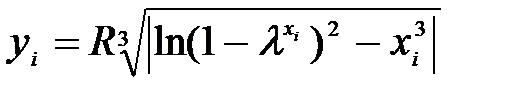 ,
,
при R = 4.28 • 10-2; λ = 2.87;
xi изменяется с шагом Δх = 2; хn = 2; хk = 10.
Введем обозначение λ → lа = 2.87.
Протокол программы:
R = 4.28е-02; lа = 2.87;
% Задается начальное значение х, шаг dх и конечное значение х
х = 2.0: 2.0: 10.0;

% Для вывода значения у в конце строки символ; не ставится!
В окне команд появляются после нажатия кнопки выполнить значения функции y, которые затем можно скопировать в какой-либо файл.
Результаты вычислений:
ans =
2.0000 4.0000 6.0000 8.0000 10.0000
0.0682 0.1634 0.2517 0.3386 0.4250
Пример 2.Вычислить и вывести на экран значения функции
 ;
;
При х1 = 12.8; х2 = 23.4;х3 = 27.2; х4 = 17.8;х5 = 16.3; х6 = 14.9; а = 1.35; b = 0.98.
Данную задачу можно программировать, не изменяя обозначения переменных. Цикл организуется для одномерного массива.
Протокол программы:
а = 1.35; b = 0.98; х (1) = 12.8; х (2) = 23.4; х (3) = 27.2; х (4) = 17.8; х (5) = 16.3; х (6) = 14.9;
form = 1:6; 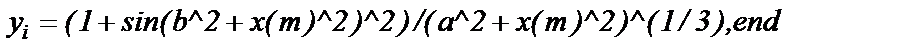 ;
;
% В конце строки вычисления функции у символ; не ставится.
| y= | 0.3609 |
| y= | 0.2327 |
| y= | 0.1473 |
| y= | 0.1800 |
| y= | 0.1771 |
| y= | 0.1658 |
Данные вычислений можно вывести в виде таблицы, если использовать запись [ х; у ] без точки с запятой или [ х у ].
Варианты заданий
Составить программу вычисления значений функции у, для значений аргумента xi. Данные взять из таблицы 1.
Таблица 1
| № п/п | Функция y1 = f(xi) | Задача А | Задача В | ||||||||
| a | b | хн | хк | Δх | x1 | x2 | хз | х4 | x5 | ||

| - | 2.5 | 1.28 | 3.28 | 0.4 | 1.1 | 2.4 | 3.6 | 1.7 | 3.9 | |

| 1.35 | 0.98 | 1.14 | 4.24 | 0.62 | 0.35 | 1.28 | 3.51 | 5.21 | 4.16 | |
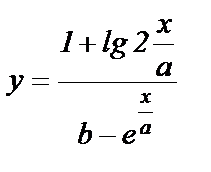
| 2.0 | 0.95 | 1.25 | 2.75 | 0.3 | 2.2 | 3.78 | 4.51 | 6.58 | 1.2 | |
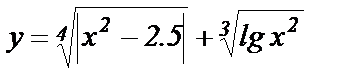
| - | - | 1.25 | 3.25 | 0.4 | 1.84 | 2.71 | 3.81 | 4.56 | 5.62 | |

| -2.5 | 3.4 | 3.5 | 6.5 | 0.6 | 2.89 | 3.54 | 5.21 | 6.28 | 3.48 | |
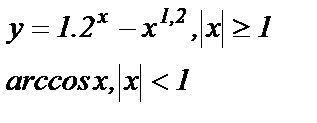
| - | - | 0.2 | 2.2 | 0.4 | 0.1 | 0.9 | 1.2 | 1.5 | 2.3 | |

| 0.4 | 0.8 | 3.2 | 6.2 | 0.6 | 4.48 | 3.56 | 2.78 | 5.28 | 3.21 | |

| 1.2 | 0.48 | 0.7 | 2.2 | 0.3 | 0.25 | 0.36 | 0.56 | 0.94 | 1.28 | |

| 1.1 | 0.09 | 1.2 | 2.2 | 0.2 | 1.21 | 1.76 | 2.53 | 3.48 | 4.52 | |

| 0.05 | 0.06 | 0.2 | 0.95 | 0.15 | 0.15 | 0.26 | 0.37 | 0.48 | 0.56 | |
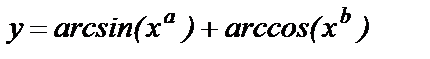
| 2.0 | 3.0 | 0.11 | 0.36 | 0.05 | 0.08 | 0.26 | 0.35 | 0.41 | 0.53 | |

| 1.6 | - | 1.2 | 3.7 | 0.5 | 1.28 | 1.36 | 2.47 | 3.68 | 4.56 | |

| 4.1 | 2.7 | 1.2 | 5.2 | 0.8 | 1.9 | 2.15 | 2.34 | 2.73 | 3.16 | |
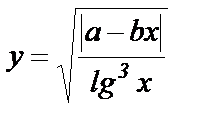
| 7.2 | 4.2 | 1.81 | 5.31 | 0.7 | 2.4 | 2.8 | 3.9 | 4.7 | 3.16 | |
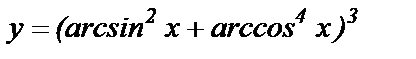
| - | - | 0.26 | 0.66 | 0.08 | 0.1 | 0.35 | 0.4 | 0.55 | 0.6 | |

| 2.0 | 1.1 | 0.08 | 1.08 | 0.2 | 0.1 | 0.3 | 0.4 | 0.45 | 0.65 | |
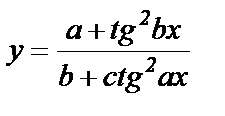
| 0.1 | 0.5 | 0.15 | 1.37 | 0.25 | 0.2 | 0.3 | 0.44 | 0.6 | 0.56 | |

| 2.5 | 4.6 | 1.1 | 3.6 | 0.5 | 1.2 | 1.28 | 1.36 | 1.46 | 2.35 | |
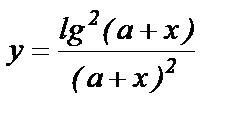
| 2.0 | - | 1.2 | 4.2 | 0.6 | 1.16 | 1.32 | 1.47 | 1.65 | 1.93 | |
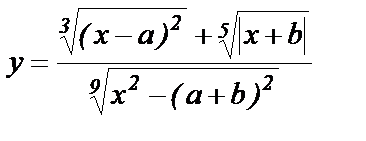
| 0.8 | 0.4 | 1.23 | 7.23 | 1.2 | 1.88 | 2.26 | 3.84 | 4.55 | -6.21 | |
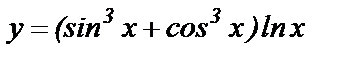
| - | - | 0.11 | 0.36 | 0.05 | 0.2 | 0.3 | 0.38 | 0.43 | 0.57 | |

| 2.25 | - | 1.2 | 2.7 | 0.3 | 1.31 | 1.39 | 1.44 | 1.56 | 1.92 | |

| 4.1 | 2.7 | 1.5 | 3.5 | 0.4 | 1.9 | 2.15 | 2.34 | 2.74 | 3.16 | |
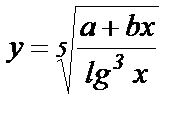
| 7.2 | 1.3 | 1.56 | 4.71 | 0.63 | 2.4 | 2.8 | 3.9 | 4.7 | 3.16 | |

| - | - | 0.22 | 0.92 | 0.14 | 0.1 | 0.35 | 0.4 | 0.55 | 0.6 | |

| 2.0 | 4.1 | 0.77 | 1.77 | 0.2 | 1.24 | 1.38 | 2.38 | 3.21 | 0.68 | |

| 0.1 | 0.5 | 0.33 | 1.23 | 0.18 | 0.5 | 0.36 | 0.40 | 0.62 | 0.78 | |

| 2.5 | 4.6 | 1.15 | 3.05 | 0.38 | 1.2 | 1.36 | 1.57 | 1.93 | 2.25 | |

| 2.0 | 1.08 | 1.88 | 0.16 | 1.16 | 1.35 | 1.48 | 1.52 | 1.96 | ||

| 0.8 | 0.4 | 1.42 | 3.62 | 0.44 | 1.6 | 1.81 | 2.24 | 2.65 | 3.38 |
Решение систем линейных алгебраических уравнений методом исключения Гаусса
К решению систем линейных уравнений сводятся многочисленные практические задачи, например различные краевые задачи для обыкновенных и в частных производных дифференциальных уравнений. Можно с полным основанием утверждать, что данная проблема является одной из самых распространенных и важных задач вычислительной математики.
Пусть задана система п линейных алгебраических уравнений с п неизвестными:
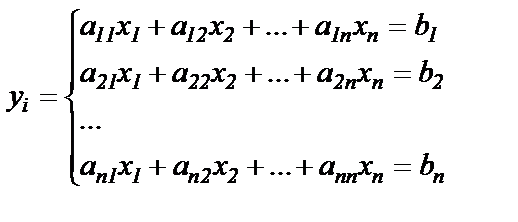 (1)
(1)
Система уравнений (1) в матричной форме представляется следующим образом:
АХ = В, (2)
где А - квадратная матрица коэффициентов, размером п х п строк и столбцов;
X - вектор-столбец неизвестных;
В - вектор-столбец правых частей.
Систему уравнений (2) можно решить различными методами. Один из наиболее простых и эффективных методов является метод исключения Гаусса и его модификации. Алгоритм метода основан на приведении матрицы А к треугольному виду (прямой ход) и последовательном вычислении неизвестных (обратный ход). Эти процедуры можно выполнять над невыраженными матрицами, в противном случае метод Гаусса неприменим.
Недостатком метода является накапливание погрешностей в процессе округления, поэтому метод Гаусса без выбора главных элементов используется обычно для решения сравнительно небольших ( п < 100) систем уравнений с плотно заполненной матрицей и не близким к нулю определителем. Если матрица А сильно разрежена, а ее определитель не близок к нулю, то метод Гаусса пригоден для решения больших систем уравнений. В MATLAB имеется обширный арсенал методов решения систем уравнений (2) методом исключения Гаусса. Для этого применяются следующие операторы
/ - правое деление;
\ - левое деление;
^ - 1-возведение в степень -1;
inv(А) - обращение матрицы А.
Выражения
X = В/А
X = В*А^-1
X = В*inv(А)
X = А\В
дают решения ряда систем линейных уравнений АХ = В, где А - матрица размером m х n, В- матрица размером п х к. Более сложные случаи решения систем уравнений (2) с плохо обусловленной матрицей А освещены в специальной литературе.
Пример 3.
Решить систему 4-х линейных уравнений:
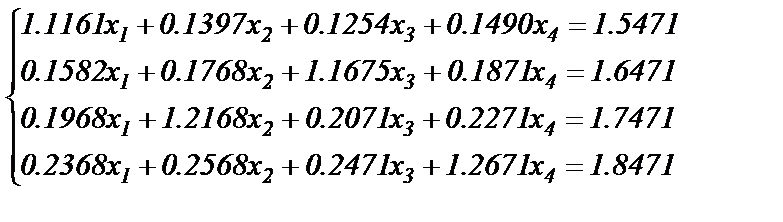
Протокол программы (в М-файле)
а = [1.1161 0.1397 0.1254 0.1490;
0.1582 0.1768 1.1675 0.1871;
0.1968 1.2168 0.2071 0.2271;
0.2368 0.2568 0.2471 1.2671];
b = [1.5471; 1.6471; 1.7471; 1.8471];
Х4 = а\b
Эта программа выдает решение заданной системы с помощью четвертого оператора в виде матрицы - столбца
Х4 =
1.0406
0.9351
0.9870
0.8813
Внимание. В М-файле матрица а набирается по строкам, а элементыматрицы правых частей b отделяются символом;, т. е. тоже набираются по строкам. Решение другими операторами системы уравнений (2) требует набора матрицы а по столбцам, а элементы правых частей b отделяются только пробелом !
| а | = [1.1161 | 0.1582 | 0.1968 | 0.2368; |
| 0.1397 | 0.1768 | 1.2168 | 0.2568; | |
| 0.1254 | 1.1675 | 0.2071 | 0.2471; | |
| 0.1490 | 0.1871 | 0.2271 | 1.2671]; | |
| b | = [1.5471 | 1.6471 | 1.7471 | 1.8471]; |
X1 =b/ а
Х2 = b*а ^ - 1
Х3 = b* inv(а)
Результаты решения
X1 =
1.0406 0.9351 0.9870 0.8813
Х2 =
1.0406 0.9351 0.9870 0.8813
X3 =
1.0406 0.9351 0.9870 0.8813
Варианты заданий. Решить систему линейных алгебраических уравнений с помощью 4-х операторов. Данные взять из таблицы 2.
Таблица 2
 ; ; 
|  ; ; 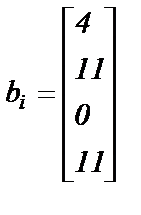
| ||
 ; ; 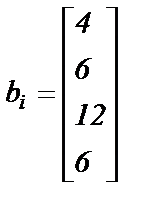
|  ; ; 
| ||
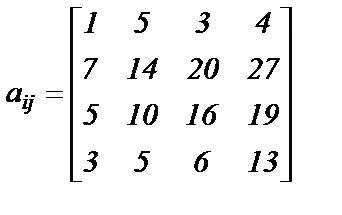 ; ; 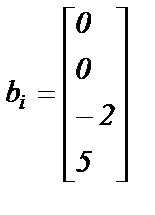
| 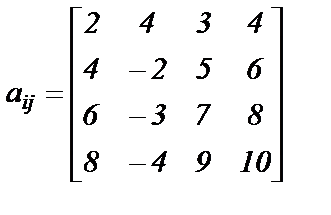 ; ; 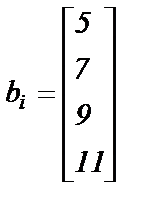
| ||
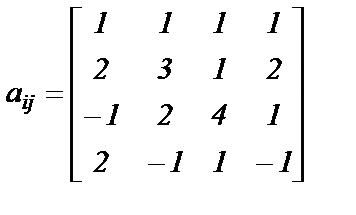 ; ; 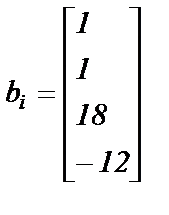
|  ; ; 
| ||
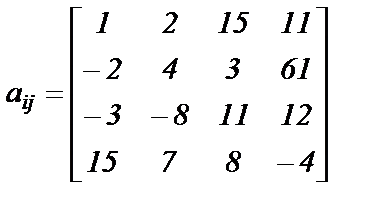 ; ; 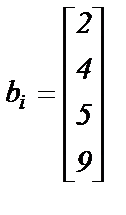
|  ; ; 
| ||
 ; ; 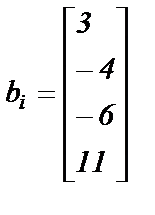
| 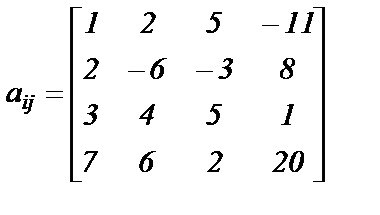 ; ; 
| ||
 ; ; 
| 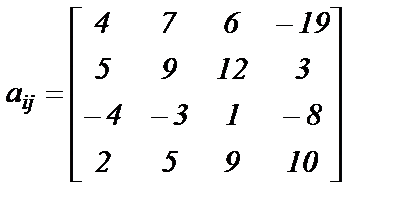 ; ; 
| ||
 ; ; 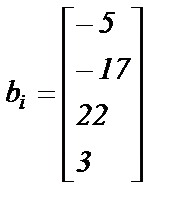
| 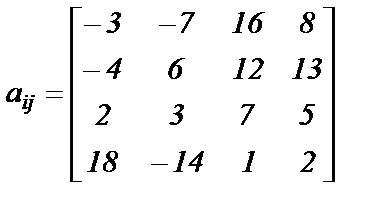 ; ; 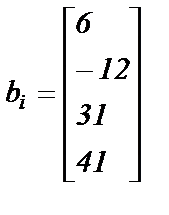
| ||
 ; ; 
|  ; ; 
| ||
 ; ; 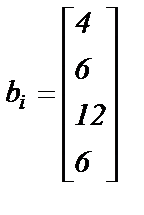
|  ; ; 
| ||
 ; ; 
|  ; ; 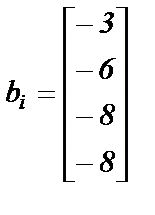
| ||
 ; ; 
|  ; ; 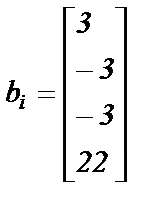
| ||
 ; ; 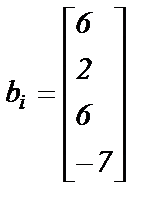
|  ; ; 
| ||
 ; ; 
|  ; ; 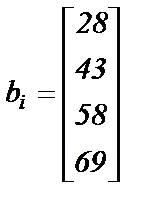
| ||
 ; ; 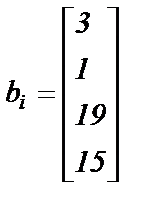
| 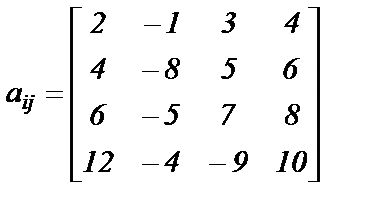 ; ; 
|
Аппроксимация функций
Одним из распространенных и практически важных случаев связи между аргументом и функцией является задание этой связи в виде некоторой таблицы {хi; уi}, например, экспериментальные данные. На практике часто приходится использовать табличные данные для приближенного вычисления у при любом значении аргумента х (из некоторой области). Этой цели служит задача о приближении (аппроксимации) функций: данную функцию f(х) требуется приближенно заменить некоторой функцией g(х) так, чтобы отклонение g(х) от f(х) в заданной области было наименьшим. Функция g(х) при этом называется аппроксимирующей. Если приближение строится на заданном дискретном множестве точек {хi}, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и др. При построении приближения на непрерывном множестве точек (например, на отрезке [ а, b ]) аппроксимация называется непрерывной или интегральной. MATLAB имеет мощные средства точечной и непрерывной аппроксимации с визуализацией результата. Рассмотрим наиболее важную точечную аппроксимацию (обработка экспериментальных данных).
Пример 4.Используя линейную и полиномиальную аппроксимации, получить эмпирические формулы для функции у=f(х), заданной в табличном виде:
| Xi | 0.75 | 1.50 | 2.25 | 3.00 | 3.75 |
| У i | 2.50 | 1.20 | 1.12 | 2.25 | 4.28 |
Оценить погрешность эмпирических формул.
Протокол программы. В окне команд набираются значения хi и уi. Далее
выполняется команда построения графика только узловых точек.
>>х = [0.75, 1.50, 2.25, 3.00, 3.75];
>>у = [2.50, 1.20, 1.12, 2.25, 4.28];
>> plot (х, у,' 0 ');
Появляется окно с символами ' 0 ' на месте узловых точек (рис. 1).

Рис. 1 – Отображение узловых точек
Внимание. Следует помнить, что при полиномиальной аппроксимации максимальная степень полинома на 1 меньше числа экспериментальных точек!
На панели инструментов окна графика узловых точек в меню Тоо1s исполняем команду Basic Fitting. Появляется окно Основной Монтаж. В этом окне птичкой отмечаются необходимые данные аппроксимации. В частности, можно задать следующие операции:
· показать уравнение аппроксимирующей функции у = g(х);
· выбрать метод подбора: cплайн интерполяции: эрмитовская интерполяция, линейный, квадратный, кубический и т.д.
В нашей задаче выбираем линейную и полиномиальную аппроксимации. В окне графика появляются соответствующие графики разноцветом и формулы аппроксимирующих функций (рис. 2).

Рис. 2 – Пример графиков линейной и полиноминальной интерполяций
Чтобы узнать погрешность аппроксимации, надо отметить птичкой параметр График остатка в окне Основной Монтаж, и Показать норму остатков. График погрешностей с нормами можно вынести в отдельное окно, или вместе с графиком и аппроксимирующих функций - суб-график. Норма погрешностей указывает на статистическую оценку среднеквадратической погрешности. Чем она меньше, тем точнее полученная аппроксимирующая функция у = у(х). В нашем примере:
Linear: norm of residuals (норма погрешности) = 2.1061
Quadratic: norm of residuals = 0.10736
Cubic: norm of residuals = 0.035857 4
4th degree: norm of residuals = 9.6305^-015.
График погрешностей можно выводить в виде диаграмм (зоны), линий (линии) или отдельных точек (фрагменты). Сам график погрешностей представляет собой зависимость разности g(х) - f(х) в условных точках, соединенных прямыми линиями.
Кроме линейной и полиномиальной аппроксимации можно выбрать сплайн-аппроксимацию - когда на каждом интервале приближения используется кубический полином с новыми коэффициентами. В этом случае нельзя получить выражение для аппроксимирующей функции, т. е. такая аппроксимация является неполной. Аналогичными свойствами обладает и Эрмитовая аппроксимация. Она имеет только графическую интерпретацию.
Варианты заданий. Получить эмпирические формулы и оценить их погрешность для функции у =f(х), заданной таблично. Данные взять из таблицы 3.
Таблица 3
| 1. | xi | -3 | -2 | -1 | ||||
| yi | -0.71 | -0.01 | 0.51 | 0.82 | 0.88 | 0.51 | 0.49 | |
| 2. | хi | -6.6 | -5.38 | -3.25 | -1.76 | 2.21 | 3.6 | 4.5 |
| yi | 2.89 | 1.41 | 0.29 | -0.41 | -0.69 | -0.7 | 1.2 | |
| 3. | хi | |||||||
| yi | -0.31 | 0.9 | 2.11 | 3.3 | 4.51 | 5.73 | 6.93 | |
| 4. | хi | -2 | -1 | |||||
| yi | 7.1 | 3.9 | 1.1 | 0.8 | 3.1 | 4.5 | 5.3 | |
| 5. | хi | -2 | -1 | -0.5 | 1.5 | 3.5 | ||
| yi | 5.9 | 2.8 | 2.1 | 3.2 | 6.1 | 7.6 | 4.3 | |
| 6. | хi | -3 | -2 | -1 | ||||
| yi | 3.1 | 0.9 | 0.9 | 2.8 | 7.1 | 6.5 | 4.1 | |
| 7. | хi | |||||||
| yi | 10.0 | 7.5 | 5.5 | 4.0 | 3.0 | 2.0 | 2.24 | |
| 8. | хi | -2 | -1 | 1.5 | 2.3 | 2.6 | 2.9 | |
| yi | 4.2 | 5.6 | 6.8 | 7.2 | 9.4 | 10.5 | 11.8 | |
| 9. | хi | 10.0 | 12.0 | 13.0 | 15.0 | 18.0 | 20.0 | 21.0 |
| yi | 0.66 | 0.89 | 1.24 | 1.36 | 1.56 | 1.76 | 1.92 | |
| 10. | хi | 22.0 | 24.0 | 27.0 | 30.0 | 31.0 | 35.0 | 40.0 |
| yi | 1.24 | 1.37 | 1.46 | 1.26 | 1.66 | 1.84 | 1.99 | |
| 11. | хi | -7.0 | -6.0 | -5.0 | -4.0 | -3.0 | -2.0 | -1.0 |
| yi | 22.6 | 24.7 | 25.6 | 24.6 | 23.5 | 21.8 | 19.3 | |
| 12. | хi | -25.0 | -23.0 | -21.0 | -18.0 | -17.2 | -15.4 | -14.0 |
| yi | 0.76 | 0.74 | 0.61 | 0.58 | 0.84 | 0.92 | 1.22 | |
| 13. | хi | -4.0 | -3.0 | -2.0 | -1.0 | 0.0 | 1.0 | 2.0 |
| yi | 1.71 | 1.56 | 1.24 | 1.36 | 1.78 | 2.21 | 4.31 | |
| 14. | хi | -22.0 | -20.0 | -18.0 | -16.0 | -14.0 | -12.0 | -10.0 |
| yi | -2.26 | -1.84 | -1.92 | -1.76 | -1.56 | -1.64 | -1.34 | |
| 15. | хi | 23.0 | 24.0 | 25.0 | 26.0 | 27.0 | 28.0 | 29.0 |
| yi | 1.26 | 1.37 | 1.44 | 1.56 | 1.15 | 1.28 | 1.06 | |
| 16. | хi | 30.0 | 33.0 | 35.0 | 37.0 | 39.0 | 41.0 | 43.0 |
| yi | -2.6 | -3.7 | -2.5 | -4.3 | -2.3 | -5.6 | -1.9 | |
| 17. | хi | 44.0 | 45.0 | 46.0 | 47.0 | 48.0 | 49.0 | 50.0 |
| yi | 2.24 | 3.46 | 5.36 | 1.89 | 1.76 | 1.54 | 2.12 | |
| 18. | хi | 52.0 | 54.0 | 56.0 | 58.0 | 60.0 | 62.0 | 64.0 |
| yi | -1.28 | -1.33 | -1.44 | -1.67 | -1.77 | -2.81 | -2.16 | |
| 19. | хi | 2.2 | 2.6 | 3.0 | 3.4 | 3.8 | 4.2 | 4.6 |
| yi | 1.88 | 1.65 | 1.61 | 1.73 | 1.56 | 1.24 | 1.99 | |
| 20. | хi | 5.1 | 5.3 | 5.5 | 5.7 | 5.9 | 6.1 | 6.3 |
| yi | -2.8 | -3.6 | -5.7 | -3.4 | -1.9 | -1.7 | -1.5 | |
| 21. | хi | 7.15 | 7.35 | 7.55 | 7.75 | 7.95 | 8.15 | 8.35 |
| yi | -2.2 | -3.6 | -1.7 | -2.8 | -1.6 | -4.5 | -2.2 | |
| 22. | хi | 9.1 | 9.2 | 9.3 | 9.4 | 9.5 | 9.6 | 9.7 |
| yi | 1.48 | 1.16 | 2.08 | 1.96 | 1.81 | 2.31 | 5.61 | |
| 23. | хi | -10.2 | -10.1 | -10.0 | -9.9 | -9.8 | -9.7 | -9.6 |
| yi | -6.5 | -7.8 | -10.2 | -5.4 | -4.6 | -9.5 | -10.3 | |
| 24. | хi | 11.0 | 14.0 | 17.0 | 20.0 | 23.0 | 26.0 | 29.0 |
| yi | 1.2 | 1.6 | 1.9 | 1.1 | 1.16 | 1.24 | 1.36 | |
| 25. | хi | -50.0 | -48.0 | -46.0 | -44.0 | -42.0 | -40.0 | -38.0 |
| yi | 1.23 | 1.32 | 1.57 | 1.19 | 1.16 | 1.10 | 2.28 | |
| 26. | хi | -36.0 | -34.0 | -32.0 | -30.0 | -28.0 | -26.0 | -24.0 |
| yi | 1.1 | 1.3 | 2.1 | 1.9 | 1.7 | 1.5 | 1.8 | |
| 27. | хi | 21.0 | 23.0 | 24.0 | 28.0 | 31.0 | 32.0 | 36.0 |
| yi | 1.24 | 1.37 | 1.56 | 1.64 | 1.84 | 1.26 | 1.14 | |
| 28. | хi | 10.0 | 13.0 | 17.0 | 22.0 | 28.0 | 35.0 | 43.0 |
| yi | 1.21 | 1.36 | 1.51 | 1.84 | 1.06 | 1.21 | 1.36 | |
| 29. | хi | -1.0 | 0.0 | 3.0 | 5.0 | 8.0 | 12.0 | 15.0 |
| yi | -2.1 | -3.6 | 1.2 | -4.3 | 1.8 | 2.6 | -0.2 | |
| 30. | хi | -8.0 | -7.0 | -5.0 | -3.0 | -1.0 | 2.0 | 5.0 |
| yi | 1.36 | 1.88 | 2.45 | -2.1 | -10.2 | -4.4 | 1.16 |