Знакомство с циклами
Численная оценка определенного интеграла
Задача вычисления интегралов возникает во многих областях прикладной математики. В большинстве случаев не удается найти аналитической формулы, т.е. выразить неопределенный интеграл в виде алгебраических и трансцендентных функций. Даже если аналитическая формула находится, то она получается настолько сложной, что вычислять интеграл с ее помощью труднее, чем другими способами. Распространенными являются также случаи, когда подынтегральная функция задается графиком или таблицей экспериментально полученных значений. В таких ситуациях используют различные методы численного интегрирования, которые основаны на том, что интеграл представляется в виде предела интегральной суммы (суммы площадей), и позволяют определить эту сумму с приемлемой точностью.
Пусть требуется вычислить определенный интеграл
1 
(1)
при условии, что a и b конечны и f(x) является непрерывной функцией x во всем интервале a < x < b. Значение интеграла I представляет собой площадь, ограниченную кривой f(x),осью x и прямыми x=a, x=b. Вычисление I проводится путем разбиения интервала от a до b на множество меньших интервалов, приближенным нахождением площади каждой полоски, получающейся при таком разбиении, и дальнейшем суммировании площадей этих полосок.
Суть методов численного интегрирования состоит в замене подынтегральной функции f(x) вспомогательной, интеграл от которой легко вычисляется в элементарных функциях. Обычно f(x) заменяется некоторым интерполяционным многочленом, что приводит к квадратурным формулам:
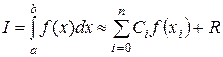2 
(2)
где xi - узлы интерполяции;
i - произвольный номер узла;
Ci - коэффициенты;
R - остаточный член или погрешность метода.
Не учет (отбрасывание) R приводит к погрешности усечения. К этим погрешностям в процессе вычислений добавляются погрешности округления.
Метод прямоугольников
Самыми простыми методами численного интегрирования являются методы прямоугольников. При этом непосредственно используется замена определенного интеграла интегральной суммой:
3 
(3)
4 
(4)
В качестве точек zi могут выбираться левые (
) или правые (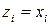
) границы элементарных отрезков. Обозначая 
получим формулы:
· метод “левых” прямоугольников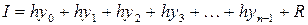 
;
· метод “правых” прямоугольников. 
.
· более точным является метод “средних” прямоугольников (метод средних), использующий значения функции в средних точках элементарных отрезков:
5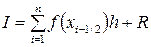 
(5)
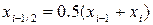6 
(6)
1 Рисунок 1 - Графическая интерпретация методов прямоугольников
Метод трапеций
Величина определенного интеграла численно равна площади фигуры, образованной графиком функции и осью абсцисс (геометрический смысл определенного интеграла). Следовательно, найти 
– это значит оценить площадь фигуры, ограниченной перпендикулярами, восстановленными к графику подынтегральной функции f(x) из точек a и b, расположенных на оси аргумента x.
Для решения задачи разобьем интервал [ a,b ] на n одинаковых участков. Длина каждого участка будет равна h=(b-a)/n (см. рис. 2).
2 Рисунок 2 – Графическое интерпретирование метода трапеций
Восстановим перпендикуляры из каждой точки до пересечения с графиком функции f(x). Если заменить полученные криволинейные фрагменты графика функции отрезками прямых, то тогда приближенно площадь фигуры, а, следовательно, и величина определенного интеграла оценивается как площадь всех полученных трапеций. Обозначим последовательно значения подынтегральных функций на концах отрезков f0, f1, f2,..., fn и подсчитаем площадь трапеций:
7 
(7)
В общем случае формула трапеций принимает вид:
8 
(8)
где fi – значение подынтегральной функции в точках разбиения интервала (a,b) на равные участки с шагом h; f0, fn – значения подынтегральной функции соответственно в точках a и b.
Метод Симпсона (параболы)
Геометрически иллюстрация формулы Симпсона состоит в том, что на каждом из сдвоенных частичных отрезков заменяем дугу данной кривой дугой графика квадратного трехчлена.
Разобьем отрезок интегрирования [a; b] на 2n равных частей длины 
. Обозначим точки разбиения 
. Значения функции f в точках xi обозначим yi, т.е. yi=f(xi). Тогда согласно методу Симпсона
9 
(9)
Примеры программ
Вычисление суммы ряда 
с помощью цикла FOR
Пример 1:
S = 0;
For i = 1:10
S = S + 1/i;
End
Пример 2:
For i = 1:10
S(i) = 1/i;
End
sum(S)
Вычисление суммы ряда с помощью цикла WHILE
S = 0;
i=1;
while i<=10
S = S + 1/i;
i = i + 1;
end
Вычисление суммы ряда без цикла
i=1:10;
s=1./i;
S=sum(s);
Задание 1
1) Вычислить определенный интеграл численными методами.
2) Выявить влияние числа n (количество подотрезков, на которые разбивается отрезок [a; b]) на точность вычисления определенного интеграла. В отчете привести числовые значения определенного интеграла при уменьшении n и увеличении.
3) Проверить результат вычисления определенного интеграла с помощью функции «int».
4) Метод реализовать в m-файле.
| № | Функция | Отрезок | Метод | Цикл | Переменная цикла | Подынтегральная функция |
| Y(t)= 10t3+5t2+2t+1 | [1;2] n=20 | Лев. Прям | for | аргумент | через m-функцию | |
| Y(t)=sin(t2) | [0;p/2] n=15 | Прав. Прям | While | номер итерации | в m-файле | |
| Y(t)=10-10exp(-0.05t) | [0;100] n=10 | Ср. прям | Без цикла | - | через m-функцию | |
| Y(t)=sin(2t)-cos(2t) | [p/6;p/2] n=25 | Трапеции | for | номер итерации | в m-файле | |
| Y(t)=sin(2t)+sin(4t)+sin(6t) | [0; p/5] n=15 | Симпсона | While | аргумент | через m-функцию | |
| Y(t)=arctg(t)+sin(2t) | [0;p/2] n=50 | Лев. Прям | Без цикла | - | в m-файле | |
| Y(t)= 5t3+2t2-2t+1 | [-5;5] n=30 | Прав. Прям | for | номер итерации | через m-функцию | |
| Y(t)=sin2(4t)+1 | [0;p/6] n=30 | Ср. прям | While | аргумент | в m-файле | |
| Y(t)= sin3(4t)+1 | [0;p/6] n=15 | Трапеции | Без цикла | - | через m-функцию | |
| Y(t)=sin(6t)+cos(6t) | [0;p/10] n=20 | Симпсона | for | аргумент | в m-файле | |
| Y(t)=cos(2t)-cos(4t)-cos(6t) | [p/10; p/4] n=25 | Лев. Прям | While | номер итерации | через m-функцию | |
| Y(t)=arctg(5t)-cos(t) | [p/10;2p] n=15 | Прав. Прям | Без цикла | - | в m-файле | |
| Y(t)=t3+t+1 | [0;3] n=60 | Ср. прям | for | аргумент | через m-функцию | |
| Y(t)=cos(2t2)+1 | [-p/4; p/5] n=30 | Трапеции | While | номер итерации | в m-файле | |
| Y(t)=exp(-0.4t)+sin(t) | [0; p] n=15 | Симпсона | Без цикла | - | через m-функцию |
Задание 2
Построить график сложной функции
| № | Функция | Интервал | Тип цикла | Параметры |
| Y(t)=sin2(t)-1, t<-p/2 Y(t)=sin(4t)+1, -p/2£t£p/2 Y(t)=sin(t)-1, t>p/2 | [-p;p] шаг 0.1 | While | Желтый, сплошная | |
| Y(t)=sin(t)+sin(3t)+sin(5t), t<-p/7 Y(t)=sin(t)-sin(3t)-sin(4t), -p/7£t£3p/7 Y(t)=sin(t)+sin(2t)+sin(4t), t>3p/7 | [-p; p] шаг 0.05 | Без цикла | Розовый, пунктирная | |
| Y(t)=5-5exp(-0.1t), t<20 Y(t)=exp(-0.1t), 20£t£35 Y(t)=10-10exp(-0.05t), t>35 | [0;50] шаг 0.5 | for | Голубой, штрих-пунктирная | |
| Y(t)=sin(2t)+cos(2t), t<-p/2 Y(t)=sin(2t)-cos(2t), -p/2£t£p/2 Y(t)=sin(t)-cos(t), t>p/2 | [-p;p] шаг 0.1 | While | Красный, штриховая | |
| Y(t)=sin(3t)+sin(5t)+sin(7t), t<p/7 Y(t)=sin(3t)-sin(5t)-sin(7t), p/7£t£3p/7 Y(t)=sin(2t)+sin(4t)+sin(6t), t>3p/7 | [0; p] шаг 0.05 | Без цикла | Зеленый, сплошная | |
| Y(t)=arctg(2t)+sin(t), t<-p/2 Y(t)=arctg(2t)-sin(t), -p/2£t£p/2 Y(t)=arctg(t)+sin(2t), t>p/2 | [-p;p] шаг 0.1 | for | Синий, пунктирная | |
| Y(t)=3t2-t+1, t<-3 Y(t)=t2-2t+1, -3£t£3 Y(t)=2t2-2t+1, t>3 | [-5;5] шаг 0.1 | While | Черный, штрих-пунктирная | |
| Y(t)=sin2(4t)-1, t<-p/2 Y(t)=sin(4t)-1, -p/2£t£p/2 Y(t)=sin(2t)+1, t>p/2 | [-p;p] шаг 0.1 | Без цикла | Розовый, штриховая | |
| Y(t)=exp(-0.1t), t<3 Y(t)=5-5exp(-0.01t), 3£t£6 Y(t)=exp(-0.05t), t>6 | [0;10] шаг 0.1 | for | Красный, сплошная | |
| Y(t)=sin(6t)-cos(6t), t<-p/4 Y(t)=sin(6t)+cos(6t), -p/4£t£p/4 Y(t)=sin(t)+cos(t), t>p/4 | [-p/2;p/2] шаг 0.1 | While | Голубой, пунктирная | |
| Y(t)=10-10exp(-0.2t), t<10 Y(t)=exp(-0.2t), 10£t£20 Y(t)=exp(-0.05t), t>20 | [0;30] шаг 0.5 | Без цикла | Зеленый, штрих-пунктирная | |
| Y(t)=sin(2t)+cos(2t), t<-p/2 Y(t)=sin(2t)-cos(2t), -p/2£t£p/2 Y(t)=sin(t)-cos(t), t>p/2 | [-p;p] шаг 0.1 | for | Черный, штриховая | |
| Y(t)=4t2+4t+1, t<-4 Y(t)=4t2+4t-10, -4£t£4 Y(t)=t3+t+1, t>4 | [-7;8] шаг 0.1 | While | Розовый, штрих-пунктирная | |
| Y(t)=cos(2t2)-1, t<-p/4 Y(t)=cos(2t2)+1, -p/4£t£p/4 Y(t)=sin(2t)-1, t>p/4 | [-p;p] шаг p/20 | Без цикла | Зеленый, штриховая | |
| Y(t)=10-10exp(-0.4t), t<20 Y(t)=exp(-0.4t), 20£t£30 Y(t)=4-4exp(-0.1t), t>30 | [0;50] шаг 0.5 | While | Красная, пунктирная |