Дифференцирование комплексных функций
Понятие производной комплексной функции
Условия Коши-Римана
Аналитические и гармонические функции
Восстановление аналитической функции
Понятие производной комплексной функции
Пусть однозначная функция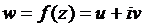 
определена в некоторой окрестности 
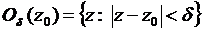точки z0. Рассмотрим всевозможные приращения
независимого переменного z, не выводящие за пределы этой окрестности. Каждому такому приращению соответствует приращение функции
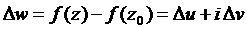
Производная функции комплексного переменного определяется как предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю:
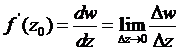(1)
Как и в случае функции действительного переменного, функцию, имеющую производную в некоторой точке, будем называть дифференцируемой в этой точке.
Представим приращение функции в виде суммы линейной части относительно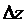 
и бесконечно малой высшего порядка по сравнению с :
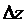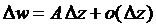
Очевидно, что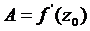 
. Главную линейную часть 
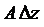этого приращения называют дифференциалом функции 
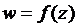в точке z0 и обозначают 
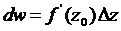. Легко проверить, что 
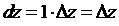. Следовательно,
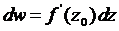(2)
Требование дифференцируемости функции комплексного переменного более жесткое, чем аналогичное требование для функции действительного переменного. Например, функция
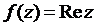
не имеет производной ни в одной точке. В самом деле, если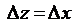 
, то 
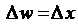и
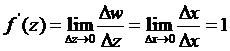
Если же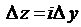 
, то 
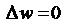и
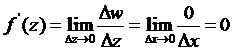
В силу свойства единственности предела функции этим доказано, что предел данной функции не существует ни в одной точке плоскости С.
Из этого примера видно, что между действительной и мнимой частями дифференцируемой комплексной функции существует некая зависимость. Такая зависимость выражается известными условиями Коши-Римана.
Условия Коши-Римана
Теорема. Пусть функция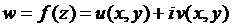 
определена в окрестности точки 
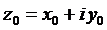. Для того чтобы она была дифференцируемой в этой точке необходимо и достаточно, чтобы действительная и мнимая части функции были дифференцируемы в этой точке и выполнялись условия Коши-Римана:
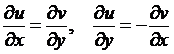(3)
Однозначная дифференцируемая в каждой точке некоторой области комплексная функция называется аналитической функцией в этой области. Таким образом, из теоремы вытекает, что функция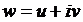 
является аналитической тогда и только тогда, когда функци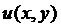и 
и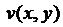 
дифференцируемы в каждой точке области и выполняются условия Коши-Римана
В условиях этой теоремы производную в декартовой системе координат можно вычислить по одной из следующих формул:
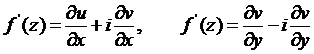(4)
Пусть функция задана в полярной системе координат: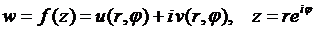 
. Тогда условия Коши-Римана принимают следующий вид:
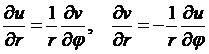(5)
Производную в полярной системе координат можно вычислить по одной из следующих формул:
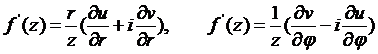(6)
Из определения производной вытекает, что правила дифференцирования суммы, разности, произведения, частного, а также сложной функции, остаются в силе.
Найдем производную функции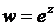 
. Действительная и мнимая части этой функции имеют непрерывные производные в любой точке комплексной плоскости С. В самом деле, из представления
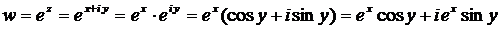
следует, что
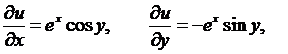
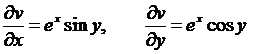
Итак, условия Коши-Римана выполнены, значит, функция 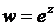дифференцируема в любой точке комплексной плоскости С. По формуле (4) получаем
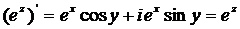
Как и в случае функции действительного переменного
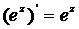
Все другие рассмотренные выше основные элементарные функции также дифференцируемы в своей области определения, причем имеют место следующие формулы:
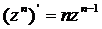
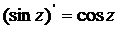
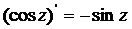
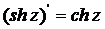
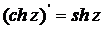
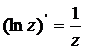
Аналитические и гармонические функции
Из условий Коши-Римана вытекает, что действительная и мнимая части аналитической функции 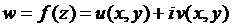удовлетворяют уравнению Лапласа:
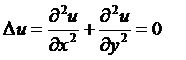
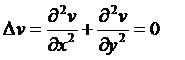
Это означает, что эти функции являются гармоническими в заданной области. Гармонические функции, удовлетворяющие условиям Коши-Римана, называются гармонически-сопряженными. Они определяют аналитическую функцию, причем, если известна одна из них, то другая определяется с точностью до константы