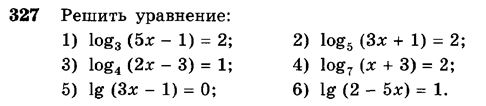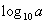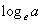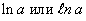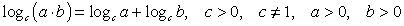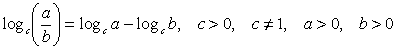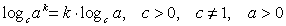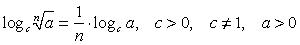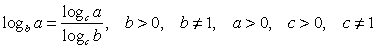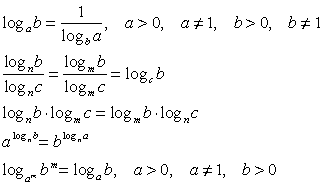План.
Понятие логарифмического уравнения.
Методы решения логарифмических уравнений.
Понятие логарифмического уравнения.
Логарифмические уравнения – уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма.
При решении логарифмических уравнений часто используются теоретические сведения:
Определение логарифма Логарифмом числа b по основаниюа называется показатель степени, в которую нужно возвести а, чтобы получить b.
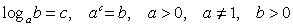
Свойства логарифма
Действия с логарифмами
| ||||||||||||||||||||
Простейшим логарифмическимуравнением служит уравнение вида
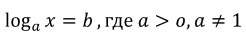
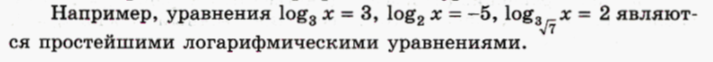
| ||||||||||||||||||||
| 2. Методы решения логарифмических уравнений. Обычно решение логарифмических уравнений начинается с определения ОДЗ. В логарифмических уравнениях рекомендуется все логарифмы преобразовать так, чтобы их основания были равны. Затем уравнения либо выражают через один какой – либо логарифм, который обозначается новой переменной, либо уравнение преобразовывают к виду, удобному для потенцирования. Преобразования логарифмических выражений не должны приводить к сужению ОДЗ, если же примененный метод решения сужает ОДЗ, выпуская из рассмотрения отдельные числа, то эти числа в конце задачи необходимо проверить подстановкой в исходное уравнение, т.к. при сужении ОДЗ возможна потеря корней. |
• По определению логарифма;
• Метод потенцирования (освобождения от знака логарифма);
• Решение уравнений с использованием свойств логарифмов;
• Метод введения новой переменной;
• Логарифмирование уравнений;
• Другие методы (функционально-графический, метод приведения к одному основанию).
Рассмотрим каждый метод более подробно.
1) ПО ОПРЕДЕЛЕНИЮ ЛОГАРИФМА.
По определению логарифма решаются простейшие уравнения вида 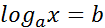 .
.
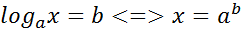 .
.
Так как логарифмическая функция возрастает (или убывает) на множестве положительных чисел и принимает все действительные значения, то по теореме о корне следует, что для любого b данное уравнение имеет, и притом только одно, решение, причем положительное.
Пример 1. Решить уравнение 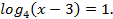
Решение: 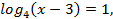
ОДЗ: 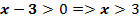 ,
,
Используем определение логарифма:
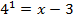 ,
,
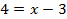 ,
,
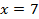 .
.
Ответ: 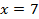 .
.
Пример 2. Решить уравнение 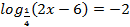 ,
,
Решение: 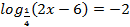 ,
,
ОДЗ: 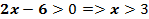 .
.
По определению логарифма:
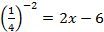 ,
,
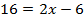 ,
,
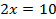 ,
,
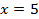 .
.
Ответ: 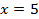 .
.
Пример 3. Решить логарифмическое уравнение:

2) МЕТОД ПОТЕНЦИРОВАНИЯ (ОСВОБОЖДЕНИЯ ОТ ЗНАКА ЛОГАРИФМА).
Решение логарифмического уравнения 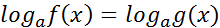 основано на том, что данное уравнение равносильно уравнению
основано на том, что данное уравнение равносильно уравнению 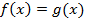 при дополнительных условиях
при дополнительных условиях
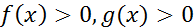 .
.

Этот способ решения называется потенцированием – переход от равенства, содержащего логарифмы, к равенству, не содержащему их.
Пример 4. Решить уравнение 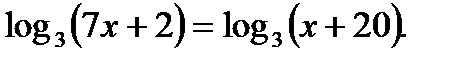
Решение:
ОДЗ: 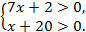 <
< 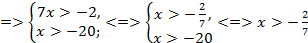 .
.
Потенцируя получим:
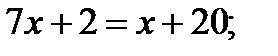
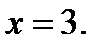
Ответ: 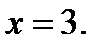
Вернемся к нашей задаче и дорешаем её. (Ответ: 6,25)
Пример 5. Решить уравнение:

3) РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ЛОГАРИФМОВ.
Пример 6. Решить уравнение
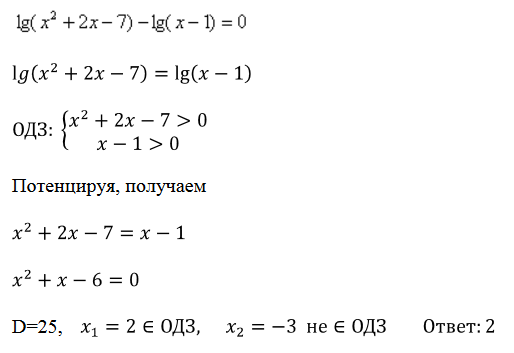
Пример 7. Решить уравнение 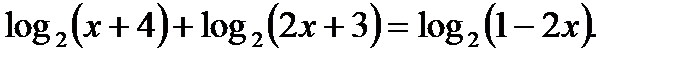
Решение:
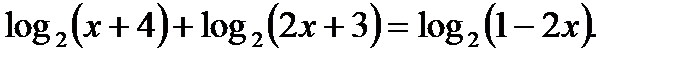
ОДЗ: 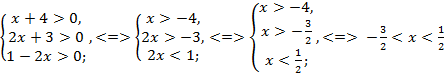 .
.
Вспомним свойства логарифмов – сумма логарифмов двух положительных чисел равна логарифму произведения этих чисел, поэтому: 
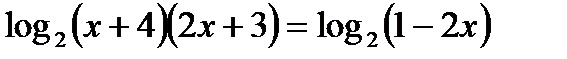
Освободимся от знака логарифма и решим квадратное уравнение:
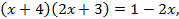
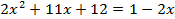 ,
,
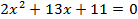 ,
,
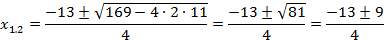
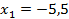 ,
, 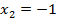 .
.
Согласовав корни с ОДЗ, получим корень 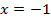 .
.
Ответ: 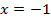 .
.
Пример 8. Решите уравнение

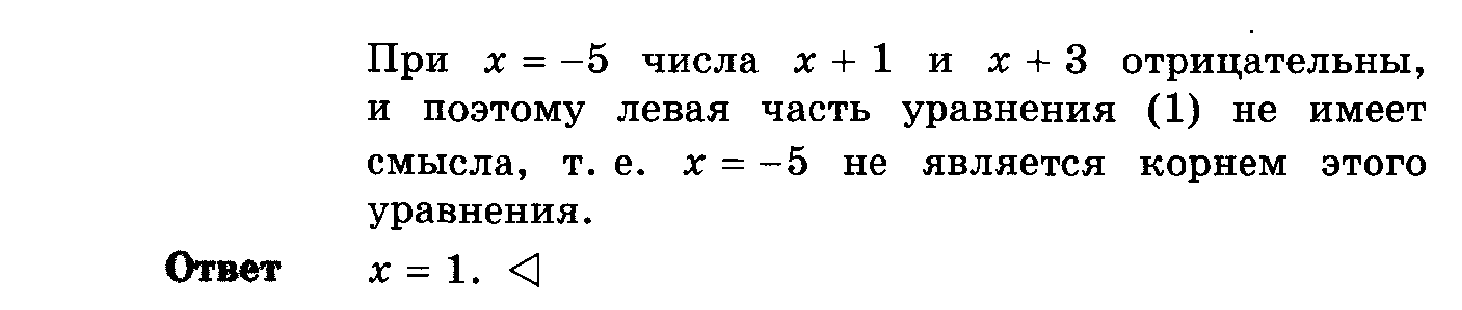
Пример 9. Решите уравнение

Пример 10. Решите уравнение
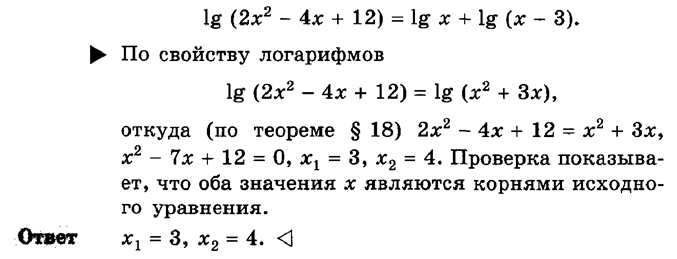
Пример 11. Решите уравнение
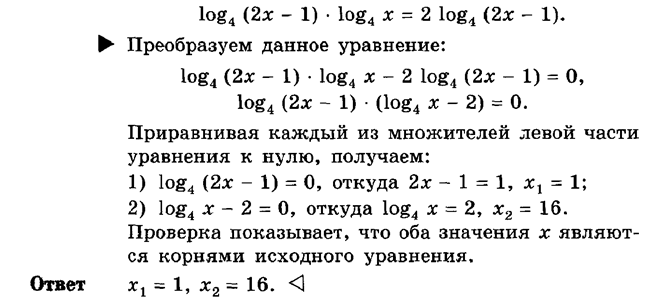
4) МЕТОД ВВЕДЕНИЯ НОВОЙ ПЕРЕМЕННОЙ.
Пример 12. Решить уравнение 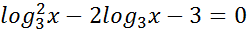
Решение:
ОДЗ: 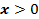
В данном уравнении повторяется выражение: 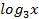 .
.
Значит можно выполнить замену переменной.
Пусть 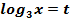 . Тогда уравнение примет вид
. Тогда уравнение примет вид 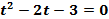
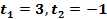
Возвратимся к исходной переменной.
Остается решить простейшие логарифмические уравнения:

Ответ: 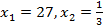 .
.
Пример 13. Решить уравнение 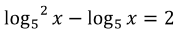

Пример 14. Решить уравнение
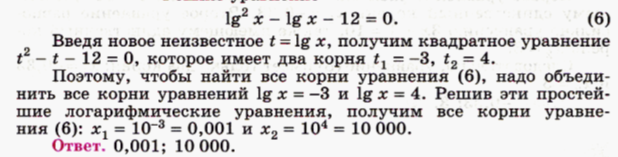
5) Рассмотрим следующий МЕТОД РЕШЕНИЯ – ФУНКЦИОНАЛЬНО-ГРАФИЧЕСКИЙ

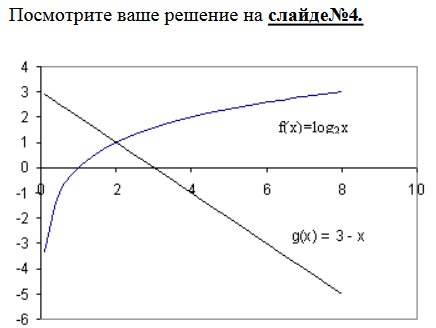
Пример 15. Решите графически 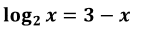
Строим по точкам графики двух функций 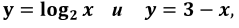 ищем абсциссу точек пересечения графиков.
ищем абсциссу точек пересечения графиков.
6) МЕТОД ПРИВЕДЕНИЕ К ОДНОМУ ОСНОВАНИЮ.
Пример 16. 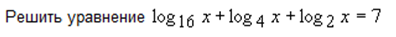
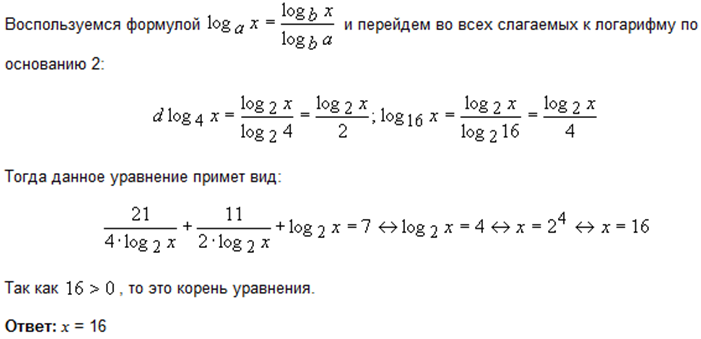
Пример 17. Решить уравнение 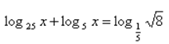
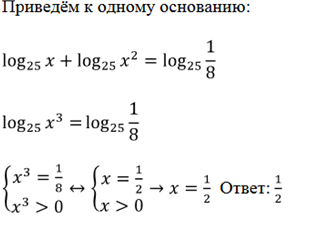
7) МЕТОД ЛОГАРИФМИРОВАНИЯ.
Этот метод применятся при решении уравнений, содержащих переменную и в основании, и в показателе степени. Если при этом в показателе степени содержится логарифм, то обе части уравнения надо прологарифмировать по основанию этого логарифма.
Пример 18. Решить уравнение:

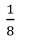 Проверка: подставив в исходное уравнение (сделать самостоятельно), получим, что оба корня подходят. Ответ: 2;
Проверка: подставив в исходное уравнение (сделать самостоятельно), получим, что оба корня подходят. Ответ: 2;
Решить уравнение.
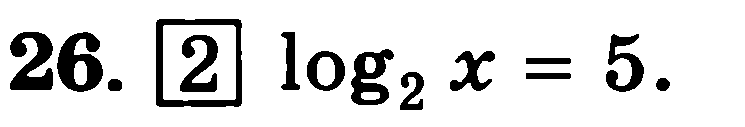
| 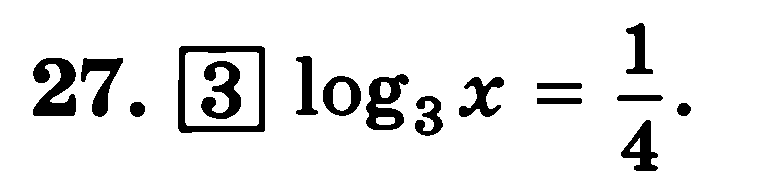
|
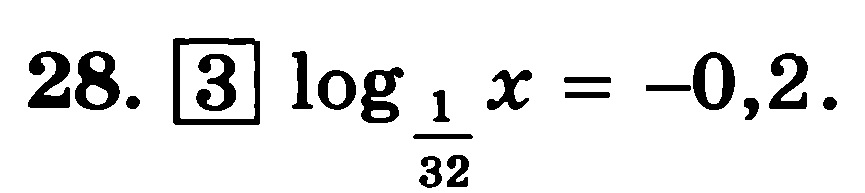
| 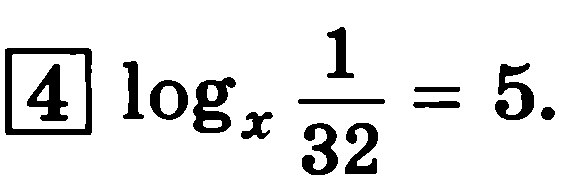
|
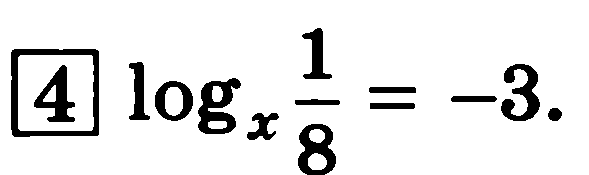
| 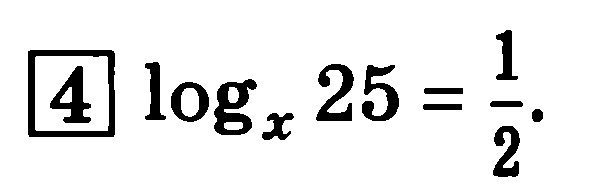
|
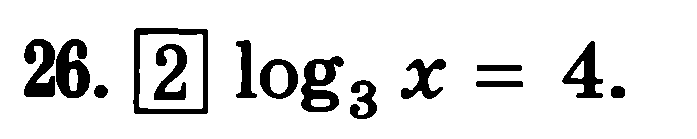
| 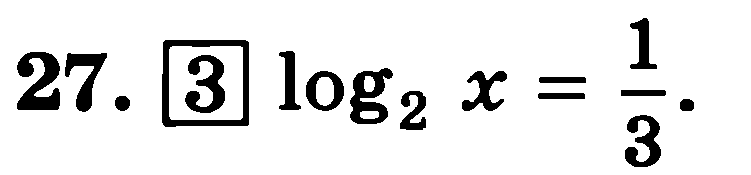
|
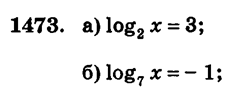
| 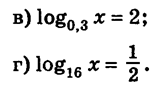
|
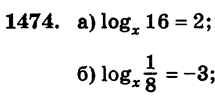
| 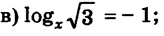
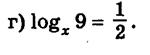
|

| 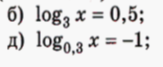 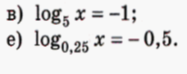
|