1. АЗ: [11], №№ 5.1, 5.5, 5.9, 5.17, 5.21, 5.23, 5.25, 5.27, 5.37, 5.41, 5.53, 5.61, 5.63, 5.69, 5.81, 5.83, 5.85, 5.94, 5.144, 5.146, 5.148, 5.164, 5.168, 5.170, 5.172, 5.184, 5.186, 5.192, 5.197, 5.290, 5.296, 5.303, 5.312.
2. Образцы решения задач
2.1 Найти 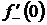 и
и 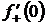 для функции
для функции 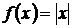
Решение: Имеем по определению
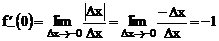


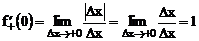
Заметим, что функция 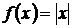 не имеет производной в точке
не имеет производной в точке 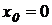
2.2 Найти производную функции 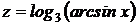 .
.
Решение: Полагая 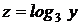 и
и 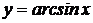 , имеем
, имеем 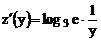 и
и 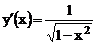 . Отсюда получаем
. Отсюда получаем 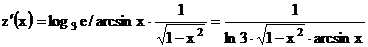 .
.
2.3 Найти 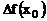 , если
, если 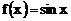 ,
, 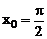
Решение:Имеем
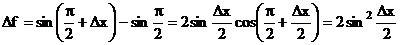 .
.
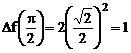
2.4 Пользуясь определением производной функции, найти производную функции 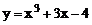 в точке
в точке 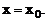
Решение. Дадим значению 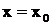 приращение
приращение 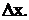 Тогда функция
Тогда функция 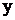 получит приращение:
получит приращение:
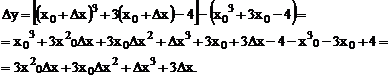
Найдем:
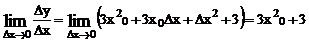
Итак, 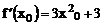 .
.
2.5 Составить уравнения касательной и нормали к кривой 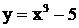 в точке (2,3).
в точке (2,3).
Решение  Напишем уравнение пучка прямых, проходящих через данную точку (2,3)
Напишем уравнение пучка прямых, проходящих через данную точку (2,3) 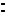
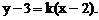
Вычислим: 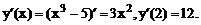
Тогда, для касательной: 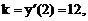 для нормали
для нормали 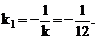
Подставляя эти значения в уравнение пучка прямых, получим 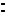
уравнение касательной 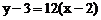 или
или 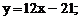
уравнение нормали 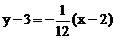 или
или 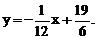
2.6 Найти производную: 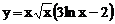
Решение.Преобразуем функцию 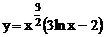 .
.
Тогда
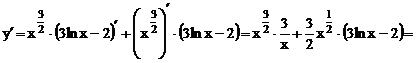
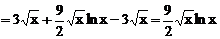 .
.
2.7 Найти 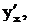 если
если 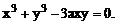
Решение. 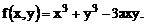 Вычислим:
Вычислим: 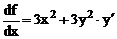
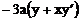
Тогда 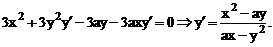
2.8 Найти 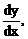 если
если 
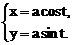
Решение.Находим 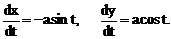 Тогда
Тогда
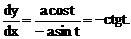
2.9 Найти вторую производную функции, заданной параметрическим уравнением: 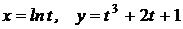 .
. 

Решение: В соответствии с формулами имеем:
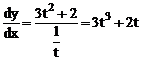
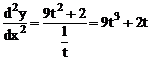
3. ДЗ: [11], №№ 5.2, 5.10, 5.11, 5.22, 5.26, 5.38, 5.54, 5.62, 5.70, 5.82, 5.86, 5.95, 5.145, 5.147, 5.165, 5.169, 5.171, 5.185, 5.193, 5.198, 5.291, 5.304, 5.305, 5.313.
Практ. зан № 9 Тема 8 Производные и дифференциалы высших порядков. Теоремы о среднем для дифференцируемых функций. Формула и ряд Тейлора.
1. АЗ: [11], №№ 5.316, 5.322, 5.329, 5.331, 5.337, 5.339, 5.346, 5.349, 5.364, 5.380, 5.382, 5.394.
2. Образцы решения задач
2.1 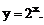 Найти
Найти 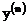
Решение.
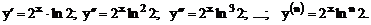
2.2 Найти 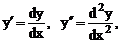 если
если 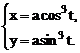
Решение. 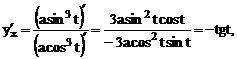
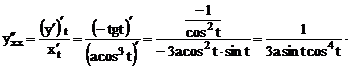
Сравнить приращение и дифференциал функции
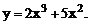
Решение. Найдем 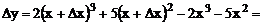
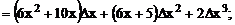
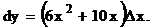
Разность между приращением 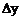 и дифференциалом
и дифференциалом 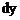 есть бесконечно малая высшего порядка по сравнению с
есть бесконечно малая высшего порядка по сравнению с 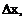 равная
равная
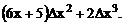
2.4 Вычислить приближенное значение 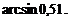
Решение.Полагаем 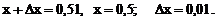
Применим формулу
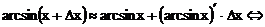
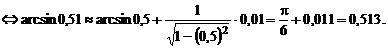
2.5 Найти дифференциал второго порядка функции 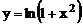 .
.
Решение: Имеем 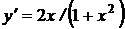 ,
, 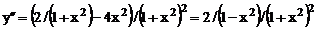 . Тогда
. Тогда 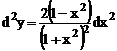 .
.
2.6 Найти 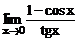 .
.
Решение. Имеем 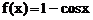 ,
, 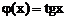 ,
, 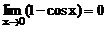 ,
,
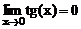 . Производные
. Производные 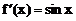 и
и 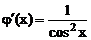 существуют и конечны в окрестности точки
существуют и конечны в окрестности точки 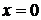 , причем
, причем 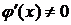 . Выполнены условия правила Лопиталя, применяя его, получим:
. Выполнены условия правила Лопиталя, применяя его, получим: 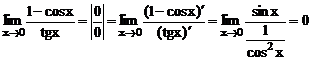 .
.
2.7 Найти 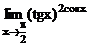 .
.
Решение.Это неопределенность вида 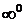 . Положим
. Положим 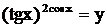 .
.
Тогда 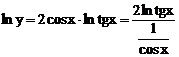 .
.
Рассмотрим
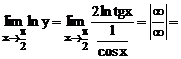
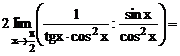
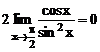 .
.
Следовательно, 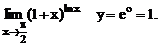
3. ДЗ: [11], №№ 5.317, 5.323, 5.332, 5.338, 5.347, 5.365, 5.381, 5.383, 5.395.
Практ. зан. № 10. Тема 9 Раскрытие неопределенностей. Исследование поведения функций и их графиков. Приложения дифференциального исчисления к геометрии.
1. АЗ: [11], №№ 5.404, 5.413, 5.415, 5.440, 5.442, 5.452, 5.453, 5.461, 5.463.
[14], №№ АЗ- 6.10
2. Образцы решения задач
2.1 Найти интервалы возрастания и убывания функции 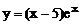 . Исследовать функцию на экстремум.
. Исследовать функцию на экстремум.
Решение.Найдем производную 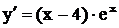 и стационарные точки, решая уравнения
и стационарные точки, решая уравнения 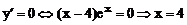 . Определим знак производной
. Определим знак производной 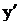 в окрестности точки
в окрестности точки 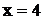 :
: 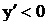 при
при 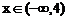 и
и 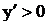 при
при 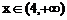 . Следовательно, в точке
. Следовательно, в точке 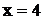 функция имеет минимум
функция имеет минимум 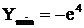 . Функция возрастает на интервале
. Функция возрастает на интервале 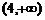 ; убывает на интервале
; убывает на интервале 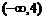 .
.
2.2 Исследовать на экстремум функцию 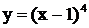 . Найти интервалы возрастания и убывания.
. Найти интервалы возрастания и убывания.
Решение.Вычислим 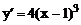 . Найдем стационарную точку
. Найдем стационарную точку 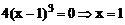 .
.
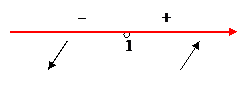
Функция убывает при 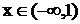 ; возрастает при
; возрастает при 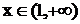 .
.
2.3 Найти наибольшее и наименьшее значения функции 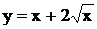 на отрезке
на отрезке 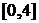 .
.
Решение.Найдем производную:
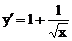 .
.
Критическая точка 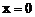 . Вычислим значения функции:
. Вычислим значения функции:
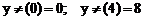 .
.
Итак, наименьшее значение функции равно 0, а наибольшее равно 8.
2.4 Найти точки перегиба кривой 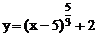 .
.
Решение. Находим 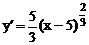 ,
, 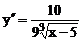 . Критическая точка второго рода:
. Критическая точка второго рода: 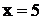 .
.
Определим знак 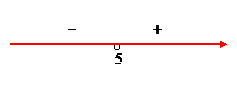
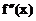 в окрестности
в окрестности 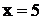 .
.
Следовательно, точка 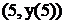 , т.е. (5,2) – точка перегиба.
, т.е. (5,2) – точка перегиба.
2.5 Найти асимптоты кривой 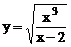 .
.
Решение.Функция определена в интервалах 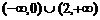 . Имеем
. Имеем 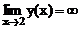 , следовательно
, следовательно 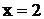 - вертикальная асимптота. Горизонтальных асимптот нет, так как предел
- вертикальная асимптота. Горизонтальных асимптот нет, так как предел 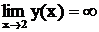 не является конечной величиной. Находим:
не является конечной величиной. Находим:
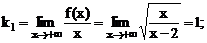
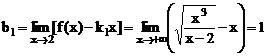 .
.
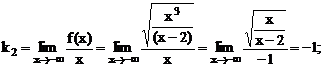
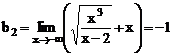 .
.
Итак, наклонные асимптоты: 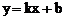 , т.е.
, т.е. 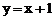 и
и  .
.
2.6 Исследовать и построить график функции 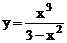
Решение.
1) 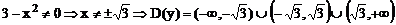
2) 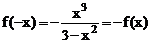 , т.е. функции нечетная.
, т.е. функции нечетная.
Поэтому график функции симметричен относительно начала координат. Следовательно, исследования проведем для 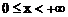 .
.
Затем воспользуемся симметрией.
3) 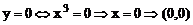 - точка пересечения с осями координат.
- точка пересечения с осями координат.
4) Найдем 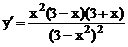 .
.
Решим уравнение 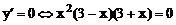
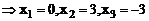 . Исследуем только точку
. Исследуем только точку 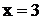 . Определим знак производной в окрестности этой точки.
. Определим знак производной в окрестности этой точки.
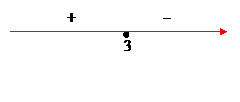
Следовательно, 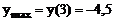 ; функция возрастает при
; функция возрастает при 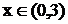 и убывает при
и убывает при 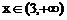 .
.
5). Вычислим:
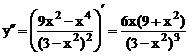 .
.
Тогда 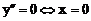 . Определим знак
. Определим знак 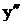 в окрестности точке
в окрестности точке 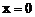 и
и 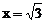
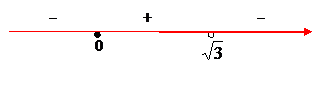
Следовательно 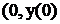 ), т.е.
), т.е. 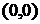 – точка перегиба; кривая вогнута при
– точка перегиба; кривая вогнута при 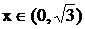 и выпукла при
и выпукла при 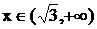 .
.
6) Имеем 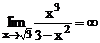 , следовательно,
, следовательно, 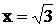 - вертикальная асимптота.
- вертикальная асимптота.
Вычислим:
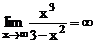 , т.е. горизонтальных асимптот нет.
, т.е. горизонтальных асимптот нет.
Найдем:
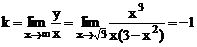 ,
,
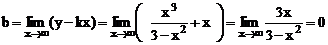 .
.
Итак, 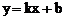 , т.е.
, т.е. 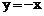 наклонная асимптота.
наклонная асимптота.
7). Вычислим:
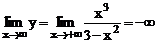 ;
;
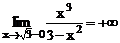 ;
; 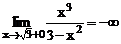 .
.
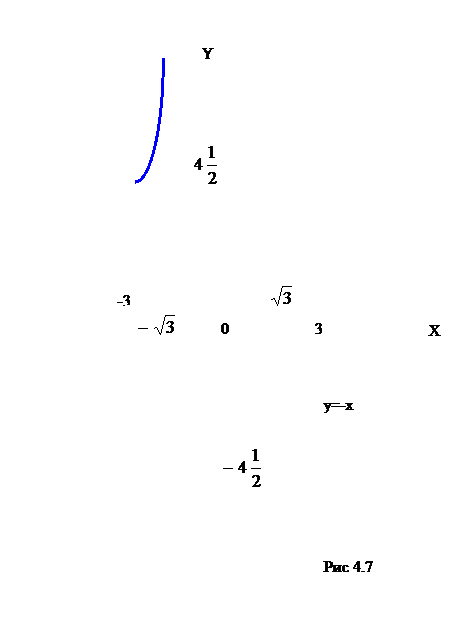
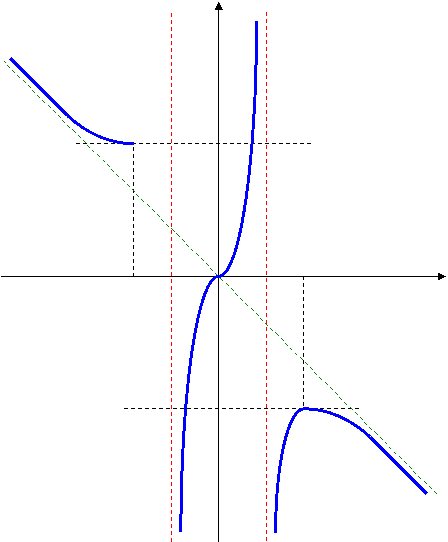 Построим график функции
Построим график функции
3. ДЗ: [11], №№ 5.405, 5.406, 5.412, 5.414, 5.441, 5.454, 5.462.
[14], СР, стр. 204-205.