Пусть на интервале 
задана дифференцируемая функция 
. Геометрически это означает, что в каждой точке график функции имеет касательную. Наклон касательной зависит от знака производной в точке касания. Если производная больше нуля, то угол наклона касательной острый (рис.1а) и наоборот, если производная меньше нуля, то угол наклона касательной тупой (рис.1б).
рис.1а. рис.1б.
Теорема 2. Пусть функция 
определена и непрерывна на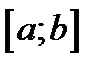 
, дифференцируема
на 
и если:
1) 
2) 
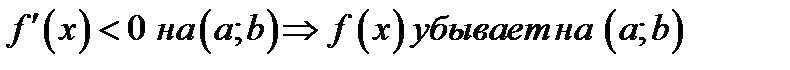
Доказательство. Докажем 1). Как всегда берём любую пару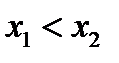 
из 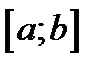. Нужно доказать, что 
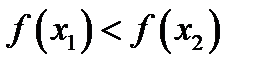. На сегменте 
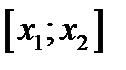выполнены все условия теоремы Лагранжа (проверьте!). Запишем формулу Лагранжа для этого случая
(1)
Так как
.
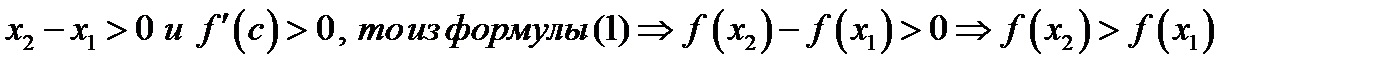Теорема доказана. Доказательство пункта 2) предоставляем читателю.
Приведём алгоритм определения экстремальных точек (используются только первые производные).
Правило 1 отыскания локальных экстремумов дифференцируемой функции 
:
1. Найти стационарные точки, в которых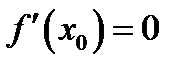 
.
2. Из найденных точек 
оставляем те, при переходе через которые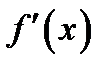 
меняет знак.
3. Локальный максимум достигается в точках , при переходе через которые 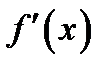меняет знак с положительного на отрицательный.
4. Локальный минимум достигается в точках , при переходе через которые 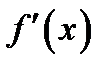меняет знак с отрицательного на положительный.
5. Замечание. Экстремума нет в тех точках, при переходе через которые 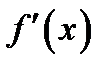не меняет знак.
Определение 4. Функция, дифференцируемая на интервале
, выпукла вверх, если её производная на этом интервале убывает.
Определение 4. Функция, дифференцируемая на интервале , выпукла вниз, если её производная на этом интервале
возрастает.
Теорема 3. Пусть функция 
дважды дифференцируема на интервале 
тогда, если 
Доказательство. Докажем пункт 1) теоремы. По условию,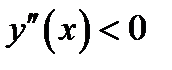 
следовательно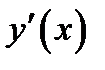 
убывает. Из определения 3 следует, что функция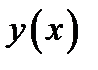 
выпукла вверх.
Докажем пункт 2) теоремы. По условию, 
следовательно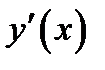
возрастает. Из определения 4 следует, что функция 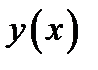выпукла вниз.
Замечание. Как известно, из двух точек с одинаковыми абсциссами 
и 
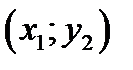выше
лежит точка, у которой ордината больше и наоборот ниже лежит точка, у которой
ордината меньше.
Теорема 4. Точки графика выпуклой вверх дифференцируемой функции 
лежат нижелюбой касательной проведённой к графику.
Доказательство. Пусть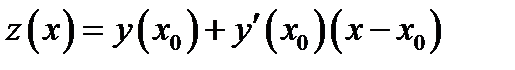 
уравнение касательной прямой, проведённой к графику функции в точке касания 
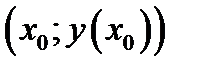. Докажем, что любая точка касательной лежит выше точки графика функции (см. замечание выше), то есть 
для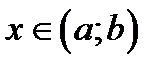 
. Примем для определённости, что точка 
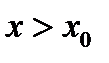.Рассмотрим разность
Применяя теорему Лагранжа о среднем к разности 
, получаем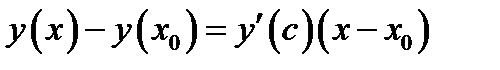 
. Отсюда 
, 
.
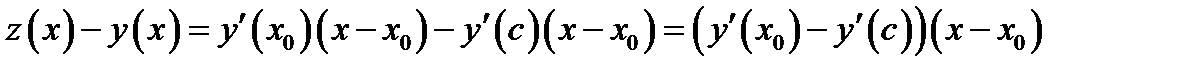По условию у нас производная 
функции убывает. Следовательно, разность
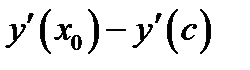положительна. Отсюда следует, что 
и поэтому точка 
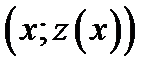
лежит выше точки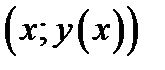 
. Теорема доказана. Аналогично рассматривается случай, когда
точка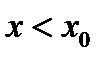 
.
Теорема 5. Точки графика выпуклой вниз функции лежат вышелюбой касательной проведённой к графику.
Доказательство аналогично доказательству теоремы 4.
Точки, при переходе через которые, график функции меняет выпуклость на противоположную
называются точками перегиба графика функции.
Определение 6. Точка 
, лежащая на графике функции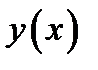 
, будет точкой перегиба графика функции, если
1) график функции 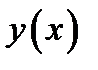имеет в точке касательную прямую;
2) слева и справа от точки выпуклости графика противоположно направлены.