Разложение по формуле Маклорена основных элементарных функций.
1) 




(30)Достаточные условия сущ. экстремума. 1)  существует в точке
существует в точке  , и равна 0 называется стационарной. Экстремумы функции возможны где производная существует и равна нулю
, и равна 0 называется стационарной. Экстремумы функции возможны где производная существует и равна нулю
(т. Ферма), а также формы где не существует причем  всегда внутренняя точка. 2)
всегда внутренняя точка. 2)  , т.е. при переходе через точку
, т.е. при переходе через точку  слева направо производная меняет знак с - на + тогда
слева направо производная меняет знак с - на + тогда  имеет локальный минимум 3) Если
имеет локальный минимум 3) Если  на всей окрестности, то есть при переходе через точку
на всей окрестности, то есть при переходе через точку  , производная не меняет знак, то в точке
, производная не меняет знак, то в точке  экстремума нет.
экстремума нет.
(31)Выпуклость ф- и, точки перегиба: определения и геометрический смысл. 1) Точка  - точка перегиба кривой
- точка перегиба кривой  , если при переходе x через точку кривой
, если при переходе x через точку кривой  переходит с одной стороны наклонной на другую. 2) Функция
переходит с одной стороны наклонной на другую. 2) Функция  непрерывна на некотором промежутке (a,b) называется выпуклой книзу(кверху), если для любых точек
непрерывна на некотором промежутке (a,b) называется выпуклой книзу(кверху), если для любых точек  выполняется неравенство
выполняется неравенство  для
для 
 . Для любых
. Для любых  и таких, что их сумма равна 1 3)Точка
и таких, что их сумма равна 1 3)Точка 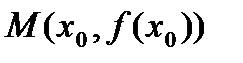 - точка перегиба кривой, если она отделяет участок на котором функция выпукла книзу(кверху) от участка где она выпукла кверху(книзу).
- точка перегиба кривой, если она отделяет участок на котором функция выпукла книзу(кверху) от участка где она выпукла кверху(книзу).
(32)Асимптоты графика функции. 1) Прямая x=a называется асимптотой графика функции  если хотя бы один из пределов
если хотя бы один из пределов 
2) Пусть  определена для любых
определена для любых  , тогда
, тогда  называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции  при
при  , если
, если  представляется в виде
представляется в виде  где
где  при
при  .
.
(33)Схема исследования функции.
1)Найти область определения и область значений
2)Приравнять  и найти т. Пересечения с Ox
и найти т. Пересечения с Ox
3)Исследовать на четность, нечетность, периодичность.
4)Исследовать на границах области определения 
5)Исследовать на непрерывность, найти точки разрыва, пределы слева и справа и определить классификацию точек разрыва.
6)Найти производную  , найти стационарные точки и точки где производная не существует. Найти точки экстремума и локальные экстремумы и указать промежутки монотонности.
, найти стационарные точки и точки где производная не существует. Найти точки экстремума и локальные экстремумы и указать промежутки монотонности.
7) 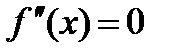 . Определить промежутки выпуклости вверх, вниз и точки перегиба.
. Определить промежутки выпуклости вверх, вниз и точки перегиба.
8)Найти асимптоты.
(34) Неопред. инт. опред. и св-ва.
Определение. Совокупность всех первообразных функции f(x) называется неопределенным интегралом от f(x) и обозначается  . f(x) называется подынтегральной функцией, а f(x)dx - подынтегральным выражением. Таким образом, окончательно
. f(x) называется подынтегральной функцией, а f(x)dx - подынтегральным выражением. Таким образом, окончательно  .
.
.
Свойства неопределенного интеграла.
1.  ;
;
2.  ;
;
3.  ;
;
4.  .
.
(35) Таблица интегралов

(36) Интегрирование по частям

(38)Определённый интеграл. Пусть f(x) определена на [a;b]. Разобьём [a;b] на части с несколькими произвольными точками  Тогда говорят, что произведено разбиение R отрезка [a;b]. Определённым интегралом от функции f(x) на отрезке [a;b] назыв. предел интегральных сумм при стремлении ранга разбиения к нулю
Тогда говорят, что произведено разбиение R отрезка [a;b]. Определённым интегралом от функции f(x) на отрезке [a;b] назыв. предел интегральных сумм при стремлении ранга разбиения к нулю
Если существует указанный предел, то функция f(x) называется интегрируемой на [a;b].
Св-ва:
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы.
, где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю. 
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный. 
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам. 
V. Постоянный множитель можно выносить за знак определенного интеграла. 
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций. 
(39) Теорема о среднем
Пусть f(x) непрерывна на [a;b] тогда сущ.  такая что
такая что 
(40) Геом. приложения опред. интеграла(S,V, l)
 ;
;  ;
; 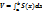
(41) Несобств. инт. 1 рода, опред. и св-ва.
Пусть f(x) опред. (a;∞) и сущ.  при любом А>a. Обозначим
при любом А>a. Обозначим 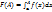 , тогда, если сущ.
, тогда, если сущ.  , конечный предел, то он назыв. несобств. инт. 1 рода
, конечный предел, то он назыв. несобств. инт. 1 рода  . В противн. случае, если не сущ. конечного пред., то инт. назыв. расходящимся, если сущ. – сходящимся.
. В противн. случае, если не сущ. конечного пред., то инт. назыв. расходящимся, если сущ. – сходящимся.
(42) Несобств. инт. 2 рода, опред. и св-ва.
Пусть f(x) интергрир. на (a;A), при любом A>a, f(x) неогранич. в лев. полуокрестн. точки b. 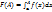 , если сущ.
, если сущ.  , то он назыв. несобств. инт. 2 рода
, то он назыв. несобств. инт. 2 рода 
(43) Исслед. несоб. инт. на сходимость.
Очень часто нужно узнать сходится интеграл или расходится, не вычисляя его. Для этого используются признаки сходимости, которые мы сформулируем сразу для несобственных интегралов обоих типов, полагая, что b может быть бесконечным или конечной особой точкой. Признаки сходимости: Если интеграл 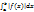 сходится, то интеграл
сходится, то интеграл  тоже сходится. В этом случае интеграл
тоже сходится. В этом случае интеграл  называют абсолютно сходящимся. Пусть
называют абсолютно сходящимся. Пусть  . Тогда, если интеграл
. Тогда, если интеграл  сходится, то интеграл
сходится, то интеграл  тоже сходится и, если интеграл
тоже сходится и, если интеграл  расходится, то интеграл
расходится, то интеграл  тоже расходится. 3. Пусть b есть особая точка функции f (x). Если при x → b существует предел
тоже расходится. 3. Пусть b есть особая точка функции f (x). Если при x → b существует предел  то интегралы
то интегралы  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
1) 
2) (хn)=n•хn-1
3) (ex)'=ex
4) (aх)'=aхInа
5) 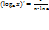
6) (sinx)'=cosx.
7) (cosх)'=-sinx
8) 
9) 
10) 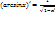
11) 
12) 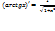
13) 

1) 
2) (хn)=n•хn-1
3) (ex)'=ex
4) (aх)'=aхInа
5) 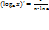
6) (sinx)'=cosx.
7) (cosх)'=-sinx
8) 
9) 
10) 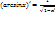
11) 
12) 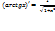
13) 
