ТОЧНОСТЬ И КАЧЕСТВО ИСПЫТАНИЙ ПРИ СТАТИСТИЧЕСКОМ МОДЕЛИРОВАНИИ
План лекции
1. Общая схема фиксации и обработки результатов моделирования.
2. Статистическая обработка независимых реализаций критерия интерпретации.
3. Оценка точности и необходимого количества реализаций модели.
4. Использование правил автоматической остановки
Общая схема фиксации и обработки результатов моделирования
Модель сложной системы в качестве одного из основных элементов включает в себя набор показателей, характеризующих свойства системы: качество функционирования, надежность, качество управления и т.д.
Целью моделирования является оценка этих показателей. На основе этих оценок выбирается наилучший вариант проектируемой системы или обосновываются рекомендации по улучшению существующей системы.
Процедура получения этих оценок в общем случае выглядит следующим образом. Имитируется процесс функционирования системы на определенном промежутке времени [0,Т]. В процессе работы моделирующего алгоритма вычисляется и запоминается ряд величин, характеризующих этот процесс: У(t)=[У1(t),У2(t),...,Уn(t)], (0<=t<=T)
В самом общем случае Уi(t) представляют собой случайные функции времени.
По значениям этих величин и требуется сделать выводы качестве системы, т.е. требуется дать интерпретацию результатов моделирования. Это делается при помощи расчетов специальных величин - критериев интерпретации.
Количественный показатель, рассчитываемый по результатам моделирования, по которому судят о свойствах исследуемой системы, называют критерием интерпретации 
.
Он должен быть достаточно простым. Обычно это среднее значение какой-либо случайной величины или вероятность какого-либо события.
Поскольку вектор результатов У(t) - случайный вектор, то находят путем статистической обработки значений У(t). Это в значительной мере определяет схему построения вычислительного алгоритма.
Предположим для определенности, что алгоритм, моделирующий функционирование системы на промежутке [0,T] построен по принципу 
t, т.е. состояние системы фиксируется в моменты времени, равные 0, t,2 t,..., k t=T
Для каждого момента вычисляется значение Y(j t), j=0,1..k. Работу модели на промежутке [0,T] обычно называют прогоном.
Для обеспечения статистической устойчивости значений критерия интерпретации производят несколько прогонов модели до получения требуемой точности. Для определенности будем полагать, что производится N прогонов. Допустим также, что конечной целью моделирования является сравнение нескольких вариантов построения системы.
Тогда общая схема моделирующего алгоритма примет вид (рис.10.1):
В конкретных случаях эта схема может быть упрощена.
Рис.10.1. Общая схема обработки результатов моделирования
Статистическая обработка независимых реализаций критерия интерпретации
Пусть по результатам моделирования оценивается критерий 
. Будем считать, что - какая-то характеристика случайной величины У. (Например, =P{У>0} или =М[У]).
Рассмотрим некоторые понятия математической статистики. В результате моделирования мы получаем N значений У: У1, У2,...,Уn. В статистике говорят о выборке объема N. Если повторить эксперимент, то выборка получится другой. Поэтому в математической статистике называют выборкой систему из N независимых случайных величин У1, У2,...,Уn, имеющих одно и то же распределение, совпадающее с распределением У.
Выборка используется для получения оценок тех или иных характеристик У. Например, вычисляется оценка для математического ожидания:
В правой части этого равенства стоит величина, полностью определяемая выборкой.
Всякая функция от выборки называется оценкой (или статистикой). Пусть неизвестная характеристика распределения У, которую требуется оценить. Процесс выглядит следующим образом. По выборке оценивается
и принимается за приближенное значение 
. Поскольку 
оказывается случайной величиной, то о качестве приближения судят по различным характеристикам.
Оценка называется несмещенной, если М[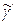 
]= . О близости можно судить по величине D[ 
]=М[( - )*( 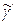- )]. Оценку с наименьшей при данном N дисперсией называют эффективной. Отметим еще свойство состоятельности. Оценку называют состоятельной, если для каждого
Для состоятельных оценок можно говорить о доверительном интервале. Зададим уровнем доверительной вероятности 1-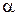 
,где 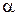=0.05, 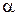=0,001...), и точностью ε. Найдем по определению состоятельности такое N, чтобы
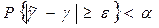
Тогда с вероятностью 1- 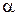(близкой к единице) не выйдет за доверительные границы ( - 
< 
< 
+ 
)
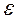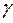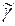Таким образом, в принципе с любой точностью можно оценить неизвестное значение . Это можно сделать с любой степенью надежности.
Особенно удобно построение доверительных оценок для асимптотически нормальных оценок.
Оценку называют асимптотически нормальной, если ее распределение стремится к нормальному при N--> 
:
Рассмотрим доверительный интервал для асимптотически нормальной оценки. Пусть задача доверительная вероятность 1- 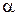. Найдем 
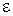такое, что 
Можно записать это соотношение в виде
и оценить значение этой вероятности как
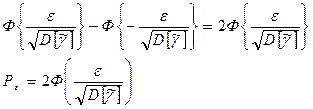
Приравнивая правую часть к 1- 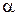, получим
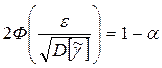или 
Решение уравнения Ф(ta) = (1- 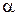)/2 обозначается ta - квантиль нормального распределения. Для него составляются таблицы. Ким образом,
, откуда 
Следовательно, для асимптотически нормальной оценки с вероятностью не более чем 1- 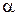справедливо неравенство
Это неравенство и служит мерой достигнутой точности вычисления