Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 равна длине данного отрезка PQ, причем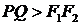 
.
Точки F1 и F2 называют фокусами эллипса, а расстояние между ними – фокальным расстоянием. Прямая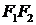 
называется фокальной осью.
Обозначим длину данного отрезка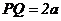 
, а фокальное расстояние 
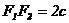(по определению с>а). Обозначим
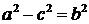. (1)
Введем в рассмотрение специально выбранную прямоугольную декартову систему координат, в которой фокусы F 1и F 2 расположены на оси абсцисс симметрично относительно начала координат.Тогда фокусы имеют координаты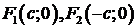 
. Пусть точка 
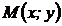принадлежит эллипсу, тогда из определения эллипса имеем
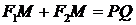(2)
или
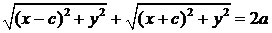(3)
Возведем в квадрат равенство (3)
,
,
,
.
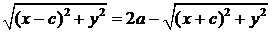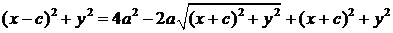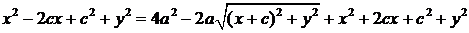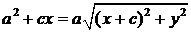Последнее равенство снова возведем в квадрат:
.
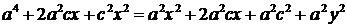Выполним группировку
.
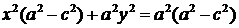С учетом (1) имеем:
.
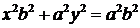Разделив равенство на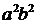 
получим
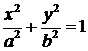. (4)
Таким образом, если точка принадлежит эллипсу, то ее координаты удовлетворяют уравнению (4). Покажем, что имеет место и обратное утверждение: если координаты точки удовлетворяют уравнению (4), то точка лежит на эллипсе, т.е.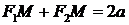 
. Из уравнения (3) выразим 
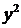и найдем фокальные радиусы точки М.
,
,
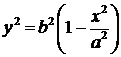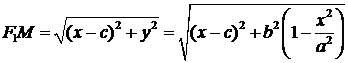Т.к. имеет место (1), то
.
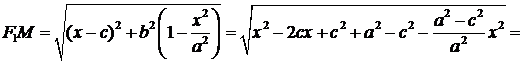
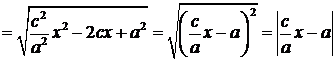Аналогично,
.
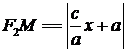Из равенства (1) следует, что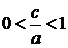 
, а из (3) имеем, что 
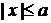, значит, 
, 
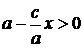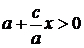, поэтому
, 
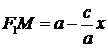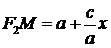. (5)
Поэтому, 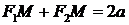, т.е. точка М принадлежит эллипсу.
Уравнение (4) называют каноническим уравнением эллипса, выбранная система координат называется канонической.
Отрезк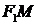и 
и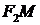 
называют фокальными радиусами точки М.
Из уравнения (3) вытекает ряд свойств эллипса:
1. Координаты точки О (0; 0 ) не удовлетворяют уравнению эллипса (4), следовательно, эллипс не проходит через начало координат.
2. Переменные х и у входят в уравнение эллипса в четных степенях. Значит, если точка с координатами (х0,у0) принадлежит эллипсу, то и точки с координатами (- х0; у0), (х0; - у0), (- х0; - у0) также удовлетворяют уравнению эллипса. Это означает, что эллипс симметричен относительно осей координат и начала координат.
3. Эллипс пересекает каждую из осей координат в двух точках.Ось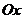 
- в точках 
, ось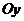 
- 
.
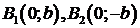Точки А 1 ,А 2 ,В 1 ,В 2 называют вершинами эллипса, а отрезки А 1 А 2и В 1 В 2– осями эллипса: А 1 А 2 =2а, В 1 В 2 =2b, т.к. а>b, то А 1 А 2 – большая ось, В 1 В 2– малая. Числа а и b называют полуосями эллипса.
4. Из уравнения (4) следует, что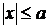 
, 
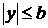или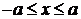 
, 
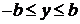. Это означает, что все точки эллипса принадлежат прямоугольнику, ограниченному прямыми 
, 
.
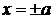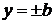5. В силу симметрии эллипса относительно осей координат и начала координат представление о его строении можно получить, рассмотрев точки первой координатной четверти. Для точки 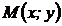первой четверти (
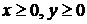) имеем: 
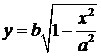. При возрастании х от 0 до а ордината y точки М убывает от b до 0.
6. Рассмотрим прямую l проходящую через начало координат. Зададим ее параметрическими уравнениями
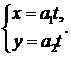
Найдем точки пересечения прямой с эллипсом. Для этого подставим x, y в уравнение (4):
.
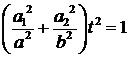Откуда находим
.
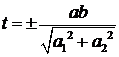Следовательно, любая прямая, проходящая через центр эллипса пересекает его в двух точках.
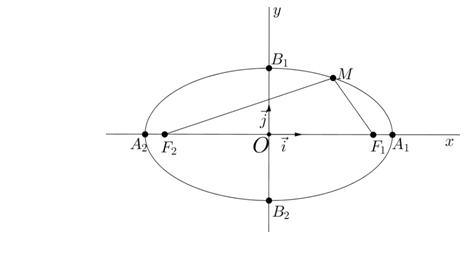
Рис. 31
Эксцентриситетом эллипса называется число, равное отношению фокального расстояния к большей оси
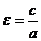. (6)
Так как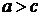 
, то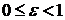 
. Вычислим отношение 
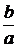через эксцентриситет:
.
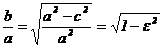Отсюда следует, что среди эллипсов, имеющих одну и ту же большую полуось, но разные эксцентриситеты, более «продолговатым» является тот, у которого эксцентриситет больше.
Замечание. Окружность является частным случаем эллипса, для которого фокусы F 1 и F 2 совпадают. В этом случае с=0, значит, а=b, каноническое уравнение приводится к виду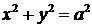 
. Эксцентриситет окружности равен 0.
Пусть эллипс g задан каноническим уравнением (4). Рассмотрим окружност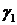и 
и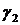 
, диаметрами которых служат большая и малая оси эллипса: 
, 
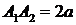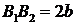. Произвольный луч, выходящий из центра О эллипса, пересечет окружност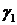и и 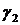в точках 
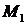и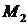 
. Проведем через точку 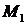прямую 
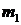, параллельную оси Оy: 
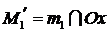. Через точку 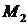прямую 
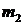, параллельную оси Ох: 
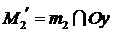. Рассмотрим множество g¢ точек М плоскости, образующееся при пересечении прямых 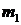и :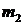 
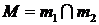. Пусть (х; y) – координаты точки М, 
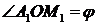. Точк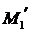и 
и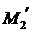 
являются проекциями точки М на координатные оси, т.е. 
, 
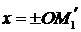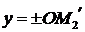. Тогда
 |
, 
.
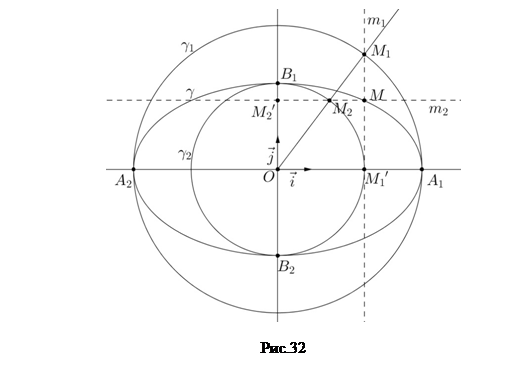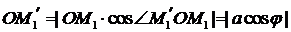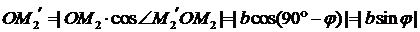Следовательно,
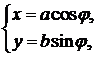(7)
где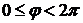 
. Из формул (5) по основному тригонометрическому тождеству имеем:
.
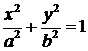Таким образом, если точка М Îg¢, то она принадлежит и эллипсу g.
Несложно убедиться и в справедливости обратного утверждения (доказать самостоятельно). Поэтому уравнения (7) называются параметрическими уравнениями эллипса.
Описанный выше способ позволяет строить любую точку эллипса, зная его полуоси.