Лекция 12. Монотонные дифференцированные функции
План
Правило Лопиталя
Критерий постоянства функции
Критерий монотонности дифференцированной функции
Достаточное условие строгой монотонности функции
Формула Тейлора
Правило Лопиталя
Пусть функции  и
и 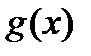 определены и дифференцированы на
определены и дифференцированы на 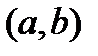 ,
, 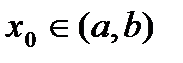 ,
, 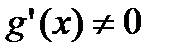 . Пусть
. Пусть
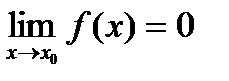 и
и 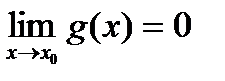 ,
,
или
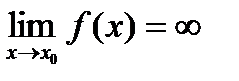 и
и 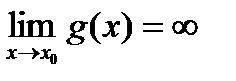 ,
,
т.е. для 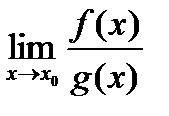 имеем неопределенность типа
имеем неопределенность типа 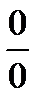 или
или 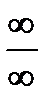 , но при этом существует
, но при этом существует
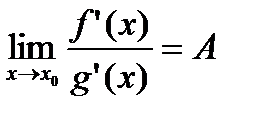 ,
,
тогда существует 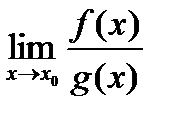 и
и
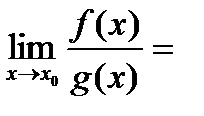
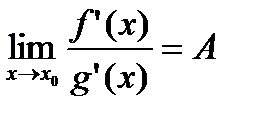 .
.
Пример. Вычислить 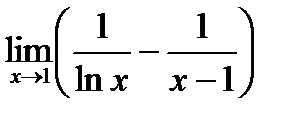 . В этом примере неопределенность типа
. В этом примере неопределенность типа 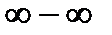 , то есть применять правило Лопиталя здесь сразу нельзя, но если выполнить вычитание, то получим:
, то есть применять правило Лопиталя здесь сразу нельзя, но если выполнить вычитание, то получим:
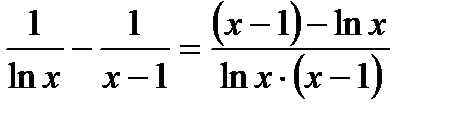 ,
,
и
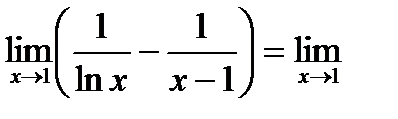
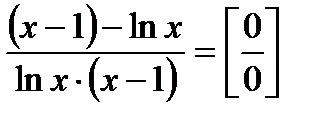 .
.
Теперь можно попробовать применить правило Лопиталя. Обозначим функцию в числителе
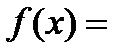
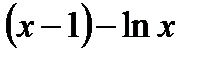 ,
,
функцию в знаменателе
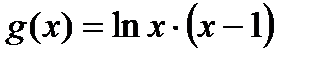 .
.
Тогда
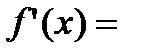
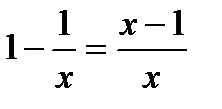 ,
, 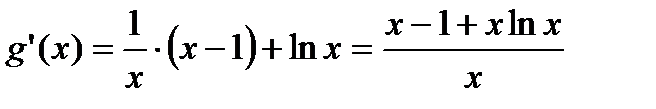 ,
,
а
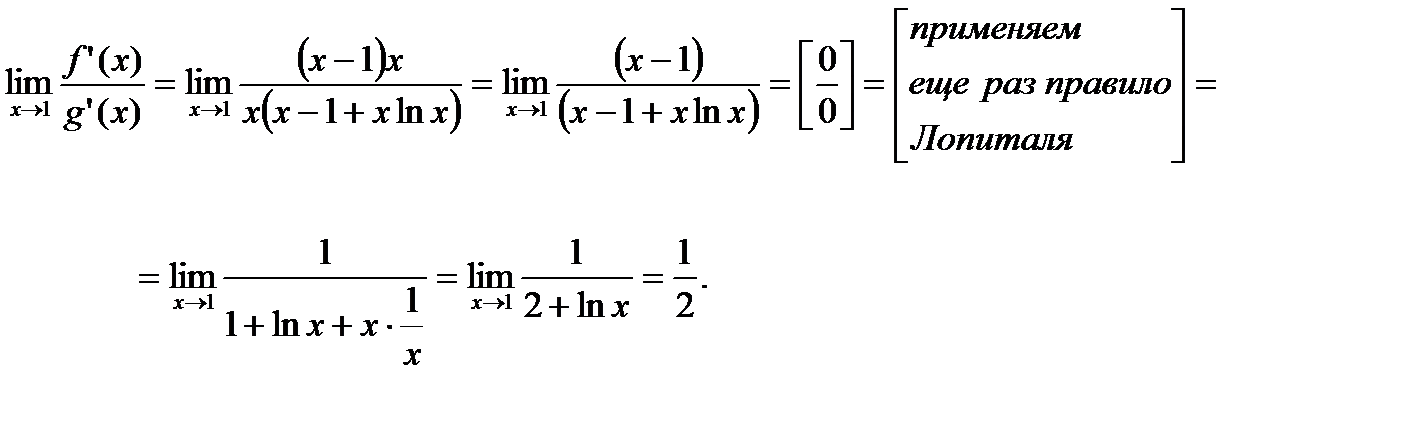
Поскольку существует 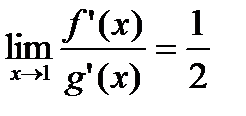 , то по правилу Лопиталя существует и рассматриваемый предел
, то по правилу Лопиталя существует и рассматриваемый предел
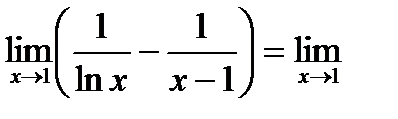
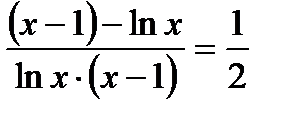 .
.
Критерий постоянства функции
Функция 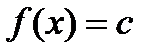 , где
, где  , называется постоянной функцией. Для постоянной функции, которая определена на некотором множестве
, называется постоянной функцией. Для постоянной функции, которая определена на некотором множестве 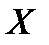 выполняется условие: для
выполняется условие: для 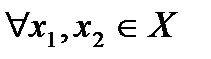 :
: 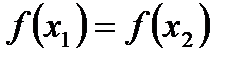 .
.
Теорема 1 (необходимое и достаточное условие постоянства функции). Пусть функция  определена и дифференцирована на
определена и дифференцирована на 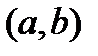 . Для того, чтобы
. Для того, чтобы  была постоянной на этом интервале необходимо и достаточно, чтобы
была постоянной на этом интервале необходимо и достаточно, чтобы
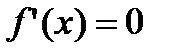 для
для 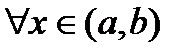 .
.
Доказательство. Необходимость. Пусть 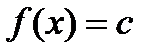 , где
, где  , тогда по правилам вычисления производных:
, тогда по правилам вычисления производных:
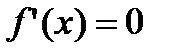 для
для 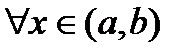 .
.
Достаточность. Пусть 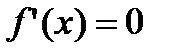 для
для 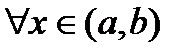 . Покажем, что тогда
. Покажем, что тогда 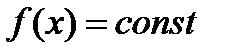 , т.е. что для
, т.е. что для 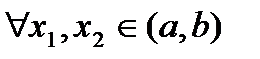 :
: 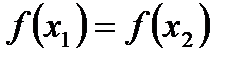 . Если рассмотреть функцию
. Если рассмотреть функцию  на
на 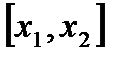 , то на этом сегменте
, то на этом сегменте  удовлетворяет всем условиям теоремы Лагранжа, поэтому для нее имеет место формула Лагранжа:
удовлетворяет всем условиям теоремы Лагранжа, поэтому для нее имеет место формула Лагранжа:
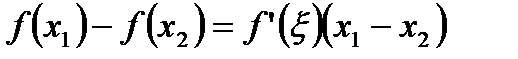 , де
, де 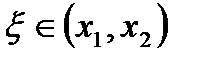 .
.
Поскольку 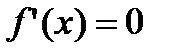 для
для 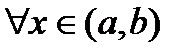 , то
, то 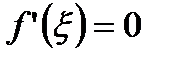 , а потому
, а потому
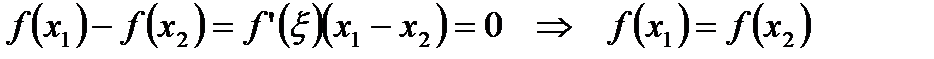 .
.
Критерий монотонности дифференцированной функции
Определение 1. Пусть функция  определена на
определена на 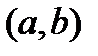 . Эта функция называется монотонно возрастающей (убывающей) на
. Эта функция называется монотонно возрастающей (убывающей) на 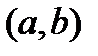 , если для
, если для 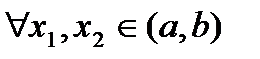 из того, что
из того, что 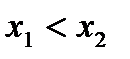 вытекает, что
вытекает, что 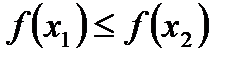 (
( ).Функция будет строго монотонно возрастающей (строго убывающей) на
).Функция будет строго монотонно возрастающей (строго убывающей) на 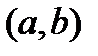 , если для
, если для 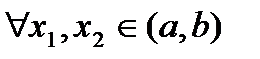 из того, що
из того, що 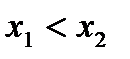 вытекает, что
вытекает, что 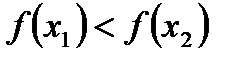 (
(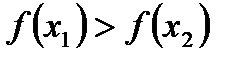 ).
).
Пример. Функция 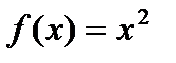 строго монотонно возрастает на множестве
строго монотонно возрастает на множестве 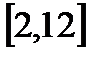 , строго монотонно убывает на множестве
, строго монотонно убывает на множестве 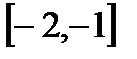 .
.
Теорема 2 (необходимое и достаточное условие монотонности функции). Пусть функция  определена и дифференцирована на
определена и дифференцирована на 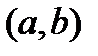 . Для того, чтобы
. Для того, чтобы  монотонно возрастала (убывала) на этом интервале необходимо и достаточно, чтобы
монотонно возрастала (убывала) на этом интервале необходимо и достаточно, чтобы
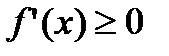 (
(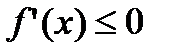 ) для
) для 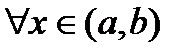 .
.
Доказательство. Докажем теорему для случая монотонного возрастания функции.
Необходимость. Пусть  монотонно возрастает на
монотонно возрастает на 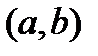 . Покажем, что
. Покажем, что 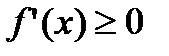 для
для 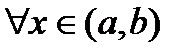 . Возьмем
. Возьмем 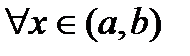 . Для вычисления производной построим разностное отношение для
. Для вычисления производной построим разностное отношение для  в точке
в точке 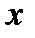 и вспомним, что поскольку
и вспомним, что поскольку 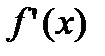 существует в
существует в 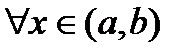 по условию теоремы, то
по условию теоремы, то 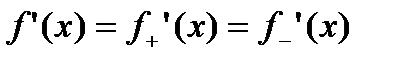 . Учитывая это:
. Учитывая это:
 ,
,
что и нужно было доказать.
Достаточность. Пусть 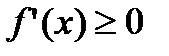 для
для 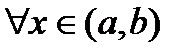 . Покажем, что
. Покажем, что  монотонно возрастает на
монотонно возрастает на 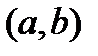 . Возьмем произвольно
. Возьмем произвольно 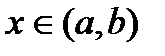 и
и 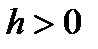 так, что
так, что 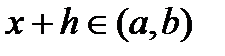 . Рассмотрим функцию
. Рассмотрим функцию  на сегменте
на сегменте 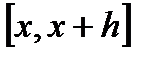 . На этом сегменте она удовлетворяет всем условиям теоремы Лагранжа, поэтому
. На этом сегменте она удовлетворяет всем условиям теоремы Лагранжа, поэтому 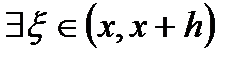 , что
, что
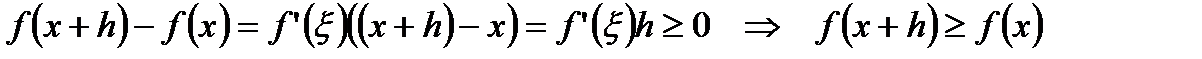 ,
,
что говорит о монотонном возрастании функции на 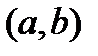 .
.
Замечание. Если функция  строго монотонно возрастает на
строго монотонно возрастает на 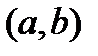 , из этого не вытекает, что
, из этого не вытекает, что 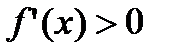 .
.
Пример. Функция 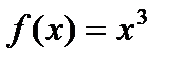 строго монотонно возрастает на всем множестве
строго монотонно возрастает на всем множестве 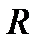 (по определению), поскольку большему значению аргумента отвечает большее значение функции, но производная
(по определению), поскольку большему значению аргумента отвечает большее значение функции, но производная 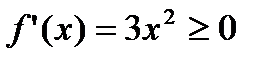 и может равняться нулю:
и может равняться нулю: 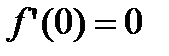 .
.