Идея дисперсионного анализа

ДИСПЕРСИОННЫЙ АНАЛИЗ

Цели работы

Целями работы являются: 1) изучение метода дисперсионного анализа с целью установления влияния факторов (входных величин) на отклик системы; 2) исследование вопросов применимости метода дисперсионного анализа для решения конкретных статистических задач.

Содержание работы

- изучить процедуру дисперсионного анализа;

- ответить на вопросы теста;

- с использованием ЭВМ решить конкретные задачи однофакторного дисперсионного анализа;

- получить результаты и составить отчет по работе.

Постановка задачи дисперсионного анализа

Во многих областях практической деятельности встречаются процессы, состояния которых зависят от входных переменных (факторов) не имеющих количественного описания. Для изучения влияния факторов на выходную функцию (отклик), их общего оценивания, ранжирования и выделения среди них существенных используется подход, получивший название дисперсионный анализ. Идея подхода заключается в изучении влияния факторов по величинам дисперсии выходной величины (отклика).

Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменчивость значений функций отклика. С этой целью производится разложение дисперсии наблюденных значений отклика на составляющие, порождаемые независимыми факторами.

Рассмотрим постановку задачи дисперсионного анализа в общем виде. Выходная переменная Y может зависеть (по физическим причинам) от n независимых факторов (x₁,x₂,…,x_n), при том факторы не всегда имеют количественное описание. Каждый фактор может варьироваться на m уровнях. Каждая строка с индексом j содержит m наблюдений выходной переменной Y.

Требуется определить, в какой мере существенно на фоне случайных погрешностей, влияние того или иного фактора x_i на отклик Y, провести сравнение с другими факторами и выделить наиболее существенные из них.

Допущения, на которых базируется дисперсионный анализ

Наблюдения переменной Y - есть нормально распределенные случайные величины с математическим ожиданием M[Y]=m_y. Дисперсия единичного наблюдения 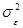обусловлена случайными ошибками ε, постоянна во всех опытах и на всех уровнях факторов x_i .

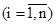Идея дисперсионного анализа

Чтобы иметь возможность оценивать влияние каждого фактора на переменную Y и сравнивать влияние различных факторов следует установить некоторый количественный показатель этого влияния. Рассмотрим идею дисперсионного анализа на примере изучения влияния одного фактора X на m уровнях, получим значения отклика y₁,y₂,…,y_n, рассеяние которых можно характеризовать выборочной дисперсией , где 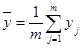. Число степеней свободы есть ν₀=m- 1. Если отличие от 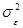незначимо, то разброс наблюдений, который она характеризует, связан только со случайными причинами и влияние фактора X несущественно. Если же отличие от 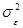значительно, то повышенный разброс наблюдений вызывается не только случайными причинами, но и влиянием фактора X, которое следует признать существенным.

Так как в последнем случае складывается влияние по крайней мере двух факторов: 1) случайных причин с дисперсией 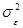; 2) фактора X с дисперсией 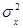, что приводит к общему рассеянию наблюдений, то их общая дисперсия является суммой 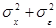, а ее оценка:

Откуда дисперсия фактора X определяется выражением:

В общем случае дисперсия ошибок 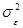неизвестна, поэтому схема дисперсионного анализа должна быть такой, чтобы позволяла определить ее наряду с оценкой дисперсии фактора X. С этой целью планируется проведение серии параллельных опытов на каждом из всех возможных сочетаний уровней факторов. Таким образом, основная идея дисперсионного анализа заключается в разложении оценки общего рассеяния на составляющие, зависящие от: 1) случайных причин; 2) от каждого из рассматриваемых факторов.

Алгоритм решения задачи

Рассмотрим процедуру однофакторного дисперсионного анализа. Пусть фактор X варьируется на n уровнях. Результаты можно представить в виде следующей таблицы:

			…	p
	y₁₁	y₁₂	…	y₁_p
	y₂₁	y₂₂	…	y₂_p
…	…	…	…	…	…
N	y_n1	y_n2	…	y_np

Не нарушая общности выводов, рассмотрим случай равночисленных серий наблюдений на всех уровнях 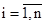, т.е p_i=p.

Рассеяние между столбцами обусловлено ошибкой воспроизводимости, а рассеяние между строчками – действием изучаемого фактора X. Вычислим среднее арифметическое 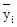серий из p наблюдений для каждого i -го уровня фактора с помощью соотношения вида:

(1)

Общее среднее арифметическое 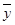всех n×p наблюдений по всем уравнениям вычисляется следующим образом:

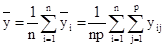(2)

Рассеяние отдельных наблюдений относительно общего среднего обусловлено действием как случайных причин, так и влиянием фактора X. Действие фактора случайности проявляется в рассеянии (с дисперсией 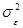) наблюдений серий параллельных исследований на каждом уровне x_i вокруг среднего арифметического своей серии. Влияние же фактора X (с дисперсией 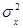) вызывает повышенное рассеяние средних арифметических относительно общего среднего 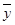. Каждое из этих трех рассеяний можно охарактеризовать соответствующей суммой квадратов отклонений. В соответствии с основной идеей дисперсионного анализа разложим общую сумму квадратов отклонений y_ij от общего среднего 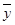на две составляющие, одна из которых характеризует влияние фактора случайности, а другая – фактора изменчивости:

(3)

Оценки дисперсий: Предположим, что влияние фактора Х на отклик отсутствует, т.е. гипотеза Н₀ об однородности , 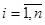верна. Тогда все n серий параллельных наблюдений можно рассматривать как случайные выборки одной и той же генеральной совокупности и, следовательно:

1) Несмещенная общая оценка дисперсии воспроизводимости по всем n×p наблюдениям определяется выражением:

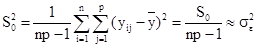(4)

с числом степеней свободы ;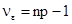

2) выборочная дисперсия рассеивания «внутри серий» или остаточная оценка дисперсии воспроизводимости 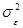, находится как среднее из выборочных дисперсии по каждой серии в отдельности:

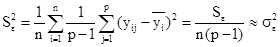(5)

с числом степеней свободы ;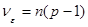

3) выборочная дисперсия средних по сериям служит несмещенной оценкой дисперсии 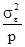с которой нормально распределены независимые друг от друга средние i- ых серий:

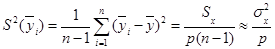(6)

с числом степеней свободы 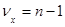. Отсюда нетрудно получить третью оценку воспроизводимости, выборочную дисперсию рассеивания «между сериями»:

(7)

с числом степеней свободы 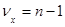. Подсчет чисел степеней свободы проверяется с помощью соотношения .

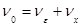Из сказанного очевидно, что при отсутствии влияния фактора Х оценки 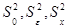однородны, так как являются оценками одной и той же генеральной дисперсии.

Предположим теперь, что влияние фактора Х на отклик существенно, т.е. гипотеза Н₀ об однородности , 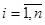неверна. Тогда n серий наблюдений можно рассматривать как случайные выборки независимых нормально распределенных случайных величин с одной и той же дисперсией воспроизводимости 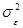и различными генеральными средними m₁,m₂,…,m_n и, следовательно:

1) выборочная дисперсия характеризует влияние как фактора случайности ε, так и фактора Х, т.е. ;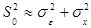

2) так как сумма 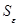не изменяется при замене y_ij на y_ij-m_i, то выборочная дисперсия также не изменяется и по-прежнему является несмещенной оценкой для генеральной дисперсии воспроизводимости 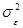, т.е. ;

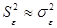3) поскольку сумма 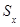учитывает не только случайные, но и систематические расхождения между средними серий и увеличивается за счет влияния фактора Х, дисперсия при этом также увеличивается и перестает служить оценкой только 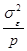, откуда следует, что .

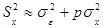Из сделанного второго предположения очевидно, что при влиянии фактора Х оценки 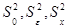неоднородны. Следовательно, сопоставляя эти выборочные дисперсии, можно принять решение о справедливости первого или второго предположения относительно существенности влияния фактора Х (с дисперсией 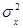) на отклик.

Оценка влияния фактора. Для того, чтобы влияние фактора Х было признано существенным (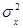 >0), необходимо и достаточно, чтобы оценка дисперсии значимо отличалось от . Проверку исходной гипотезы Н₀ об однородности этих выборочных дисперсии можно осуществить с помощью критерия Фишера:

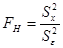(8)

При использовании критерия Фишера применяется следующее правило принятие решения: Если , то влияние фактора Х признается существенным, и, наоборот, если , то влияние фактора Х признается несущественным.

Содержание отчета

1. Описание процедуры дисперсионного анализа, с указанием соотношений (1)-(8).

2. Результаты решения каждой из трех задач в виде:

вычисленные средние по каждой серии ();

общее среднее ();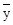

оценка дисперсии рассеивания «между сериями»;

оценка дисперсии рассеивания «внутри серии»;

значение критерия Фишера (Fn);

результат анализа: зависит или нет процесс от фактора.

Идея дисперсионного анализа

Поиск по сайту