Определение 9. Пусть дана последовательность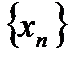 
и некоторая совокупность натуральных чисел: 
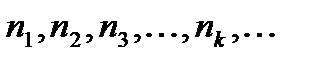, для которой
.
Последовательность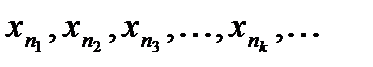 
называется подпоследовательностью 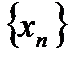и обозначается 
.
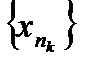Элементы подпоследовательности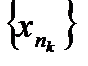 
– это подмножество элементов данной последовательности 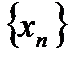, для которых сохраняется порядок. Например, пусть дана последовательность 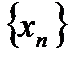, для которой 
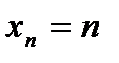, т.е. ее элементы – это
.
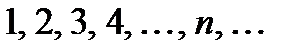Тогда подмножество элементов, которые стоят на четных местах в 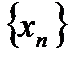, выписанных с сохранением их порядка, даст подпоследовательность :
.
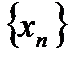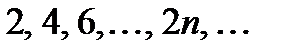Совокупность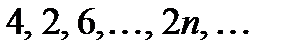 
- не является подпоследовательностью 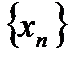, потому что здесь нарушен порядок первоначальный элементов: в последовательности 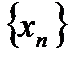сначала встречается элемент 2, а потом 4, поэтому и в подпоследовательности, которая содержит и 2, и 4, надо было сохранить такой самый порядок.
Замечание 4. Любая последовательность имеет бесконечно много подпоследовательностей. Сама последовательность является одновременно своей подпоследовательностью.
Теорема 2 (Больцано-Вейерштрасса). Из любой ограниченной последовательности 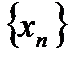можно выделить сходящуюся подпоследовательность (без доказательства).
Пример. Рассмотрим последовательность 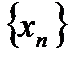, для которой 
: 
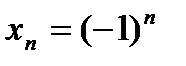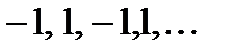. Эта последовательность является ограниченной: для 
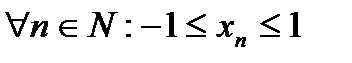. Из этой последовательности действительно можно выделить сходящуюся подпоследовательность (и не одну). Например, подпоследовательность элементов, которые имеют четные номера: 1,1,1,.... Эта подпоследовательность является сходящейся, ее предел – 1.
Замечание5. Если последовательность 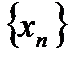имеет предел 
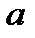, это все ее подпоследовательности имеют тот же самый предел.
Задание. Доказать замечание 5.
Утверждение 3. Если из последовательности можно выделить две подпоследовательности, которые стремятся к разным пределам, то данная последовательность является расходящейся.
Задание. Доказать утверждение 2.
Замечание6. Если из последовательности можно выделить две подпоследовательности, которые стремятся к одному пределу, то о сходимости представленной последовательности вообще ничего сказать нельзя: она может быть как сходящейся (если все другие ее подпоследовательности стремятся к тому же самому пределу), так и расходящейся (если существует какая-то другая подпоследовательность у представленной последовательности, которая стремится к другому пределу).
Теорема 3. Из любой последовательности 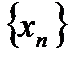обязательно можно выделить сходящуюся подпоследовательность, или бесконечно большую подпоследовательность (без доказательства).
Вопросы
1. Предел какой последовательности определяет число Эйлера?
2. Неравенство Бернулли. Доказать.
3. Где в доказательстве неравенства Бернулли использовано требование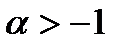 
?
4. Вывести число Эйлера.
5. Какая последовательность называется фундаментальной? Определение нефундаментальной последовательности. Привести примеры фундаментальных и нефундаментальных последовательностей.
6. Как связаны между собой фундаментальность и сходимость последовательности? Критерий Коши сходимости последовательности.
7. Какие последовательности называются бесконечно малыми, бесконечно большими? Привести примеры бесконечно малых, бесконечно больших последовательностей.
8. Какие свойства присущи бесконечно малым, бесконечно большим последовательностям?
9. Понятие подпоследовательности. Свойства подпоследовательностей.