ЛЕКЦИЯ №5. НЕКОТОРЫЕ АСПЕКТЫПОСТРОЕНИЯ МОДЕЛЕЙ
МНОЖЕСТВЕННОЙ РЕГРЕССИИ
ПЛАН
5.1. Явление мультиколлинеарности. Признаки присутствия
мультиколлинеарности в модели
Способы уменьшения (устранения) мультиколлинеарности
В модели
Применение фиктивных переменных в регрессионном анализе
Нелинейная регрессия
5.1. Явление мультиколлинеарности. Признаки присутствия
мультиколлинеарности в модели
Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. Мультиколлинеарность означает наличие линейной зависимости между факторными признаками в модели. Линейная взаимосвязь между признаками может проявляться как в функциональной, так и в статистической формах.
Если между объясняющими переменными существует линейная функциональная связь, то ранг матрицы 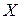 становится меньше числа оцениваемых по МНК параметров модели, т.е.
становится меньше числа оцениваемых по МНК параметров модели, т.е. 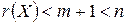 , что нарушает условие 6 теоремы Гаусса-Маркова. В этом случае матрица
, что нарушает условие 6 теоремы Гаусса-Маркова. В этом случае матрица 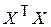 будет иметь линейно зависимые столбцы, а ее определитель станет равным нулю. Следовательно, вычисление наилучшего вектора оценок
будет иметь линейно зависимые столбцы, а ее определитель станет равным нулю. Следовательно, вычисление наилучшего вектора оценок 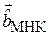 по формуле (3.5) будет невозможным. Для устранения мультиколлинеарности такого вида следует исключить из модели ту объясняющую переменную, которая связана линейной зависимостью с другими объясняющими переменными.
по формуле (3.5) будет невозможным. Для устранения мультиколлинеарности такого вида следует исключить из модели ту объясняющую переменную, которая связана линейной зависимостью с другими объясняющими переменными.
Однако чаще всего линейная связь между объясняющими переменными носит статистический характер, что проявляется в значительной коррелированности факторных признаков. В этом случае вектор МНК-оценок 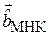 формально может быть вычислен по формуле:
формально может быть вычислен по формуле: 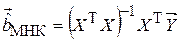 , но определитель матрицы
, но определитель матрицы 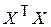 становится близок к нулю. Поскольку дисперсии оценок
становится близок к нулю. Поскольку дисперсии оценок 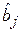
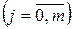 пропорциональны диагональным элементам обратной матрицы
пропорциональны диагональным элементам обратной матрицы 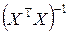 (см. формулы 4.6), то близость к нулю определителя матрицы
(см. формулы 4.6), то близость к нулю определителя матрицы 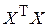 может привести к резкому увеличению дисперсий
может привести к резкому увеличению дисперсий 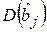 . В результате появляются следующие признаки присутствия явления мультиколлинеарности в модели: оценки
. В результате появляются следующие признаки присутствия явления мультиколлинеарности в модели: оценки 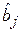
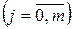 могут иметь большие стандартные ошибки, малую значимость, в то время как модель в целом остается значимой. Как следствие, МНК-оценки параметров модели становятся статистически неустойчивыми: небольшие изменения в исходных данных (например, урезание или добавление небольшой порции исходных данных) могут привести к значительному изменению значений оценок
могут иметь большие стандартные ошибки, малую значимость, в то время как модель в целом остается значимой. Как следствие, МНК-оценки параметров модели становятся статистически неустойчивыми: небольшие изменения в исходных данных (например, урезание или добавление небольшой порции исходных данных) могут привести к значительному изменению значений оценок 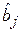
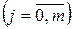 . При этом возможно как появление неверного знака у оценок
. При этом возможно как появление неверного знака у оценок 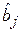 , так и появление неожиданно больших (с точки зрения экономической теории) значений
, так и появление неожиданно больших (с точки зрения экономической теории) значений 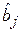
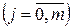 . В результате модель становится непригодной для анализа и прогнозирования.
. В результате модель становится непригодной для анализа и прогнозирования.
5.2. Способы уменьшения (устранения)
мультиколлинеарности в модели
Одним из распространенных способов уменьшения (устранения) мультиколлинеарности в модели является отбор факторов в модель на основе анализа матрицы парных коэффициентов корреляции. Для этого используют матрицу парных коэффициентов корреляции:
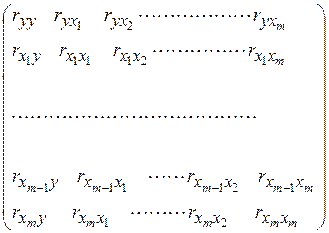
Заметим, что эта матрица является симметричной, т.к. 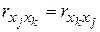 и
и 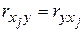 , а на главной диагонали ее стоят единицы, т.к.
, а на главной диагонали ее стоят единицы, т.к. 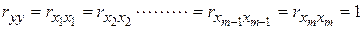 .
.
Отбор факторов в модель на основе анализа матрицы парных коэффициентов корреляции осуществляется по следующему алгоритму: в модель включают только те факторы из 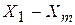 , которые наиболее сильно связаны с зависимой переменной
, которые наиболее сильно связаны с зависимой переменной 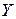 , но при этом слабо связаны с другими объясняющими переменными. При этом связь между объясняющими переменными считается сильной, если парный коэффициент корреляции между ними больше числа 0,8 по абсолютной величине.
, но при этом слабо связаны с другими объясняющими переменными. При этом связь между объясняющими переменными считается сильной, если парный коэффициент корреляции между ними больше числа 0,8 по абсолютной величине.
Другим способом устранения (уменьшения) мультиколлинеарности является пошаговый отбор в модель наиболее информативных переменных. Суть его состоит в следующем. Пусть имеются признаки мультиколлинеарности в модели, содержащей набор объясняющих переменных 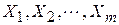 . На первом шаге в модель вводят ту объясняющую переменную из
. На первом шаге в модель вводят ту объясняющую переменную из 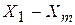 , которая имеет с зависимой переменной
, которая имеет с зависимой переменной 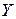 максимальный коэффициент детерминации.
максимальный коэффициент детерминации.
На втором шаге в модель включается новая объясняющая переменная, которая вместе с выбранной на первом шаге переменной составляет пару, имеющую с переменной 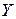 наиболее высокий коэффициент детерминации. Таким образом, на втором шаге в модель отбирают двойку наиболее информативных объясняющих переменных.
наиболее высокий коэффициент детерминации. Таким образом, на втором шаге в модель отбирают двойку наиболее информативных объясняющих переменных.
На третьем шаге в модель отбирают тройку наиболее информативных переменных, включающую в себя результаты выбора на предыдущих шагах, и т.д.
Такие действия по включению новых переменных в модель следует повторять до тех пор, пока для отобранных переменных будет увеличиваться скорректированный коэффициент детерминации. Результирующая модель будет содержать набор наиболее информативных объясняющих переменных и иметь максимальный скорректированный коэффициент детерминации.
Рассмотренные выше способы устранения мультиколлинеарности могут дать разные наборы объясняющих переменных, которые следует включить в модель. Это объясняется тем, что такие пошаговые процедуры присоединения-удаления переменных гарантируют лишь получение близкого к оптимальному набора переменных, следовательно, получаемые с помощью разных пошаговых процедур наборы переменных не обязательно совпадают.
Применение фиктивных переменных в регрессионном анализе
При проведении регрессионного анализа часто случается, что отдельные факторы, включенные в модель, являются качественными, и, следовательно, не измеряются в числовой шкале. Один из возможных подходов к решению таких задач – учет влияния качественных факторов посредством введения фиктивных переменных. В качестве фиктивных переменных чаще всего используются булевы переменные, которые принимают только два значения: “0” или “1”. Пусть, например, требуется исследовать зависимость рыночной цены квартиры 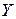 в городе Самара не только от ряда количественных факторов
в городе Самара не только от ряда количественных факторов 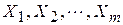 , но и от качественного фактора – месторасположения продаваемой квартиры
, но и от качественного фактора – месторасположения продаваемой квартиры 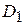 . Качественный признак
. Качественный признак 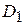 указывает на то, расположена ли квартира достаточно близко к историческому центру города, или же она находится на окраине города. Регрессионная модель цены квартиры может быть записана в виде:
указывает на то, расположена ли квартира достаточно близко к историческому центру города, или же она находится на окраине города. Регрессионная модель цены квартиры может быть записана в виде:
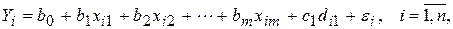
где 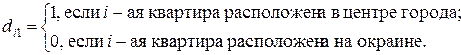
Если 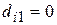 , то свободный член регрессии равен
, то свободный член регрессии равен 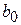 , если же
, если же 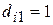 , то свободный член регрессии станет
, то свободный член регрессии станет 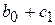 . Коэффициенты уравнения
. Коэффициенты уравнения 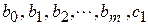 можно оценить по МНК. Если МНК-оценка
можно оценить по МНК. Если МНК-оценка 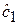 окажется статистически значимой, то можно считать, что цена за квартиру в центре города в среднем на
окажется статистически значимой, то можно считать, что цена за квартиру в центре города в среднем на 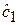 выше, чем на окраине при неизменных значениях других факторов, включенных в модель.
выше, чем на окраине при неизменных значениях других факторов, включенных в модель.
Если качественный признак имеет  уровней (т.е. количество его различных качественных состояний равно
уровней (т.е. количество его различных качественных состояний равно  ), то число булевых переменных в модели следует взять равным
), то число булевых переменных в модели следует взять равным 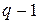 . Например, месторасположение продаваемой квартиры можно описать
. Например, месторасположение продаваемой квартиры можно описать 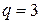 уровнями: первый уровень означает, что квартира находится в центре города; второй уровень – на окраине; третий уровень – в пригороде. В этом случае следует ввести
уровнями: первый уровень означает, что квартира находится в центре города; второй уровень – на окраине; третий уровень – в пригороде. В этом случае следует ввести 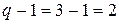 булевых переменных:
булевых переменных: 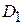 и
и 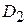 . Регрессионная модель цены квартиры примет вид:
. Регрессионная модель цены квартиры примет вид:
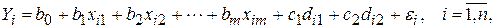
где 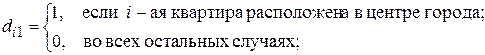
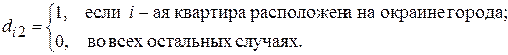
Если 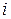 -ая квартира расположена в центре города, то это будет отражено следующей парой значений фиктивных переменных:
-ая квартира расположена в центре города, то это будет отражено следующей парой значений фиктивных переменных: 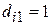 и
и 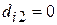 ; если же
; если же 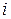 -ая квартира расположена на окраине города, то это будет отражено такой парой значений:
-ая квартира расположена на окраине города, то это будет отражено такой парой значений: 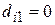 и
и 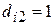 ; а если
; а если 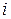 -ая квартира расположена в пригороде, то
-ая квартира расположена в пригороде, то 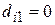 и
и 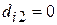 .
.
Пример 5.1. Требуется исследовать зависимость рыночной цены на квартиру 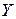 (тыс. у.е.) от общей площади
(тыс. у.е.) от общей площади 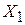 (м2), количества комнат
(м2), количества комнат 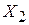 и удаленности квартиры от центра города
и удаленности квартиры от центра города 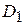 . Исходные данные приведены в табл. 5.1.
. Исходные данные приведены в табл. 5.1.
Таблица 5.1
Исходные данные
| № наблюдения | 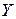
| 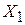
| 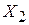
| Месторасположение квартиры | 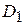
|
| 18,6 | окраина | ||||
| центр | |||||
| 14,8 | окраина | ||||
| центр | |||||
| центр | |||||
| 49,5 | центр | ||||
| 28,5 | окраина | ||||
| 24,7 | окраина | ||||
| окраина | |||||
| 33,5 | окраина | ||||
| 88,6 | 128,4 | центр | |||
| окраина | |||||
| центр | |||||
| 73,5 | окраина | ||||
| окраина |
Решение. Необходимо исследовать влияние количественных факторов 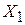 и
и 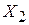 и качественного фактора
и качественного фактора 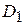 - месторасположения квартиры на рыночную стоимость квартиры
- месторасположения квартиры на рыночную стоимость квартиры 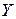 .
.
В качестве отправной точки выберем модель, содержащую только количественные факторы:
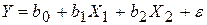 .
.
Оценивание регрессии по МНК дает следующий результат:
 .
.
Во второй строке приведены стандартные ошибки коэффициентов регрессии, а в третьей строке 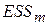 – остаточная сумма квадратов, найденная для модели с
– остаточная сумма квадратов, найденная для модели с 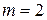 объясняющими переменными, и коэффициент детерминации
объясняющими переменными, и коэффициент детерминации 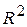 . Видно, что только коэффициент при переменной
. Видно, что только коэффициент при переменной 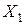 можно считать статистически значимым.
можно считать статистически значимым.
Далее будем исследовать влияние качественного фактора –месторасположения продаваемой квартиры на ее цену. Предположим, что фактор “месторасположение” может сказаться только на “начальной” цене квартиры (свободном члене). Тогда модель примет вид:
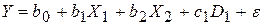 ,
,
где 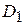 – фиктивная переменная, т.е. искусственно введенная переменная, которая принимает значение 1, если наблюдение относится к центру города, и 0, если наблюдение относится к окраине города. В табл. 4.5 показано, как вычислялись значения переменной
– фиктивная переменная, т.е. искусственно введенная переменная, которая принимает значение 1, если наблюдение относится к центру города, и 0, если наблюдение относится к окраине города. В табл. 4.5 показано, как вычислялись значения переменной 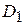 по 15 наблюдениям.
по 15 наблюдениям.
Оценивание регрессии по МНК дает следующий результат:
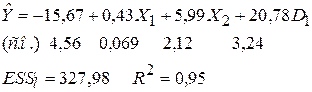
Во второй строке приведены стандартные ошибки коэффициентов регрессии, а в третьей строке 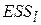 - остаточная сумма квадратов, найденная для модели с
- остаточная сумма квадратов, найденная для модели с 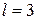 объясняющими переменными, и коэффициент детерминации
объясняющими переменными, и коэффициент детерминации 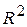 . Видно, что все эмпирические коэффициенты уравнения можно считать статистически значимыми. В частности, и коэффициент при фиктивной переменной также является статистически значимым (наблюдаемое значение
. Видно, что все эмпирические коэффициенты уравнения можно считать статистически значимыми. В частности, и коэффициент при фиктивной переменной также является статистически значимым (наблюдаемое значение 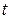 - статистики для него составляет 6,4). Другими словами, средняя цена за квартиру значимо выше (на 20,78 тыс у.е.), если квартира находиться в центре города, при неизменных значениях других факторов, включенных в модель.
- статистики для него составляет 6,4). Другими словами, средняя цена за квартиру значимо выше (на 20,78 тыс у.е.), если квартира находиться в центре города, при неизменных значениях других факторов, включенных в модель.
Полученное эмпирическое уравнение регрессии можно переписать в виде:
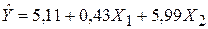 ,
,
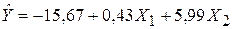 ,
,
где первая строка относится к центру города, а вторая – к окраинам.
Рассмотрим, привело ли включение фиктивной переменной к значимому повышению объясняющей способности уравнения регрессии. Остаточная сумма квадратов 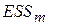 с
с 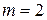 независимыми переменными составляет 1550,997, а с включением фиктивной переменной
независимыми переменными составляет 1550,997, а с включением фиктивной переменной 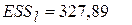 и
и 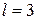 . Согласно (4.17) соответствующая
. Согласно (4.17) соответствующая 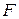 - статистика имеет вид:
- статистика имеет вид:
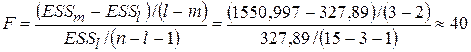
распределена с 1 и 11 степенями свободы и превышает критическое значение 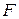 , равное 9,65 при 1%-ом уровне значимости.
, равное 9,65 при 1%-ом уровне значимости.
Таким образом, при добавлении фиктивной переменной наблюдается значительное улучшение в объяснении дисперсии зависимой переменной. Спецификация модели в целом улучшилась – коэффициент детерминации увеличился с 0,76 до 0,95.
Нелинейная регрессия
Многие взаимосвязи между экономическими показателями наилучшим образом описываются нелинейными соотношениями. Например, зависимость спроса 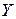 на товар от его цены
на товар от его цены 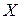 часто представляют как
часто представляют как 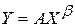 , где параметр
, где параметр 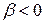 .
.
В эконометрике выделяют два класса нелинейных моделей.
К первому относят модели, нелинейные по включенным объясняющим переменным, но линейные по оцениваемым параметрам. Нелинейность по переменным устраняется путем замены переменных. Например, соотношение 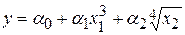 относится, очевидно, к этому классу, т.к. оно является нелинейным только по объясняющим переменным. Определим новые переменные как
относится, очевидно, к этому классу, т.к. оно является нелинейным только по объясняющим переменным. Определим новые переменные как 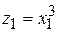 и
и 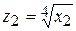 ; тогда соотношение
; тогда соотношение 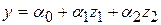 , будучи линейным по оцениваемым параметрам, становится линейным и по новым переменным. Если в рассматриваемой модели случайная компонента
, будучи линейным по оцениваемым параметрам, становится линейным и по новым переменным. Если в рассматриваемой модели случайная компонента 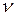 является аддитивной, т.е. выражение
является аддитивной, т.е. выражение 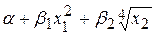 изменяется случайным образом путем уменьшения или увеличения на
изменяется случайным образом путем уменьшения или увеличения на 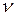 , то модель примет вид
, то модель примет вид 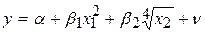 . В таком случае для нахождения оценок ее параметров применим обычный метод наименьших квадратов.
. В таком случае для нахождения оценок ее параметров применим обычный метод наименьших квадратов.
Упражнение 5.1. Исследовалась зависимость между ежегодными транспортными расходами 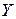 и годовым доходом
и годовым доходом 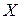 семьи. Были предложены две модели: линейная и квадратичная. Оценивание по данным для 25 семей дало следующие результаты:
семьи. Были предложены две модели: линейная и квадратичная. Оценивание по данным для 25 семей дало следующие результаты:
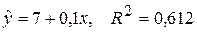 ;
;
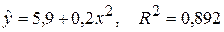 .
.
Какую из построенных моделей следует предпочесть?
Решение. В данном случае предложены две модели с одним и тем же определением зависимой переменной. Поэтому коэффициенты 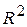 сравнимы. Результаты оценивания показывают, что линейная функция объясняет 61% дисперсии расходов на транспорт (
сравнимы. Результаты оценивания показывают, что линейная функция объясняет 61% дисперсии расходов на транспорт (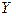 ), в то время как квадратичная зависимость объясняет уже 89% дисперсии переменной
), в то время как квадратичная зависимость объясняет уже 89% дисперсии переменной 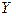 . Таким образом, квадратичная функция в наибольшей степени объясняет изменения зависимой переменной и ее следует предпочесть.
. Таким образом, квадратичная функция в наибольшей степени объясняет изменения зависимой переменной и ее следует предпочесть.
Ко второму классу относят модели, нелинейные как по объясняющим переменным, так и по параметрам. Пусть, например, экономическая зависимость моделируется формулой 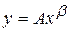 ,
, 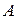 и
и 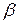 – параметры модели, подлежащие определению. Модель
– параметры модели, подлежащие определению. Модель 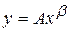 , очевидно, не является линейной как относительно переменной
, очевидно, не является линейной как относительно переменной 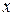 , так и параметра
, так и параметра 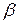 .
.
В данном случае производная 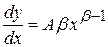 не будет константой, а будет зависеть от переменной
не будет константой, а будет зависеть от переменной 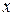 , что присуще только нелинейным моделям. Параметр
, что присуще только нелинейным моделям. Параметр 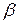 определяет эластичность переменной
определяет эластичность переменной 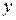 по переменной
по переменной 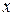 , т.е. процентное изменение
, т.е. процентное изменение 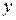 для данного процентного изменения
для данного процентного изменения 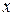 . Действительно,
. Действительно, 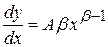 , следовательно,
, следовательно,  . Тогда
. Тогда 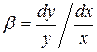 . Таким образом, параметр
. Таким образом, параметр 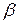 показывает на сколько процентов увеличится переменная
показывает на сколько процентов увеличится переменная 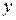 , когда значение переменной
, когда значение переменной 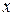 увеличится на 1 %. Степенная зависимость
увеличится на 1 %. Степенная зависимость 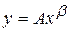 может отражать, например, соотношение между объемом выпуска продукции
может отражать, например, соотношение между объемом выпуска продукции 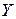 и фактором производства
и фактором производства 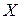 (в этом случае она называется производственной функцией), или же соотношение между спросом на некоторое благо
(в этом случае она называется производственной функцией), или же соотношение между спросом на некоторое благо 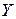 и его ценой
и его ценой 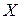 (в этом случае она называется функцией Энгеля).
(в этом случае она называется функцией Энгеля).
Стандартным подходом к линеаризации таких моделей является их логарифмирование.
Действительно, 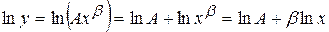 . Сделаем замену
. Сделаем замену 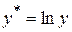 ,
, 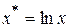 и
и 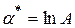 , тогда относительно новых переменных
, тогда относительно новых переменных 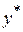 и
и 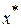 получим линейную модель
получим линейную модель  .
.
Если в рассматриваемой нелинейной модели случайная компонента 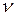 является мультипликативной, т.е. она изменяет выражение
является мультипликативной, т.е. она изменяет выражение 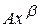 в случайной пропорции, то модель примет вид:
в случайной пропорции, то модель примет вид: 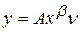 . Тогда после логарифмирования модель становится линейной и относительно логарифма случайной компоненты, следовательно, для нахождения оценок ее параметров можно применить МНК. При этом, если случайная величина
. Тогда после логарифмирования модель становится линейной и относительно логарифма случайной компоненты, следовательно, для нахождения оценок ее параметров можно применить МНК. При этом, если случайная величина 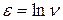 имеет нормальный закон распределения, то для анализа качества модели можно использовать
имеет нормальный закон распределения, то для анализа качества модели можно использовать 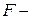 и
и 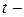 статистики.
статистики.
Если в рассматриваемой модели случайная компонента является аддитивной, т.е. 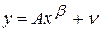 , то применять обычный метод наименьших квадратов уже невозможно. В таком случае применяют специальные итерационные процедуры.
, то применять обычный метод наименьших квадратов уже невозможно. В таком случае применяют специальные итерационные процедуры.
ЗАДАЧИ
1. Изучалась зависимость ВВП стран (Y) от объема добычи полезных ископаемых (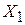 ), среднегодовой численности занятых в промышленности (
), среднегодовой численности занятых в промышленности (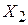 ), и годового объема сельскохозяйственного производства (
), и годового объема сельскохозяйственного производства (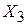 ). По выборке из 21 наблюдения проведено МНК-оценивание всевозможных многофакторных линейных моделей. Получены коэффициенты детерминации для однофакторных (I), двуфакторных (II) и трехфакторных моделей (III).
). По выборке из 21 наблюдения проведено МНК-оценивание всевозможных многофакторных линейных моделей. Получены коэффициенты детерминации для однофакторных (I), двуфакторных (II) и трехфакторных моделей (III).
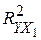 =0,33 =0,33
| 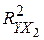 =0,39 =0,39
| 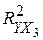 =0,42 =0,42
| (I) |
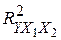 =0,41 =0,41
| 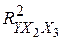 =0,51 =0,51
| 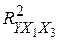 =0,66 =0,66
| (II) |
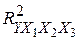 =0,67 =0,67
| (III) |
Провести отбор в модель наиболее информативных факторов.
2. Получена таблица выборочных парных коэффициентов корреляции, вычисленных по некоторым исходным данным.
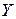
| 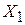
| 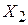
| 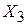
| 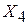
| 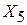
| 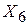
| |
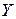
| 0,75 | 0,65 | 0,33 | 0,25 | 0,81 | 0,35 | |
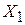
| 0,91 | 0,22 | -0,14 | 0,16 | 0,22 | ||
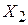
| 0,85 | 0,74 | 0,91 | 0,71 | |||
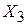
| 0,88 | 0,84 | 0,73 | ||||
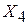
| 0,48 | 0,89 | |||||
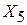
| 0,85 | ||||||
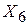
|
На основе анализа матрицы парных коэффициентов корреляции провести отбор наиболее существенных факторов в модель.
3. Исследуется зависимость суммарного балла 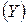 , набранного студентом-выпускником, от его суммарного балла
, набранного студентом-выпускником, от его суммарного балла 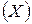 , набранного по результатам ЕГЭ, и активности в занятиях спортом. Предполагается, что активность студента в занятиях спортом описывается четырьмя уровнями градации:
, набранного по результатам ЕГЭ, и активности в занятиях спортом. Предполагается, что активность студента в занятиях спортом описывается четырьмя уровнями градации:
- не занимается никакими видами спорта и не делает зарядки по утрам;
- не занимается спортом, но делает ежедневную зарядку;
- не делает зарядку, но занимается в спортивной секции;
- делает зарядку и занимается в спортивной секции.
Сколько булевых переменных следует выбрать для описания приверженности студента занятиям спортом? Запишите общий вид линейного соотношения между суммарным баллом студента-выпускника и его суммарным баллом, набранным по результатам ЕГЭ, а также его активностью в спортивных занятиях.
4. Исследуется зависимость заработной платы 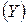 молодого специалиста от суммарного балла
молодого специалиста от суммарного балла 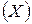 , набранного им за время учебы, и от его активности в занятиях наукой. Предполагается, что активность студента в занятиях наукой описывается тремя уровнями:
, набранного им за время учебы, и от его активности в занятиях наукой. Предполагается, что активность студента в занятиях наукой описывается тремя уровнями:
- во время учебы студент никогда не занимался научными исследованиями;
- во время учебы студент занимался научными исследованиями, но опубликованных результатов не имеет;
- результаты научных исследований студента были опубликованы.
Сколько булевых переменных следует выбрать для описания степени активности студента в занятиях наукой? Запишите общий вид линейного соотношения между зарплатой молодого специалиста и средним баллом, набранным им за время учебы, а также его активностью в занятиях наукой.
5. Исследуется зависимость рыночной цены на автомобиль определенной марки от его «возраста» и расположения руля. Предполагается, что качественный фактор D может принимать два значения:
- «правый» руль (произведен для стран с левосторонним движением) (D=0);
- «левый» руль (обычный) (D=1).
Результаты регрессии, полученные по данным выборки объемом 33 наблюдений, имеют вид:
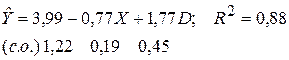
Можно ли принять, что цена на машину существенно ниже, если машина снабжена «правым» рулем?
6. Исследуется зависимость веса человека (Y, см) от его роста (X, кг) и пола. Предполагается, что качественный фактор D: пол человека – описывается двумя уровнями градации:
мужской  ;
;
женский 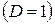 .
.
Результаты регрессии, полученные по данным выборки объемом 40 наблюдений, имеют вид:
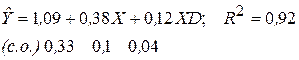
Проверить статистическую значимость эмпирических коэффициентов модели и ее качество при 5%-ом уровне значимости. На сколько в среднем увеличится вес женщины, если ее рост увеличится на 1 см? На сколько в среднем увеличится вес мужчины, если его рост увеличится на 2 см?
7. Какие из представленных моделей могут быть линеаризованы:
a) 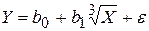 ;
;
b) 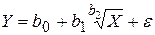 ;
;
c) 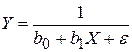 ;
;
d) 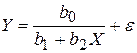 ;
;
e) 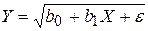 ;
;
f) 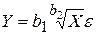 ;
;
g) 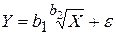 ;
;
h) 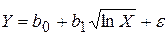 ;
;
i) 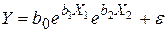 ;
;
j) 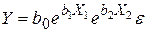 .
.
Какие из моделей являются нелинейными по включенным переменным, но линейными по параметрам?