3.7. Theorem 7 (Distributive Laws) (Распределительности)
(a) X×(Y + Z) = X×Y + X×Z and (b) X + Y×Z = (X + Y)×(X + Z) (3.7.)
Theorem 7(b) is the dual of Th7a. Let`s prove Th7b:
RHS (X + Y)×(X + Y) = X×X + X×Z + Y×X + Y×Z = X(1 + Z + Y) +Y×Z = X + Y×Z =
= LHR (multiply term by term; X×X = X Th3a; take out of the brackets X; remember that 1 + Z + Y = 1 Th1b).
As an illustration, Th7a can be used to simplify Boolean expression:
 +
+  B + A×
B + A×  +A×B =
+A×B =  × (
× ( + B) + A × (
+ B) + A × ( + B) =
+ B) = 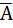 ×1 + A×1 =
×1 + A×1 = 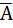 + A = 1
+ A = 1
Theorem 7(b) can be used to simplify Boolean expression:
(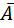 +
+ 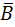 )× (
)× (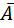 + B) × (A +
+ B) × (A + 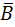 ) × (A + B) = (
) × (A + B) = (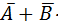 B) × (A +
B) × (A +  B) = (
B) = (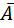 + Æ)×
+ Æ)×
× (A + Æ) = Æ.
3.8. Theorem 8. (Cклеивание по Y)
(a) X×Y + X  = X (b) (X + Y)×(X +
= X (b) (X + Y)×(X +  ) = X (3.8.)
) = X (3.8.)
This is special case of Th7 as
X×Y + X 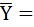 X×(Y +
X×(Y + 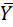 ) = X×1 =X
) = X×1 =X
This theorem, however, has another very interesting interpretation. Referring to theorem 8(a), there are two two-variable terms in the LHS expression. One of the variables, Y, is present in all possible combinations in this expression, while the other variable, X, is a common factor. The expression then reduces to this common factor. This interpretation can be usefully employed to simplify many a complex Boolean expression. As an illustration, let us consider the following Boolean expression: A× 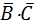 + A×
+ A× 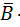 C + A×B×
C + A×B× 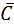 +A×B×C = A. In the above expression, variables B and C are present in all four possible combinations, and variable A is the common factor in all four product terms. With the application of theorem 8(a), this expression reduces to A. Similarly, with the application of theorem 8(b), (A+
+A×B×C = A. In the above expression, variables B and C are present in all four possible combinations, and variable A is the common factor in all four product terms. With the application of theorem 8(a), this expression reduces to A. Similarly, with the application of theorem 8(b), (A+ 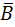 +
+  ×(A+
×(A+ 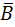 +C)×(A+B+
+C)×(A+B+ 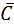 )×(A+B+C) also reduces to A as the variables B and C are present in all four possible combinations in sum terms and variable A is the common factor in all the terms.
)×(A+B+C) also reduces to A as the variables B and C are present in all four possible combinations in sum terms and variable A is the common factor in all the terms.
Theorem 9.
(a) (X + 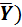 × Y = X×Y (b) X×
× Y = X×Y (b) X× 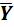 + Y = X + Y (3.9.)
+ Y = X + Y (3.9.)
3.10. Theorem 10 (Absorption Law or Redundancy Law) (Поглощения или избыточности)
(a) X + X×Y = X (b) X×(X + Y) = X (3.10.)
The proof of Th3.10a: X + X×Y = X×(1 + Y) = X×1 = X, Th3.10b is dual and hence stands proved. The crux of this simplification theorem is that, if a smaller term appears in a larger term, then the larger term is redundant. The following examples further illustrate the underlying concept:
A + A×  + A×
+ A×  ×
× 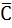 + A×
+ A×  ×C + A×B×
×C + A×B× 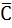 = A
= A
(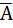 + B +
+ B + 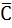 )×(
)×( + B)×(
+ B)×(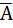 + B + C) =
+ B + C) = 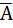 + B.
+ B.
Theorem 11
(a) Z×X + Z×  ×Y = Z×X + Z×Y
×Y = Z×X + Z×Y
(b) (Z +  + Y)× (Z + X) = (Z + X)×(Z + Y) (3.11)
+ Y)× (Z + X) = (Z + X)×(Z + Y) (3.11)
Table 3.1 gives the proof of theorem 11(a) using the method of perfect induction (truth table). Theorem 11(b) is the dual of theorem 11(a) and hence stands proved. A useful interpretation of this theorem is that, when a smaller term appears in a larger term except for one of the variables appearing as a complement in the larger term, the complemented variable is redundant. As an example,
(A+ 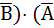 +
+  +C)×(
+C)×( +
+  +D) = (A +
+D) = (A +  )×(
)×( +C)×(
+C)×(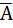 +
+  + D) =
+ D) =
=(A + 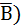 ×(
×( + C)×(
+ C)×( + D).
+ D).
Table 3.1. 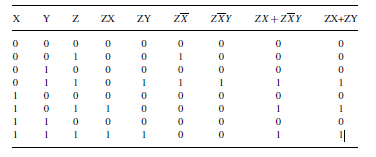
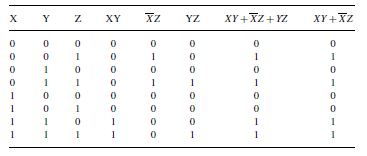
Proof of Th11a by method of perfect induction (truth table): put together three column all possible of values of variable X,Y,Z; for each combination values X,Y,Z makes up respective terms – intermediate and final; checking column final terms (Z×X +Z 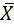 Y)(LHS) and (ZX + ZY)(RHS) Th11a.
Y)(LHS) and (ZX + ZY)(RHS) Th11a.
3.12. Theorem 12 (Consensus Theorem) (Непротиворечивости)
(a) X×Y + 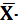 Z + YZ = X×Y +
Z + YZ = X×Y + 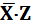
(b) (X + Y)×(  + Z)×(Y + Z) = (X + Y)×(
+ Z)×(Y + Z) = (X + Y)×(  + Z) (3.12.)
+ Z) (3.12.)
The proof of theorem 12a may be make using the method of perfect induction (Table 3.2). Theorem 12(b) is the dual of theorem 12(a) and hence stands proved. A useful interpretation of theorem 12 is as follows. If in a given Boolean expression we can identify two terms with one having a variable and the other having its complement, then the term that is formed by the product of the remaining variables in the two terms in the case of a sum-of-products expression or by the sum of the remaining variables in the case of a product-of-sums expression will be redundant. The following example further illustrates the point:
A×B×C + 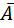 ×C×D +
×C×D +  ×C×D + B×C×D + A×C×D = A×B×C +
×C×D + B×C×D + A×C×D = A×B×C +  ×C×D +
×C×D +  ×C×D
×C×D
If we consider the first two terms of the Boolean expression, B×C×D becomes redundant. If we consider the first and third terms of the given Boolean expression, A×C×D becomes redundant.
Table 3.2. Proof theorem 12a.(Method of perfect induction).
3.13. Theorem 13. (DeMorgan`s theorem) – next lecture.
3.14. Theorem 14 (Transposition) (Перемещение, перестановка).
(a) X×Y + 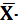 Z = (X + Z)×(
Z = (X + Z)×(  + Y) (3.14)
+ Y) (3.14)
(b) (X + Y)×(  + Z) = X×Z +
+ Z) = X×Z + 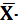 Y
Y
This theorem can be applied to any sum-of-products or product-of-sums expression having two terms, provided that a given variable in one term has its complement in the other. Table 3.3 gives the proof of theorem 14(a) using the method of perfect induction. Theorem 14(b) is the dual of theorem 14(a) and hence stands proved. As an example,
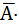 B + A×
B + A×  = (A + B)×(
= (A + B)×(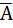 +
+  and A×B +
and A×B + 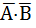 = (A+
= (A+  )×(
)×(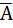 +B)
+B)
Incidentally, the first expression is the representation of a two-input EX-OR gate, while the second expression gives two forms of representation of a two-input EX-NOR gate.
Table 3.3. Proof theorem 14a.

Theorem 15.
(a) X×f(X, 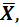 Y,Z,…) = X×f(1,0,Y,Z,…) (3.15)
Y,Z,…) = X×f(1,0,Y,Z,…) (3.15)
(b) X + f(X, 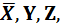 …) = X + f(0,1,Y,Z,…) (3.16)
…) = X + f(0,1,Y,Z,…) (3.16)
According to theorem 15(a), if a variable X is multiplied by an expression containing X and 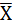 in addition to other variables, then all Xs and
in addition to other variables, then all Xs and 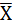 s can be replaced with 1s and 0s respectively. This would be valid as X×X = X and X×1 = X. Also, X×
s can be replaced with 1s and 0s respectively. This would be valid as X×X = X and X×1 = X. Also, X× 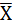 = 0 and X×0 = 0. According to theorem 15(b), if a variable X is added to an expression containing terms having X and
= 0 and X×0 = 0. According to theorem 15(b), if a variable X is added to an expression containing terms having X and 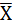 in addition to other variables, then all Xs can be replaced with 0s and all Xs can be replaced with ls. This is again permissible as X+X as well as X+0 equals X. Also, X+
in addition to other variables, then all Xs can be replaced with 0s and all Xs can be replaced with ls. This is again permissible as X+X as well as X+0 equals X. Also, X+ 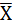 and
and 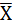 +1 both equal 1.
+1 both equal 1.
This pair of theorems is very useful in eliminating redundancy in a given expression. An important corollary of this pair of theorems is that, if the multiplying variable is 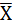 in theorem 15(a), then all Xs will be replaced by 0s and all
in theorem 15(a), then all Xs will be replaced by 0s and all 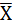 s will be replaced by ls. Similarly, if the variable being added in theorem 15(b) is
s will be replaced by ls. Similarly, if the variable being added in theorem 15(b) is 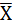 , then Xs and
, then Xs and 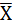 s in the expression are replaced by 1s and 0s respectively. In that case the two theorems can be written as follows:
s in the expression are replaced by 1s and 0s respectively. In that case the two theorems can be written as follows:
(a)  (3.17)
(3.17)
(b) 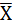 + f(X,
+ f(X, 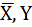 ,Z,…) =
,Z,…) = 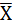 + f(1,0,Y,Z,…) (3.18)
+ f(1,0,Y,Z,…) (3.18)
The theorems are further illustrated with the help of the following examples:
1. A×[ 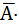 B + A×
B + A× 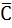 + (
+ (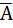 + D)×(A +
+ D)×(A +  = A×[0×B + 1×
= A×[0×B + 1× 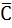 + (0 + D)×(1 +
+ (0 + D)×(1 +  )] = A×(
)] = A×(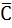 +D)
+D)
2. 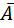 + [
+ [ 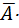 B + A×
B + A× 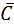 + (
+ (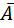 + B)×(A +
+ B)×(A +  )] =
)] = 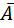 + [0×B + 1×
+ [0×B + 1× 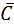 + (0 + B)×(1 +
+ (0 + B)×(1 + 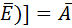 +
+ 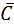 + B.
+ B.
Theorem 16.
(a) f(X,  ,Y,…,Z) = X×f(1,0,Y,…,Z) +
,Y,…,Z) = X×f(1,0,Y,…,Z) +  ×f(0,1,Y,…,Z) (3.19.)
×f(0,1,Y,…,Z) (3.19.)
(b) f(X,  ,Y,…,Z) = [X + f(0,1,Y,…,Z)]×[
,Y,…,Z) = [X + f(0,1,Y,…,Z)]×[  + f(1,0,Y,…,Z)] (3.20.)
+ f(1,0,Y,…,Z)] (3.20.)
The proof of Th16a is straightforward and is given as follows:
f(X, 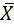 ,Y,…,Z) = X×f(X,
,Y,…,Z) = X×f(X, 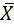 ,Y,…,Z) +
,Y,…,Z) + 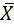 ×f(X,
×f(X, 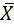 ,Y,…,Z) =
,Y,…,Z) =
X×f(1,0,Y,…,Z) + 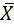 ×f(0,1,Y,…,Z) (Th15a).
×f(0,1,Y,…,Z) (Th15a).
Also
f(X, 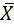 ,Y,…,Z) = [X + f(X,
,Y,…,Z) = [X + f(X, 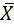 ,Y,…,Z)]×[
,Y,…,Z)]×[ 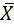 + f(X,
+ f(X, 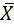 ,Y,…,Z)] =
,Y,…,Z)] =
= [X + f(0,1,Y,…,Z)]×[ 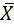 + f(1,0,Y,…,Z)] (Th15b).
+ f(1,0,Y,…,Z)] (Th15b).
3.17. Theorem 17 (Involution Law) (Двойное отрицание)
 = X
= X
Involution law says that the complement of the complement of an expression leaves the expression unchanged. Also, the dual of the dual of an expression is the original expression. This theorem forms the basis of finding the equivalent product-of-sums expression for a given sum-of-products expression, and vice versa.