Комплексные числа
П.1 Понятие комплексного числа
· Комплексным числом 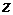 называется упорядоченная пара действительных чисел:
называется упорядоченная пара действительных чисел:  .
.
| Действительное число геометрически отождествляется с координатой точки оси. | 
|
| Комплексное число геометрически отождествляется с координатами точки на плоскости. | 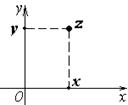
|
Множество действительных чисел (ось ОХ) является подмножеством множества комплексных чисел (плоскость ХОУ): 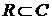 .
.
· Ось абсцисс ОХ −назовём действительной осью координатной плоскости.
При этом КЧ  отождествляется с действительным числом
отождествляется с действительным числом  :
:  .
.
· Ось ординат ОУ − назовём мнимой осью координатной плоскости.
На оси ординат(мнимая ось)лежат чисто мнимые КЧ  .
.
· Число  называется действительной частью КЧ
называется действительной частью КЧ  :
:  ,
,
 − мнимой частью КЧ
− мнимой частью КЧ  :
:  .
.
· Комплексные числа называются равными, если равны их действительные и мнимые части.
· Комплексные числа называются сопряжёнными, если их действительные части равны, а мнимые части противоположны по знаку:
 ,
, 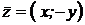 .
.
Геометрически пара сопряжённых КЧ симметрична относительно действительной оси ОХ.
Введём правила выполнения арифметических операций:
Ι. Сложение КЧ: 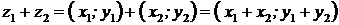 .
.
Эта операция не меняет действительное число:
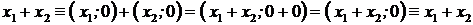 .
.
ΙΙ. Произведение КЧ:  .
.
Эта операция не меняет действительное число:
 .
.
Следствие.  .
.
► 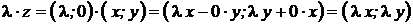 . ■
. ■
Свойства
1. Операция сложения КЧ подчиняется коммутативному и ассоциативному законам.
2. 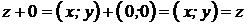 .
.
3. Операция произведения КЧ подчиняется коммутативному и ассоциативному и дистрибутивному относительно сложения законам.
4.  .
.
· КЧ 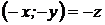 называется противоположным к числу КЧ
называется противоположным к числу КЧ  , т. к. в сумме с ним даёт нуль.
, т. к. в сумме с ним даёт нуль.
· КЧ 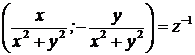 называется обратным к числу КЧ
называется обратным к числу КЧ  , т. к. в произведении с ним даёт единицу.
, т. к. в произведении с ним даёт единицу.
ΙΙΙ. Вычитание КЧ: 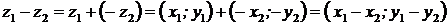 .
.
IV. Деление КЧ:
 .
.
П.2 Мнимая и действительная единицы
Оси абсцисс ОХ (действительной оси) принадлежит действительная единица:
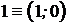 .
.
· Ось ординат ОУ (мнимая ось) содержит единицу, которую назовём мнимой единицей:  .
.
 .
.
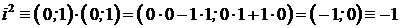



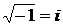 .
.
Пример. Решить уравнение 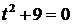 .
.
Решение.  .
.
Теорема. (основная теорема алгебры)
Каждый многочлен степени n с действительными или комплексными коэффициентами имеет n действительных или комплексных корней, среди которых могут быть и совпадающие.
Пример. Решить уравнение 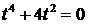 .
.
Решение. 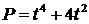 − многочлен четвертой степени имеет четыре корня.
− многочлен четвертой степени имеет четыре корня.

П.3 Алгебраическая форма записи КЧ
Рассмотрим умножение действительного числа на мнимую единицу:
 .
.
Тогда преобразуем  .
.
Получили алгебраическую форму записи КЧ: 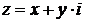 ,
,
где  и
и  – действительные числа.
– действительные числа.
 − алгебраическая форма записи сопряжённого КЧ.
− алгебраическая форма записи сопряжённого КЧ.
Алгебраическая форма записи КЧ позволяет упростить применение формул арифметических действий над КЧ:
1. Сложение КЧ
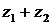
| 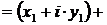  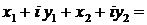
 . .
|
2. вычитание КЧ

| 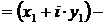  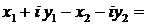
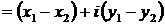 . .
|
3. Умножение КЧ

| 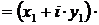  
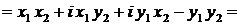  . .
|
4. Деление КЧ

| 
  . .
|
* Обратное КЧ
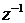
|  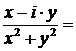  . .
|
Например. Дано КЧ  . Найти
. Найти 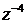 .
.
Решение. 
Найдём частное комплексных чисел:

В итоге имеем: 
Арифметическая форма КЧ позволяет доказать свойства сопряжения КЧ:
1. 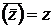 .
2. .
2.  .
3. .
3.  . .
| 4.  .
5. .
5. 
|
п.4 Тригонометрическая форма записи КЧ
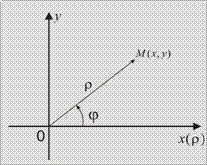 Всякое комплексное число
Всякое комплексное число  можно изобразить точкой
можно изобразить точкой  на плоскости, положение которой может определяться полярными координатами: длиной радиус-вектора
на плоскости, положение которой может определяться полярными координатами: длиной радиус-вектора 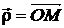 =
=  , который с положительным направлением оси ОХ образует угол
, который с положительным направлением оси ОХ образует угол  .
.
· Длина вектора  называется модулем КЧ
называется модулем КЧ
и обозначается  .
.
· Величина угла между положительным направлением действительной оси и вектором  называется аргументом КЧ и обозначается
называется аргументом КЧ и обозначается  .
.
Аргумент КЧ есть величина многозначная:  (
(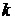 – целое),
– целое),
где  – главное значение аргумента,
– главное значение аргумента, 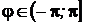 .
.
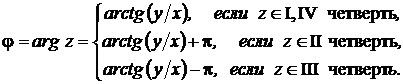
Учитывая формулы связи полярных  и декартовых
и декартовых  координат точки плоскости:
координат точки плоскости: 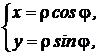 комплексное число можно представить в виде:
комплексное число можно представить в виде:
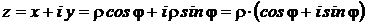 .
.
Т. о. получили тригонометрическую форму записи КЧ:  .
.
Очевидно, что комплексно-сопряженные числа имеют одинаковые модули и противоположные аргументы: 
Например. Число  представим в тригонометрическом виде.
представим в тригонометрическом виде.

Тогда 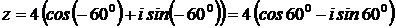 .
.
Тригонометрическая форма записи КЧ позволяет упростить применение формул арифметических действий над КЧ:
1. Умножение КЧ 
| 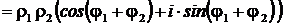 . .
|
* Возведение в степень

|  – формула Муавра.
Абрахам де Муавр (1667-1754) – английский математик
– формула Муавра.
Абрахам де Муавр (1667-1754) – английский математик
|
2. Деление КЧ 
|  . .
|
3. Извлечение корня 
| Для любого КЧ 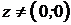 корень корень  -ой степени имеет ровно -ой степени имеет ровно  различных значений: различных значений:
 ,
где ,
где  Корни
Корни  -ой степени из КЧ являются вершинами правильного -ой степени из КЧ являются вершинами правильного  -угольника, вписанного в окружность с центром в начале координат и радиуса -угольника, вписанного в окружность с центром в начале координат и радиуса  . .
|
Доказательства.
1) 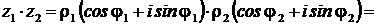


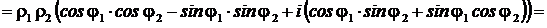
 . ■
. ■
2) 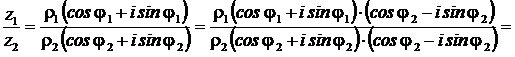

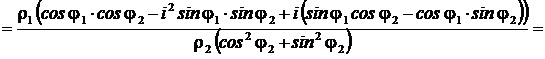

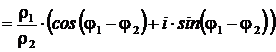 . ■
. ■
3) Пусть  .
.
Возводя в степень 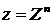 , получим:
, получим:  .
.
Отсюда: 
Или: 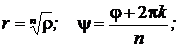 где
где  ,
,
Т. о.  .
.
Учитывая периодичность функций синуса и косинуса, корень n -ой степени из комплексного числа имеет n различных значений, т. е. при  . ■
. ■
Пример 1.  . Найти
. Найти  ,
,  .
.
Решение.
1) Учитывая пример стр.5, имеем  .
.
Для нахождения  воспользуемся формулой Муавра:
воспользуемся формулой Муавра:
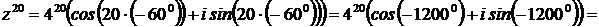
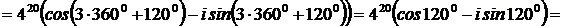

2) 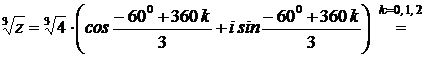
 Посмотрим на чертеже расположение найденных корней:
Посмотрим на чертеже расположение найденных корней:
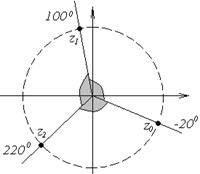
| Корни являются вершинами правильного 3-угольника, вписанного в окружность с центром в начале координат и радиуса  . .
|
Замечания.
1) Равенство  , записанное в виде:
, записанное в виде:  , представляет собой уравнение окружности с центром в начале координат и радиуса
, представляет собой уравнение окружности с центром в начале координат и радиуса  . Тогда:
. Тогда:
ü уравнение  или
или 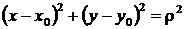 − геометрическое место точек
− геометрическое место точек 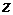 , лежащих на окружности с центром в точке
, лежащих на окружности с центром в точке  и радиуса
и радиуса  ;
;
ü неравенство  − геометрическое место внутренних точек
− геометрическое место внутренних точек 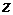 круга с центром в точке
круга с центром в точке  и радиуса
и радиуса  .
.
2) Равенство  представляет собой формулу для вычисления расстояния между точками
представляет собой формулу для вычисления расстояния между точками 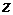 и
и  . Тогда:
. Тогда:
ü уравнение 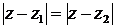 задаёт равенство расстояний от точки
задаёт равенство расстояний от точки 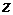 до точек
до точек  и
и 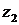 , что определяет ГМТ
, что определяет ГМТ 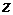 , принадлежащих серединному перпендикуляру к отрезку, соединяющему точки
, принадлежащих серединному перпендикуляру к отрезку, соединяющему точки  и
и 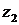 ;
;
ü неравенство 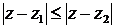 определяет ГМТ
определяет ГМТ 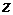 , принадлежащих полуплоскости с граничной прямой − серединный перпендикуляр к отрезку, соединяющему точки
, принадлежащих полуплоскости с граничной прямой − серединный перпендикуляр к отрезку, соединяющему точки  и
и 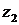 , и содержащей точку
, и содержащей точку  .
.