Постановка задачи
Пусть требуется решить систему n нелинейных уравнений:
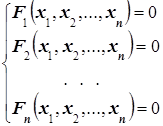 (1)
(1)
Прямых методов решения системы (1) не существует. Лишь в отдельных случаях эту систему можно решить непосредственно. Например, для случая двух уравнений иногда удаётся выразить одну неизвестную переменную через другую и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного.
Систему уравнений (1) можно кратко записать в векторном виде:
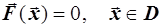 . (2)
. (2)
Уравнение (2) может иметь один или несколько корней в области определения D. Требуется установить существование корней уравнения и найти приближённые значения этих корней. Для нахождения корней обычно применяют итерационные методы, в которых принципиальное значение имеет выбор начального приближения. Начальное приближение иногда известно из физических соображений. В случае двух неизвестных начальное приближение можно найти графически: построить на плоскости (x1, x2) кривые f1(x1, x2)=0 и f2(x1, x2)=0 и найти точки их пересечения. Для трех и более переменных (а также для комплексных корней) удовлетворительных способов подбора начального приближения нет.
Рассмотрим два основных итерационных метода решения системы уравнений (1), (2) - метод простой итерации и метод Ньютона.
Методы решения системы нелинейных уравнений
Метод простой итерации
Представим систему (1) в виде
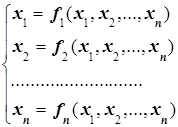 (3)
(3)
или в векторной форме:
 (4)
(4)
Алгоритм метода простой итерации состоит в следующем. Выберем некоторое нулевое приближение

Следующее приближение находим по формулам:

или более подробно:
 (5)
(5)
Итерационный процесс (5) продолжается до тех пор, пока изменения всех неизвестных в двух последовательных итерациях не станут малыми, т.е.
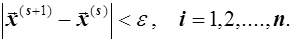
На практике часто вместо последнего условия используют неравенство:
 (6)
(6)
где 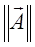 - среднеквадратичная норма n-мерного вектора
- среднеквадратичная норма n-мерного вектора  , т.е.
, т.е.
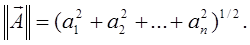
При использовании данного метода успех во многом определяется удачным выбором начального приближения  : оно должно быть достаточно близким к истинному решению. В противном случае итерационный процесс может не сойтись. Если процесс сходится, то его скорость сходимости является линейной.
: оно должно быть достаточно близким к истинному решению. В противном случае итерационный процесс может не сойтись. Если процесс сходится, то его скорость сходимости является линейной.
Метод Ньютона
В переводной литературе можно встретить название метод Ньютона-Рафсона. Этот метод обладает гораздо более быстрой сходимостью, чем метод простой итерации.
Пусть известно некоторое приближение 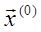 к корню
к корню 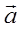 , так что
, так что

Тогда исходную систему (2) можно записать следующим образом:
Разлагая уравнение (7) в ряд Тейлора в окрестности точки  и ограничиваясь линейными членами по отклонению
и ограничиваясь линейными членами по отклонению  , получим:
, получим:
 ,
,
или в координатной форме:
 (8)
(8)
Систему (8) можно переписать в виде:
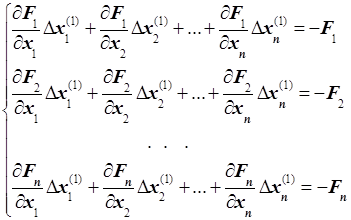 (9)
(9)
Полученная система (9) является системой линейных алгебраических уравнений относительно приращений
 .
.
Значение функций F1, F2, …, Fn и их производные в (9) вычисляются при
 .
.
Определителем системы (9) является якобиан J:
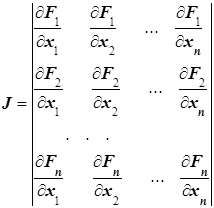 (10)
(10)
Для существования единственного решения системы уравнений (9) он должен быть отличен от нуля. Решив систему (9), например, методом Гаусса, найдём новое приближение:
 .
.
Проверяем условие (6). Если оно не удовлетворяется, находим  и якобиан (10) с новым приближением и опять решаем (9), таким образом, находим 2-е приближение и т.д.
и якобиан (10) с новым приближением и опять решаем (9), таким образом, находим 2-е приближение и т.д.
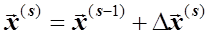
Итерации прекращаются, как только выполнится условие (6).
Задание
Используя метод Ньютона, найдите решения системы нелинейных уравнений с заданной точностью  . Исследуйте сходимость итерационного процесса.
. Исследуйте сходимость итерационного процесса.
Варианты заданий
1  2
2 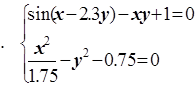
3  4
4 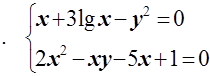
5  6
6 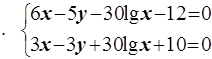
7  8
8 
9 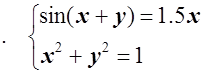 10
10 
11  12
12 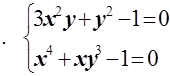
13 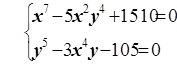 14.
14. 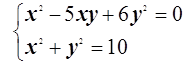
15.  16.
16. 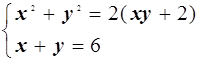
17. 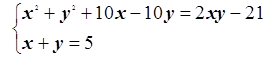 18.
18. 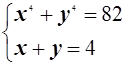
19. 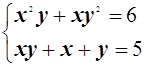 20.
20. 
21.  22.
22. 