Введение
Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.
В конце прошлого века в работах Пуанкаре и Клейна была установлена прямая связь геометрии Лобачевского с теорией функций комплексной переменной и с теорией чисел (точнее, арифметикой неопределенных квадратичных форм). С тех пор аппарат геометрии Лобачевского стал неотъемлемым компонентом этих разделов математики. В последние 15 лет значение геометрии Лобачевского еще более возросло благодаря работам американского математика Тёрстона (лауреата Филдсовской медали 1983 г.), установившего ее связь с топологией трехмерных многообразий. Десятки работ ежегодно публикуются в этой области. Современные исследования все больше требуют делового владения геометрией Лобачевского.
Я выбрала данную тему по нескольким причинам:
1. Теория геометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир.
2. Это интересный, необычный и прогрессивный раздел современной геометрии.
3. Она дает материал для размышлений – в ней не все просто, не все ясно с первого взгляда, чтобы ее понять, нужно обладать фантазией и пространственным воображением.
Я поставила перед собой такие задачи, как рассмотреть историю возникновения неевклидовой геометрии, познакомиться с личностью Лобачевского и его работой и определить значение геометрии Лобачевского в современной науке.
Геометрия Лобачевского
Рассмотрим основные понятия, на которых базируется изложение геометрии Лобачевского. За основные объекты приняты точка, прямая и отрезок. За основные отношения между этими объектами принимаются:
Точка принадлежит фигуре, в частности прямой;
Точка лежит между двумя точками для точек прямой.
Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками. Эти точки называются концами отрезка.
Лучом AB называется часть прямой, состоящая из всех ее точек, лежащих по ту же сторону от точки А, что и точка В. точка А называется вершиной луча.
Углом называется фигура, которая состоит из точки – вершины угла и двух различных лучей, исходящих из этой точки, - сторон угла.
Аксиоматика Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского.
Воображаемой геометрией Лобачевский назвал ее потому, что она пока оставалась доступной лишь воображению, а не опыту.
Если вместо V постулата допустить, что для пары «точка—прямая» V постулат неверен, то полученная система аксиом будет описывать геометрию Лобачевского. Понятно, что в геометрии Лобачевского все эквивалентные V постулату Евклида утверждения неверны.
V постулат в Геометрии Лобачевского: на плоскости через точку, не лежащую на данной прямой, проходит не менее двух прямых, не пересекающая данную (рисунок 3).
Рисунок 3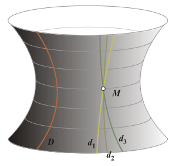 
Наглядное представление геометрии Лобачевского: через точку M проходят две прямые, параллельные прямой D.
Параллельные и расходящиеся прямые
Лобачевский изменил само понимание параллельных линий. У Евклида непересекающиеся и параллельные — одно и то же, у Лобачевского: из всех, не пересекающих данную прямую АВ, лишь две прямые называются параллельными, при этом различают направление параллельности.
Параллельность прямых на евклидовой плоскости можно характеризовать и другими свойствами, например, наличием у них многих общих перпендикуляров или постоянством длин этих перпендикуляров.
На плоскости Лобачевского для двух непересекающихся прямых эти утверждения неверны. Здесь возможны два случая: прямые имеют общий перпендикуляр и прямые не имеют общего перпендикуляра
Рисунок 4
Поэтому постулат уточняется: если дана прямая АВ и не лежащая на ней точка М, то через точку М в плоскости МАВ можно провести две прямые, параллельные данной прямой АВ. Параллельными Лобачевский, следовательно, называет такие, которые отделяют непересекающие от пересекающих данную прямую АВ. Расстояние между прямой АВ и каждой из параллельных не остается постоянным — уменьшается в сторону параллелизма и увеличивается в противоположную сторону. Параллельные прямые могут близко подойти друг к другу, но они не могут пересечься.
Плоскость, в которой существуют такие параллельные, принято называть плоскостью Лобачевского. Эта плоскость вовсе не «плоская» в евклидовом смысле. В евклидовой плоскости угол параллельности неизменен и всегда равен 90°; в геометрии Лобачевского он может принимать все значения — от 0 до 90°. Следовательно, евклидова геометрия есть частный (предельный) случай геометрии Лобачевского, в которой угол параллельности переменный. Геометрически величина угла параллельности зависит от длины перпендикуляра MN; то есть если перпендикуляр уменьшается, угол параллельности увеличивается, постепенно приближаясь к 90°.
Таким образом, в новой геометрии существует взаимозависимость величины угла и длины отрезка. Для точки М, находящейся от заданной прямой на расстоянии MN = a (рис. 4), Лобачевский определил формулу для угла параллельности φ= П(a):
где k— постоянная, определяющая фиксированный по величине отрезок. Она получила название радиуса кривизны пространства Лобачевского. Подобно сферической геометрии существует бесконечное множество пространств Лобачевского, различающихся величиной k.
Эта зависимость называется функцией Лобачевского. Величина константы kзависит от конкретных физических условий в данной части мирового пространства. Исключительно большая величина константы свидетельствует о том, что наше пространство обладает огромным радиусом кривизны и, следовательно, довольно малой, близкой к нулю, кривизной, то есть пространство в нашей части вселенной имеет плоский, евклидов характер.
В геометрии Лобачевского сохраняются все теоремы, которые в евклидовой геометрии можно доказать без использования пятого постулата. Например, вертикальные углы равны; углы при основании равнобедренного треугольника равны; из данной точки можно опустить на данную прямую только один перпендикуляр и др. Однако теоремы, где применяется аксиома параллельности, видоизменяются.
Приведём (в современных обозначениях) несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.
- Теорема о сумме углов треугольника: В геометрии Лобачевского сумма углов любого треугольника меньше 180°. Разность между 180° и суммой углов треугольника положительна и называется дефектом (D) этого треугольника. Формула для площади треугольника S =k*D, то есть площадь связана с его дефектом. Самую большую площадь имеет треугольник с нулевыми углами, а его стороны имеют бесконечную длину (рисунок 5).
Рисунок 5
- Два неравных равносторонних треугольника имеют неравные углы.
- В геометрии Лобачевского не существует подобных фигур.
- Если углы одного треугольника равны соответственно углам другого треугольника, то эти треугольники равны.
- Геометрическое место точек, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону есть кривая линия, которая называется эквидистантой.
- Через точку, не лежащую на данной прямой проходит бесконечно много прямых, не пересекающихся с данной, среди них две параллельные прямые в смысле Лобачевского, при этом мы должны отличать ещё сторону параллельности
- Если прямые имеют общий перпендикуляр, то они расходятся
- В геометрии Лобачевского существует зависимость между углами и длиной сторон треугольника.
- Длина окружности не пропорциональна ее радиусу, а растет быстрее.
Возможные расположения двух прямых на плоскости Лобачевского: две несовпадающие прямые либо пересекаются в одной точке, либо параллельны, либо являются расходящимися (рис 6).
Рисунок 6
В заключение отметим, что Лобачевский с исчерпывающей полнотой развил все разделы своей неевклидовой геометрии, включая тригонометрию и начала аналитической и дифференциальной геометрии.
Доказательство независимости пятого постулата (построение моделей)
Доказать непротиворечивость новой геометрии ни Лобачевский, ни Бойяи не сумели — тогда математика ещё не располагала необходимыми для этого средствами. Только спустя 40 лет появились исследования Э. Бельтрами (1868), модель Клейна (1871) и модель Пуанкаре (1882), реализующие аксиоматику геометрии Лобачевского на базе евклидовой геометрии.
В 1871 году Клейн предложил первую полноценную модель плоскости Лобачевского.
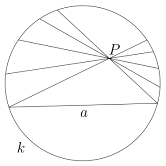
Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, так как через точку P, не лежащую на данной хорде а (то есть «прямой»), проходит сколько угодно не пересекающих её хорд («прямых») (например, b, b').
Позже Пуанкаре, в связи с задачами теории функций комплексного переменного дал другую модель. За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.
Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.
Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.
Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.
Длина окружности не пропорциональна радиусу, а растёт быстрее.
Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия.
В 1868 году итальянский математик Э. Бельтрами исследовал поверхность c постоянной отрицательной кривизной, называемую псевдосферой и доказал, что на этой поверхности действует геометрия Лобачевского.
|
Трактриса
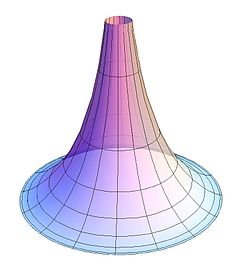
Рисунок 7 - Псевдосфера
Однако здесь даётся интерпретация геометрии только локально, то есть на куске, а не на всей плоскости Лобачевского.
Геометрия Лобачевского в реальном мире
Если геометрия Евклида является только частью геометрии Лобачевского, то выходит, что наш мир – не мир Евклида. Почему же мы не замечаем разницы. Рассмотрим такое понятие как гауссова кривизна пространства. Если мы возьмем кривую поверхность, проведем к какой-то точке касательную, проведем в точку касания отрезок, перпендикулярный касательной плоскости, то мы получим нормаль. Проведя через нормаль плоскость, мы можем найти окружность, наиболее плотно прилегающую к поверхности. Так как мы можем провести сколько угодно плоскостей, то мы можем найти окружности с минимальным и максимальным радиусами. Используя определенные соотношения, можно определить кривизну пространства, которая может быть как положительная, так и отрицательная. На поверхностях с отрицательной кривизной и работает геометрия Лобачевского. Именно такую кривизну имеют графики интенсивности всех электромагнитных полей. Состояние поверхности плазмы также описывается геометрией Лобачевского.
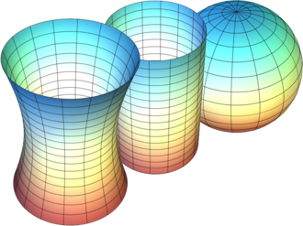
Рисунок 9 - Поверхности с отрицательной (слева), нулевой (в центре) и положительной (справа) кривизной
Сам Лобачевский применил свою геометрию к вычислению определённых интегралов.
Геометрия Лобачевского находит применение также в теории чисел, в её геометрических методах, объединённых под названием «геометрия чисел».
Была установлена тесная связь геометрии Лобачевского с кинематикой специальной (частной) теории относительности. Эта связь основана на том, что равенство, выражающее закон распространения света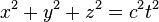 
при делении на 
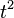, то есть для скорости света, даёт
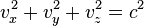
— уравнение сферы в пространстве с координатами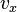 
, 
, 
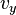— составляющими скорости по осям х, у, z (в «пространстве скоростей»). Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с, то есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.
Замечательное приложение геометрия Лобачевского нашла в общей теории относительности. Если считать распределение масс материи во Вселенной равномерным (это приближение в космических масштабах допустимо), то оказывается возможным, что при определённых условиях пространство имеет геометрию Лобачевского. Таким образом, предположение Лобачевского о его геометрии как возможной теории реального пространства оправдалось.
Значение геометрии Лобачевского для космологии было выявлено А. А. Фридманом. В 1922 он нашел решение уравнения Эйнштейна, из которого следовало, что Вселенная расширяется с течением времени. Метрика, найденная А. А. Фридманом, дает при фиксированном времени пространство Лобачевского. Пространство скоростей специальной теории относительности является пространством Лобачевского. Геометрия Лобачевского с успехом используется при изучении столкновений элементарных частиц и при разработке др. вопросов ядерных исследований.
Создание геометрии Лобачевского явилось важным этапом в развитии учения о возможных свойствах пространства. Особенное значение это имело для оснований математики, т. к. принципы современного аксиоматического метода вырабатывались в значительной степени благодаря появлению геометрии Лобачевского
Через некоторое время идеи Лобачевского были приняты математиками, и следующим этапом развития геометрии стала эллиптическая геометрия Римана. Риман исходил из того, что через точку, не лежащую на данной прямой, вообще нельзя провести прямую, не пересекающую данную.
В геометрии Римана:
· Две прямые всегда пересекаются, параллельных прямых совсем нет;
· Сумма углов прямолинейного треугольника больше 180°;
· Прямая имеет конечную длину, плоскость – конечную площадь и др.
Частным случаем эллиптической геометрии Римана является сферическая геометрия Римана или геометрия не сфере.
Примеры поверхностей Лобачевского
Для поверхности Лобачевского необходима постоянная отрицательная кривизна во всех её точках. Известно множество различных вариантов таких поверхностей:
Рисунок 10 - Псевдосферические поверхности
В литературе описаны разнообразные псевдосферические поверхности вращения:
Рисунок 11- Псевдосферические поверхности вращения
Многие поверхности постоянной отрицательной кривизны названы именами математиков, которые их исследовали и описали:
Рисуно12 Поверхность Дини (слева) и поверхность Бианки - Амслера (справа)
На приведённых рисунках видно, что поверхности постоянной отрицательной кривизны либо имеют край, либо замкнуты.
Кривизна пространства проявляется в больших масштабах и вблизи массивных космических тел, а в повседневной жизни на нашей планете мы можем с успехом пользоваться геометрией Евклида с большой точностью, так как нелинейные поправки на кривизну пространства ничтожно малы.
Заключение
Хотя Лобачевский доказал, что геометрия Евклида не является единственно возможной, однако это не подорвало незыблемость геометрии Евклида.
В основе геометрии Евклида лежат понятия и аксиомы, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок развитию науки, способствовало более глубокому пониманию окружающего нас материального мира.
Ученых издавна волновал вопрос – в каком мире мы живем? Какой геометрией он описывается? Сейчас вселенная расширяется, но если масса вещества всей вселенной превысит определенный порог, то расширение сменится сжатием, то есть пространство будет искривлено таким образом, что луч света, однажды покинув одну точку, вернется обратно, а это значит, мы живем в мире эллиптической геометрии Римана. Если массы не хватит, то вселенная будет расширяться неограниченно, а значит, мы живем в мире гиперболической геометрии Лобачевского
Я считаю, что я достигла цели, которую поставила в своей работе. Я получила представление о стройной теории – геометрии Лобачевского, при этом я получила навыки исследовательской деятельности, активно включился в процесс познания и творческой реализации.
Список литературы
Н.И. Лобачевский Полное собрание сочинений, том первый, Геометрические исследования по теории параллельных линий. О началах геометрии, под ред. В.Ф.Каган,1946.
Колесников М. Лобачевский. Серия «Жизнь замечательных людей». – М.: Молодая гвардия, 1965
Широков П.А. Краткий очерк основ геометрии Лобачевского. /. – М.: Наука, 1983.
Бобров С.П. Волшебный двурог. /. М., Детская литература., 1967.