Опр. 1. Пусть даны два множества А ≠ ø и В ≠ ø и установлено какое-либо правило f или закон, по которому каждому элементу х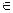 
А ставится в соответствие вполне определённый этим правилом элемент у = f (х) из множества В. Тогда говорят, что задано отображение (или функция) множества А в В и пишут
; A ® B или у = f (x), где х Î А, у Î В.
Таким образом, под отображением (функций) понимают тройку А, В и f, где А ≠ ø, В ≠ ø и при этом f осуществляет однозначное соответствие между множествами А и В.
Примеры:
1) А=В= R, где R – множество вещественных чисел,
2) f (x)= sin x или sin: R 
R, 
[-1; 1]
3) А – множество всех прямоугольников, В = R. Выберем единицу измерения и поставим в соответствие каждому прямоугольнику число – периметр этого прямоугольника.Получим отображение А 
R.
4) ортогональная проекция f 0 : А → В
Опр. 2. Два отображения 
и 
называют равными и пишут
(
), если
(
Пример:
1) A 1= R, B 1 = R+ = [0; +¥), f 1(x) = 
2) A 2 = R, B 2 = R+, f 2(x) =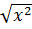 
.
Т.к. | x | = 
, то 
и потому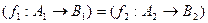 
Опр. 3. Графиком функции f: A 
B - называется множество пар вида (х, f (x)), х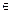 
А.
Примеры графиков функций известны из курса математики средней школы.
Опр. 4. Если f: A B таково, что А, В 
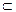R (где R – множество вещественных чисел), то функция называется числовой. При этом А называют областью определения, а В – множеством значений числовой функции.
Область определения числовой функции иногда обозначают D (f), а множество её значений Е (f); в записи у = f (x), x 
, x называют аргументом или независимой переменной, а у – зависимой переменной для функции f.
Чтобы задать конкретную числовую функцию нужно задать множества D (f), Е (f) и закон f. Поэтому, например, функции у = x 2, x Î [2; 5] и у = x 2, x Î(-¥;4] различны.
Наиболее широко применяются следующие способы задания функций: табличный, аналитический, графический.
При любом способе задания функции каждому элементу х 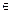D (f) ставится в соответствие единственный элемент f (x) 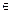E (f). Поэтому можно сказать, что f определяет множество Гf упорядоченных пар чисел, т.е.
Гf = 
D (f), f (х) 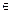E (f)}= D (f) 
E (f), где D (f) Ox,а E (f) Oу.
Тогда Гf - график можно изображать в декартовой системе координат Оху.
Если множество D (f) конечное, то такую функцию можно задать перечислением всех элементов (всех пар) множества С = D (f) Е (f), т.е. табличным способом. Так, например, в результате измерения температуры воздуха на метеорологической площадке в определённый день через равные промежутки времени получается таблица зависимости температуры Т от времени t.
Числовые функции чаще всего задаются аналитическим способом, т.е. с помощью формулы, содержащей указания на те операции, которые надо произвести над аргументом х, чтобы получить соответствующие значение функции f (x).
Пример. f (x)= 
При этом, если область задания D (f) функции не указана, то считают, что f задана для всех х, при которых возможны указания в формуле операции. Множество этих значений аргумента функции называют областью определения аналитического выражения.
Например, если у =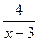 
, то (-¥; 3) È (3; +¥) - область аналитического задания.
Рассмотренные выше функции являются элементарными функциями или их комбинациями. К элементарным функциям относятся:
1. Степенная функция
Степенной функцией называется функция вида f (x) = x a, где а – любое вещественное число, называемое показателем степени.
Область определения – вся вещественная ось, т.е. D (f): х Î (-¥; +¥).
Область значений Е (f):
а - нечетное, т.е. а = 2 п +1, где п –натуральное число (n Î N), то y Î (-¥; +¥).
а - четное, т.е. а = 2 п, где п –натуральное число (n Î N), то y Î [0; +¥).
а - дробное, т.е. а = т / п, где п –натуральное число (n Î N), т -целое (т Î Z), то y Î [0; +¥).
а - отрицательное, как обратная пропорциональность т.е. y Î [0; +¥).
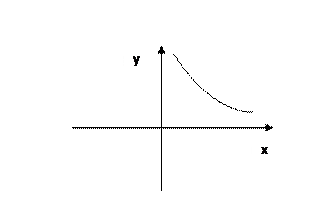
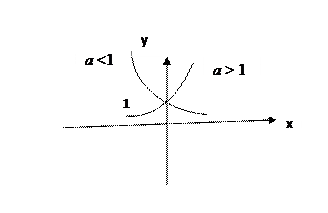
2. Показательная функция.
Показательной функцией называется функция вида f (x) = а х, где
а > 0, a ¹ 1 и называется основанием степени.
Область определения – вся вещественная ось, т.е. D (f): х Î (-¥; +¥).
Область значений Е (y): y Î [0; +¥).
3. Логарифмическая функция.
Логарифмической функцией называется функция вида f (x) =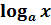 
, где
а > 0, a ¹ 1 и называется основанием степени.
Область определения – D (f): х Î [0; +¥).
Область значений Е (y): y Î (-¥; +¥).
4. Тригонометрические функции
Функция синус имеет вид: f (x) = sin x
Область определения – D (f): х Î (-¥; +¥).
Область значений Е (y): y Î [-1; 1]
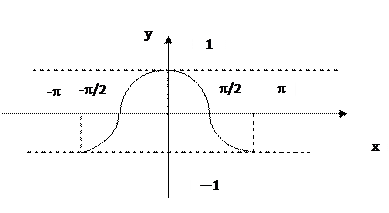
Функция сосинус имеет вид: f (x) = cos x
Область определения – D (f): х Î (-¥; +¥).
Область значений Е (y): y Î [-1; 1]
Функция тангенс имеет вид: f (x) = tg x
Область определения – D (f): х Î [-p/2; +p/2].
Область значений Е (y): y Î (-¥; ¥)
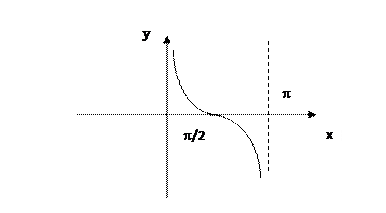
Функция тангенс имеет вид: f (x) = ctg x
Область определения – D (f): х Î [0; +p].
Область значений Е (y): y Î (-¥; ¥)
В некоторых случаях числовая функция задаётся на различных числовых промежутках различными формулами.
Пример.
1) f (x)=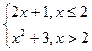 
3) f (x)= sign x =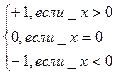 
Здесь область определения: D (f) = R, а область значений: Е (f)={-1,0,1}
4) f (x)=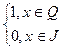 
здесь D (f) = R, E (f)= {0; 1}
Эта функция называется функцией Дирихле.
На практике часто пользуются геометрическим или графическим способом задания функции. Этот способ удобен,когда аналитически задать функцию довольно трудно.
Замечание. Геометрический образ функции f не всегда является кривой в обычном смысле. Например, у = [ x ], x 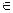R,- целая часть числа х, которую можно записать в виде у = n, n £ x < n +1, n Z (где Z – множество целых чисел). График её представлен на рисунке
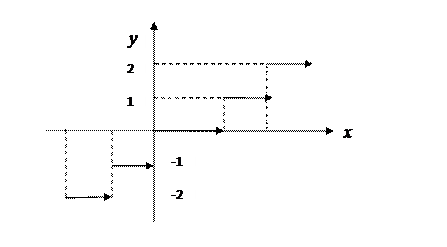
Встречаются функции,графики которых вообще изобразить нельзя, например, функция Дирихле, в силу плотности множества R.
Опр. 5. Функция y = f (x) называется убывающей (невозрастающей) если из того что х 1 > х 2 (х 1 ³ х 2) следует что f (x 1) < f (x 2) (f (x 1) £ f (x 2)).
Примером является функция f (x) = ctgx.
Опр. 6. Функция y = f (x) называется возрастающей (неубывающей) если из того что х 1 > х 2 (х 1 ³ х 2) следует что f (x 1) > f (x 2) (f (x 1) ³ f (x 2)).
Примером является функция f (x) = tgx.
Опр. 7. Функция y = f (x)называется четной, если выполняется условие
f (- x) = f (x).
Например функция f (x) = x 2 является четной, т.к. f (- x) = (- x)2 = х 2 = f (x).
Опр. 8. Функция y = f (x)называется нечетной, если выполняется условие
f (- x) = - f (x).
Например, функция f (x) = x 3 является четной, т.к. f (- x) = (- x)3 = - х 3 = - f (x).
Опр. 9. Функция y = f (x)называется периодической, если выполняется условие
f (x + Т) = f (x), где Т постоянная величина.
Например, функция f (x) = sin x является четной, т.к.
f (x+ 2p) = sin(x+ 2p) = sin х = f (x).
Опр. 10. Пусть f: A B и g: B C. Композицией отображений f и g называется функция, обозначаемая g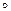 
f: A C и определяемая следующим образом: (g 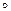f)(x) = g (f (x)), x 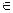A, т.е. значение композиции в точке х 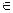А вычисляется в результате последовательного действия сначала f, а затем функции g. Функцию g (f (x)) называют также сложной функцией.
Пример. Пусть f: R R и f (x)= sin x, g: R R и g (x)= x 
.
Тогда (g 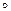f)(x) = sin x, a (f 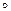у)(х)= sinx .
Следовательно, в общем (g 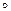f) 
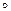(f g)
Опр. 11. Отображение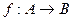 
- называется обратимым, если существует отображение 
такое, что
(f - 1 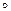f)(x) = x, для любых х Î А, и (f - 1 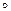f)(у) = у, для любых у Î В
При этом отображении 
называется обратным к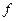 
Замечание. Определение 6 симметрично по 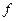и , т.е. тоже обратимо и 
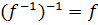. Т.о. 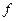и являются взаимно обратными. На основе определения 6 получается:
Теорема 1.1. Для того, чтобы отображение 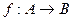было обратимым, необходимо и достаточно, чтобы между множествами А и В было установлено взаимооднозначное соответствие, т.е. элементу множества А соответствовал строго один элемент множества В, а элементу множества В соответствовал строго один элемент множества А.
Для числовых функций y= f (x), x Î A, y Î B в случае обратимости 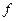получаем, что x = f -1(y). Если для обратного отображения перейти к привычным обозначениям, т. е. аргумент обозначить через «
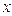», а значение функции через «у », то получаем y= f -1(x) Такое переименование переменных соответствует преобразованию симметрии относительно биссектрисы I и III квадрантов декартовой системы координат 
и, следовательно, в случае y= f (x) и y= f - 1(x) графики взаимно обратных функций расположены симметрично относительно биссектрисы I и III координатных углов (т.е. прямой у = х).
Схема построения обратной функции.
Рассмотрим функцию у = х 2, определенную на положительной полуоси, т.е. D (f): х Î [0; ¥) с областью значений Е (f): у Î [0; ¥).
Найдем обратную функцию к заданной. Для этого выразим из данной функции х: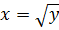 
(перед корнем выбираем «+» т.к. функция определена на положительной полуоси).
Переобозначим «х » через «у », а «у » через «х », получим: 
Представим полученные функции графически.
Примеры.
1) 
- не является обратимым
2) 
- обратима и 
3) 
- обратима
4) 
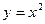не обратима на всей вещественной оси х Î(-¥; +¥)