Делимость суммы, разности, произведения целых неотрицательных чисел.

Понятие отношения делимости, его свойства. Делимость суммы, разности, произведения целых неотрицательных чисел. Признаки делимости на 2, 3, 5 в десятичной системе счисления. Признак делимости на составное число.

Рассмотрим отношение делимости на множестве целых неотрицательных чисел.

Определение: Говорят, что целое неотрицательное число а делится на натуральное число b, если существует такое целое неотрицательное число q, что а=bq.

Если а делится на b, то пишут а 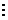b и говорят а кратно b. А называют кратным числа b, а b называют делителем числа а. Обратным к отношению «а 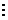b», является отношение «b делит а».

Отношение делимости является бинарным отношением на множестве целых неотрицательных чисел. Рассмотрим его свойства:

1. Отношение делимости рефлексивно, то есть .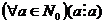
Справедливость этого свойства следует из того, что а=а•1 и 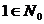. Так можно считать, что q=1.

2.Отношение делимости антисимметрично, то есть .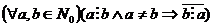
3. Отношение делимости транзитивно, то есть .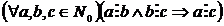
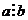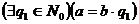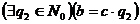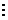действительно, поскольку , то по определению отношения делимости . Аналогично, . Тогда a=bq₁=(cq₂)q₁=c(q₁q₂) =cq, где q₁q₂=q N₀. Это означает, что а с.

Таким образом, отношение делимости на множестве N₀, обладая свойствами рефлексивности, антисимметричности и транзитивности, является отношением нестрогого порядка.

Делимость суммы, разности, произведения целых неотрицательных чисел.

Теорема: Если каждое слагаемое суммы делится на натуральное число b, то и вся сумма делится на это число, то есть .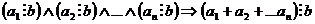

Теорема: Если каждое из чисел а и b делится на с и а≥b, то разность а-b делится на с, то есть .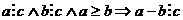

Теорема: Если хотя бы один из множителей произведения делится на натуральное число b, то и все произведение делится на это число, то есть .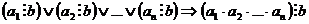

Теорема: Если в произведении ab множитель а делится на натуральное число m, а множитель b делится на натуральное число n, то произведение ab делится на произведение nm, то есть .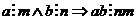

Теорема: Если в сумме одно слагаемое не делится на натуральное число b, а все остальные слагаемые делятся на это число, то и вся сумма на число b не делится.

Признак делимости на 2. Число делится на 2, если его последняя цифра - ноль или делится на 2. Числа, делящиеся на два, называются чётными, не делящиеся на два – нечётными.

Признаки делимости на 3 и 9. Число делится на 3, если его сумма цифр делится на 3. Число делится на 9, если его сумма цифр делится на 9.

Признак делимости на 5. Число делится на 5, если его последняя цифра - ноль или 5. (Подобрать примеры самостоятельно).

Рассмотрим признак делимости на составное число.

Определение: Натуральное число n≥1 называется составным, если оно имеет более двух делителей.

Определение: натуральное число р≥1 называется простым, если оно имеет только два делителя: 1 и р.

Общий признак делимости на составное число: Для того, чтобы натуральное число х делилось на составное число n = bc, где числа b и c таковы, что D(b.c) = 1(т. е. они взаимно простые), необходимо и достаточно, чтобы оно делилось на b и на c.

Например: для того, чтобы число делилось на 6, необходимо и достаточно, чтобы оно делилось на 2 и на 3.

Для того, чтобы число делилось на 60, необходимо и достаточно, чтобы оно делилось на 4, на 3 и на 5.