Лекция 5
Алгебраические выражения для аберраций третьего порядка в зависимости от конструктивных параметров оптических систем впервые были получены немецким астрономом Зейделем в 1856 году. Сразу же надо отметить, что напрямую зависимость даже аберраций третьего порядка от конструктивных параметров оптической системы (радиусы, толщины и т.д.) невозможно было получить. Зейдель использовал вспомогательный прием, использовав вместо реальных конструктивных параметров параметры первого и второго параксиальных лучей, которые однозначно связаны с реальными конструктивными параметрами. В дальнейшем для удобства применения формул Зейделя они были преобразованы для тех либо иных случаев их применения.
Для получения выражений для коэффициентов аберраций необходимо провести сложные теоретические выкладки, которые приводятся в специальной литературе, приведу только российские источники
Слюсарев Г.Г., Методы расчета оптических систем, 1937.
Слюсарев Г.Г., Методы расчета оптических систем, 1969.
Тудоровский А.И., Теория оптических приборов. Т.1, 1948.
На лекциях я приведу основную идею вывода аналитического представления аберрационных коэффициентов и основные конечные результаты.
Рассматривается угловой эйконал W для случая одной поверхности и, как нами было получено на предыдущей лекции, координаты точек пересечения луча с плоскостями предмета и изображения определяются по следующим формулам
dW/dμ’ = - n’y’
dW/ dν’ = -n’z’
dW/dμ = ny
dW/ dν = nz
Отсюда меридиональная и сагиттальная аберрации может быть записана в следующем виде
-n’δg’ = y’ –β0 y = dW/dμ’ + (n’/n) β0 dW/dμ
-n’ δG’= dW/ dν’,
где β0 = y’/y – линейное увеличение.
Весьма сложные теоретические выводы (Слюсарев, Методы расчета оптических систем, 1937 г.) позволяют получить следующие выражения для поперечных аберраций третьего порядка, вносимых одной поверхностью. Вначале отметим, что для вывода формул для аберраций Зейделя, выраженных через координаты m’, M’, l, нужно заменить направляющие косинусы лучей их выражениями через расстояние от оси до рассматриваемой точки предмета l и координатами m’, M’ пересечения луча с плоскостью выходного зрачка.
Обозначая
τ = α/α’
l/(x-s) = tgw = w
-m’/(x’-s’) = tgϭy’= ω’ (II.29)
-M’/(x’-s’) = tgϭz’= Ω’
(n’/n)βp=τ’
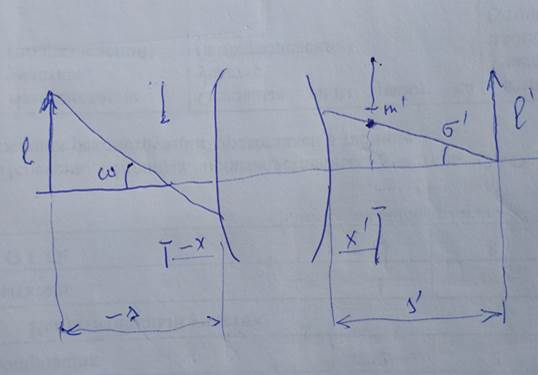
где w – угловое поле зрения,
ω’ и Ω’ – меридиональный и сагиттальный апертурные углы,
βp – линейное увеличение в зрачках,
а тангенсы улов непосредственно заменены углами, входящими в эти тангенсы, что допустимо для аберраций третьего порядка.
После целого ряда преобразований получаем окончательно для меридиональной и сагиттальной поперечной аберрации для одной поверхности следующие выражения
-2n’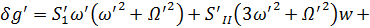 
+ 
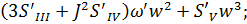(II.30)
+ 
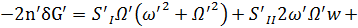
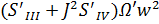
(здесь все S c тильдой)
где инвариант Лагранжа-Гельмгольца J
J=nαβ(x-s)=-nf’α’β(τ’-τ)/τ’=n’fα’β(τ’-τ)/τ’=nαl (II.30*)
~ ~ ~ ~
После ряда преобразований для коэффициентов Зейделя S’I, S’II, S’III, S’IV и S’V получены следующие выражения через параметры хода двух параксиальных лучей, один из которых пересекает оптическую ось в центре плоскости предметов и образует с осью углы α1, α2, …, αр+1 = α’p, а другой пересекает ось в центре входного зрачка и образует с осью углы β1 , β2 , …, βр+1 =βp’. Здесь р – число поверхностей оптической системы. Эти переменные введены немецким оптиком Ланге.
Рассматривая одну поверхность и используя обозначения
Мы получили выражения для отдельных аберраций третьего порядка, вносимых одной поверхностью. Следующая задача, имея аберрации отдельных поверхностей, вычислить суммарные аберрации, вносимые всей оптической системой.
Имея аберрации отдельных поверхностей, можно вычислить аберрации всей системы, перенося поперечную аберрацию, вызванную поверхностью k, в пространство изображения всей системы с помощью инварианта Лагранжа-Гельмгольца.
Пусть оптическая система имеет р поверхностей, р – номер последней поверхности системы; k – номер произвольной поверхности; тогда запишем инвариант Лагранжа-Гельмгольца
n’pα’p δg’p = n’kα’kδg’k
Для получения инварианта Лагранжа-Гельмгольца, относящегося к поверхности с номером k, достаточно помножить формулы (II.30) с обеих сторон на α’k. Складывая величины
n’kα’kδg’k,
относящиеся ко всем поверхностям, получаем поперечную аберрацию δg’p всей системы, умноженную на n’pα’p; поэтому после ряда преобразований получаем
Тогда
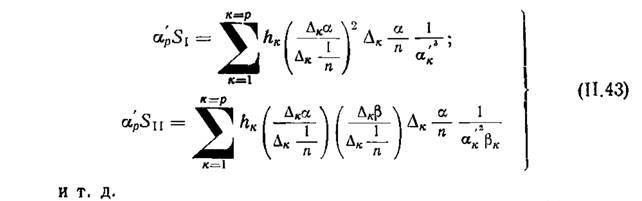
Заметим что эти выражения однородны относительно переменных α и β (в числителе и знаменателе они в одной и той же степени), то есть не зависят от выбора единиц для α и β. Поэтому нормировку параксиальных лучей удобно использовать в следующем виде
α’p = 1, β1 = 1.
Тогда выражения для коэффициентов Зейделя принимают вид
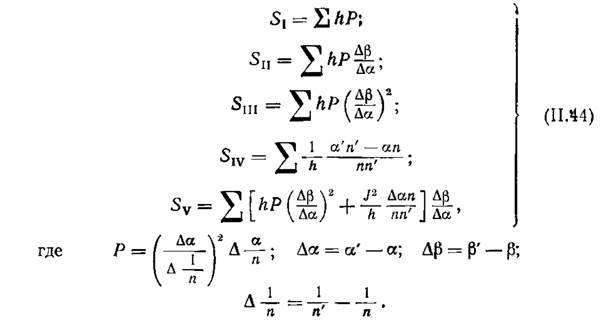
Полученные формулы относятся к общему случаю любых центрированных систем, составленных из сферических поверхностей. Из них следует, что оптическая система не имеет аберраций третьего порядка, то есть δg’ и δG’ равны нулю только в том случае, если одновременно все пять сумм Зейделя равны нулю. Естественно, это не означает, что система свободна от аберраций вообще, так как аберрации высших порядков могут иметь существенные значения. Однако, как показывает опыт расчета оптических систем, одним из условий получения системы с хорошим качеством изображения является условие получения малых аберраций третьего порядка. Однако здесь я должен сделать некоторое важное замечание. По возможности, малыми должны быть аберрации третьего порядка, вносимые каждой отдельной поверхностью, так как большие аберрации третьих порядков на некоторых поверхностях указывают на то, что эти поверхности вносят большие аберрации высших порядков.