Ряд вида
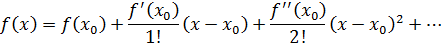
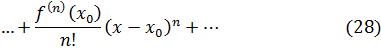
называется рядом Тейлора для функции 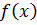 .
.
При 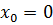 получим ряд
получим ряд
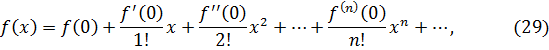
который называется рядом Маклорена.
Пусть функция 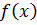 бесконечно дифференцируема в точке
бесконечно дифференцируема в точке 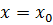 . Составим для неё формально ряд Тейлора. Для данного ряда возникают следующие вопросы:
. Составим для неё формально ряд Тейлора. Для данного ряда возникают следующие вопросы:
1. Совпадает ли сумма ряда с функцией 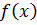 ?
?
2. При каких условиях функция 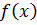 может быть разложена в ряд Тейлора?
может быть разложена в ряд Тейлора?
Найдём частичную сумму ряда Тейлора, которая называется многочленом Тейлора степени n:
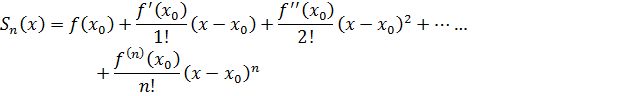
Разность между функцией 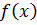 и её многочленом называется остаточным членом ряда Тейлора:
и её многочленом называется остаточным членом ряда Тейлора:
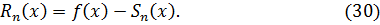
Остаточный член ряда Тейлора в форме Лагранжа имеет вид:
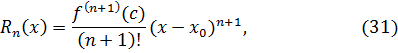
где 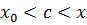 .
.
При 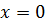 получим остаточный член ряда Маклорена:
получим остаточный член ряда Маклорена:
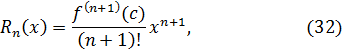
где 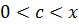 .
.
Теорема 12. Для того, чтобы бесконечно дифференцируемая в точке 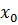 функция
функция 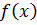 являлась суммой составленного для неё ряда Тейлора, необходимо и достаточно, чтобы остаточный член
являлась суммой составленного для неё ряда Тейлора, необходимо и достаточно, чтобы остаточный член 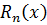 стремился к нулю при
стремился к нулю при 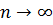 , т.е. чтобы
, т.е. чтобы 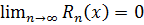 .
.
Иногда не просто определить значения х, при которых 
На практике часто пользуются следующей теоремой:
Теорема 13. (достаточное условие разложимости функции в ряд Тейлора)
Если в некоторой окрестности точки 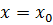 абсолютные величины всех производных функции
абсолютные величины всех производных функции 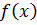 ограничены
ограничены 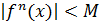 , то функция
, то функция 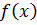 разлагается в ряд Тейлора, т.е.
разлагается в ряд Тейлора, т.е. 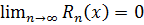 .
.
Разложение основных элементарных функций в ряд Маклорена даны в приложении 1. Используя эти разложения и формулу суммы геометрической прогрессии можно получить разложения некоторых функций в степенные ряды. В этом случае нет необходимости исследовать остаток ряда и находить отдельно интервал сходимости. При разложении функции в степенной ряд можно применять почленное дифференцирование или интегрирование степенного ряда.
Пример 29. Используя основные разложения (приложение 1), найти разложение по степеням х для функции 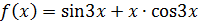 .
.
Воспользуемся разложением функций 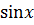 и
и 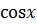 :
:
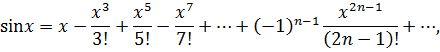
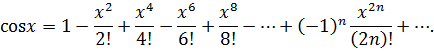
Интервал сходимости рядов: 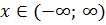 .
.
В разложениях заменим х на 3х:
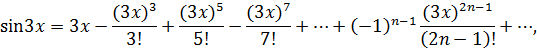
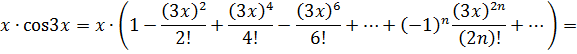
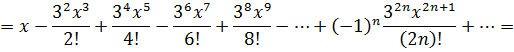
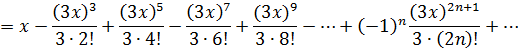
Просуммируем ряды и сгруппируем слагаемые по степеням х:
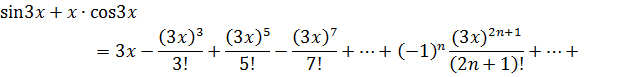
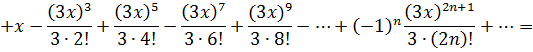
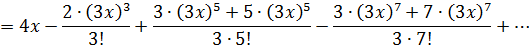
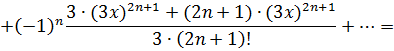

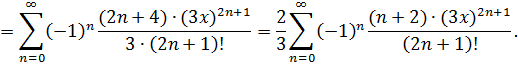
Получили разложение функции в степенной ряд:
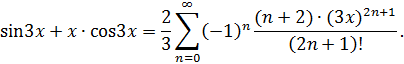
Интервал сходимости полученного ряда: 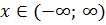 .
.
Пример 30. Разложить функцию 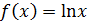 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 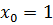 .
.
Воспользуемся рядом Тейлора:
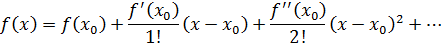
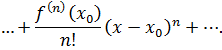
Найдём коэффициенты разложения:
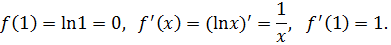

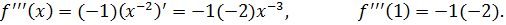
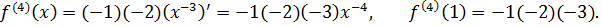
Наблюдается закономерность: 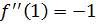 ,
, 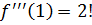 ,
, 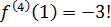 , тогда
, тогда 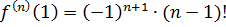 .
.
Подставим найденные значения в ряд Тейлора:
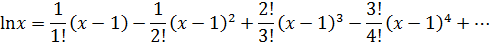
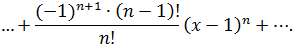
Упростив коэффициенты, получим разложение функции в ряд Тейлора:
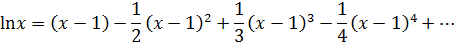
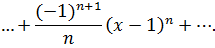
Найдём интервал сходимости полученного ряда. Общий член ряда
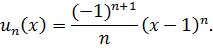
По признаку Даламбера:
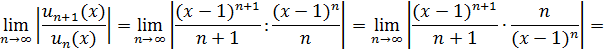
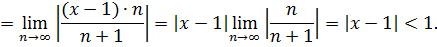
Раскроем модуль: 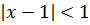 ,
, 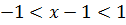 , интервал сходимости
, интервал сходимости 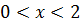 .
.
Проверим сходимость ряда на концах интервала.
При 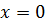 получим ряд
получим ряд 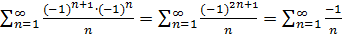 . Гармонический ряд расходится.
. Гармонический ряд расходится.
При 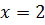 получим ряд
получим ряд 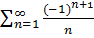 .
.
Знакопеременный числовой ряд сходится условно по признаку Лейбница.
Интервал сходимости 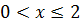 .
.
Замечание. При разложении функции в степенной ряд необходимо находить интервал сходимости.
Пример 31. Найти разложение в ряд Маклорена функции 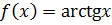 .
.
Находить разложение в степенной ряд данной функции по определению трудоёмко, так как надо вычислять производные и выявлять закономерность. Воспользуемся представлением данной функции в виде интеграла:
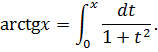
Подынтегральную функцию 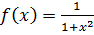 разложим в ряд Маклорена, используя разложение:
разложим в ряд Маклорена, используя разложение:
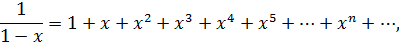
с областью сходимости 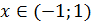 . Заменим в разложении х на
. Заменим в разложении х на 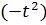 :
:
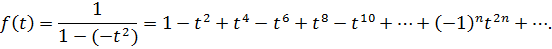
Область сходимости полученного разложения 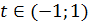 . Почленно проинтегрируем полученный ряд в пределах от 0 до х, где
. Почленно проинтегрируем полученный ряд в пределах от 0 до х, где 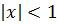 :
:
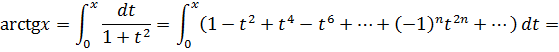
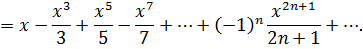
Получили разложение функции в степенной ряд:
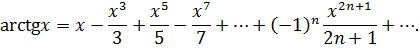
Интервал сходимости 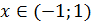 .
.
Пример 32. Представить интеграл в виде ряда по степеням х:
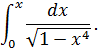
Подынтегральная функция 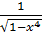 .
.
Воспользуемся частным случаем биноминального разложения функции в степенной ряд
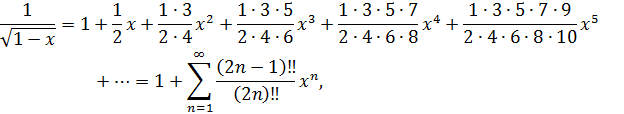
с областью сходимости 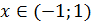 .
.
Заменим х на 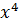 :
:
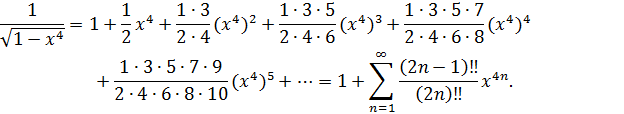
Тогда интеграл можно представить так:
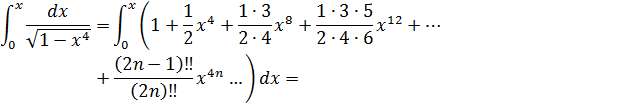
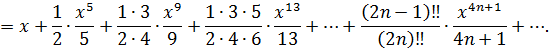
Разложение интеграла можно записать так:
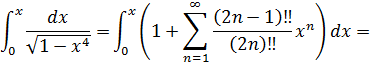
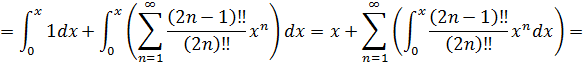
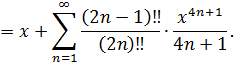
Интервал сходимости полученного ряда сохраняется: 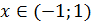 .
.
Иногда приходится решать обратную задачу: по данному разложению найти сумму ряда, или установить к какой функции ряд сходится. Для этого используют почленное дифференцирование или интегрирование степенных рядов и стандартные разложения элементарных функций (приложение 1). В каждом случае необходимо определить, какой метод применить.
Пример 32. Применяя почленное дифференцирование или интегрирование, найти сумму степенного ряда:
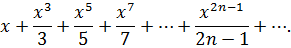
Выберем метод, который будем применять. Общий член ряда:
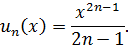
Удобно применить метод почленного дифференцирования, в этом случае сократится знаменатель 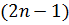 . Пусть сумма ряда равна функции
. Пусть сумма ряда равна функции 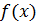 , тогда:
, тогда:
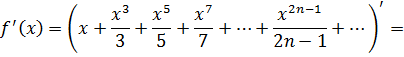
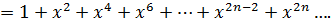
Выберем порождающий ряд из приложения (1), похожий на 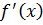 ,
,
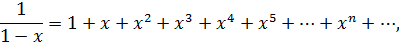
с областью сходимости 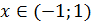 . Тогда
. Тогда
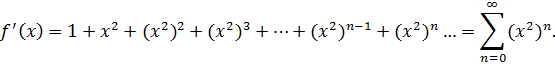
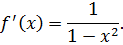
Находим:
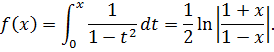
Сумма степенного ряда равна:
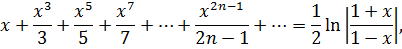
с областью сходимости 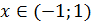 .
.
Пример 33. Применяя почленное дифференцирование или интегрирование, найти сумму ряда:
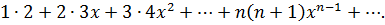
Выберем метод, который будем применять. Общий член ряда:
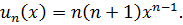
В этом примере лучше применить метод почленного интегрирования. Пусть сумма ряда равна функции 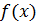 , тогда:
, тогда:
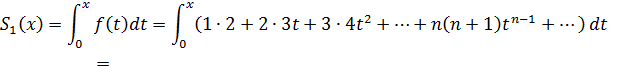
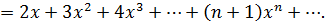
Повторно проинтегрируем:
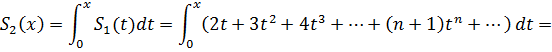
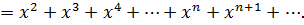
Выберем порождающий ряд из приложения (1), похожий на 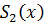
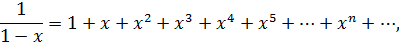
с областью сходимости 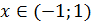 . Тогда
. Тогда
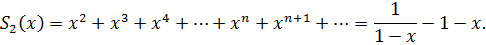
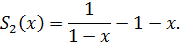
Чтобы найти функцию 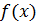 , продифференцируем полученное выражение два раза:
, продифференцируем полученное выражение два раза:
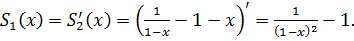
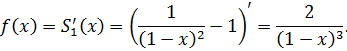
Сумма ряда равна:
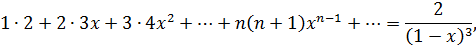
с областью сходимости 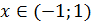 .
.
Пример 34. Разложить данную дробь в ряд по степеням х:
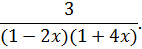
Разложим данную дробь на простейшие дроби:

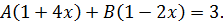
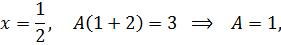
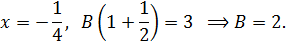
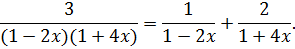
Воспользуемся разложением функции:
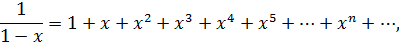
интервал сходимости 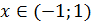 .
.
Каждую дробь разложим отдельно:
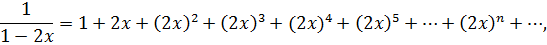
интервал сходимости, 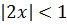 ,
, 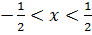 .
.
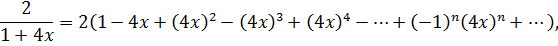
интервал сходимости, 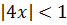 ,
, 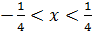 .
.
Просуммируем ряды, сгруппируем по степеням х:
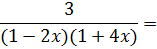
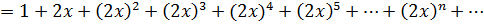
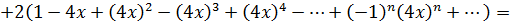
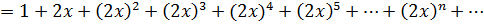
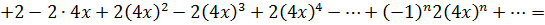
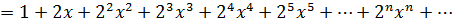
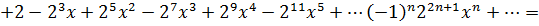
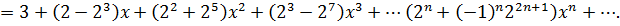
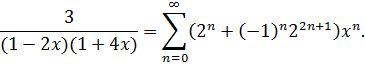
Интервал сходимости будет наименьшим из двух интервалов: 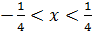 .
.