Часть 1.
Интеграл – одно из центральных понятий математического анализа и всей математики, возникновение которого связано с двумя задачами: о восстановлении функции по её производной; о вычислении площади, заключенной между графиками функции 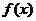 на отрезке
на отрезке  и осью абсцисс. Указанные две задачи приводят к двум видам интегралов: определённому и неопределенному.
и осью абсцисс. Указанные две задачи приводят к двум видам интегралов: определённому и неопределенному.
В ходе развития математики и под влиянием потребностей естествознания и техники понятие неопределённого интеграла и определённого интеграла подвергались ряду обобщений и изменений.
Неопределённый интеграл – совокупность всех первообразных на интервале  функции
функции 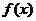 :
:  . Согласно основной теореме интегрального исчисления, для каждой непрерывной на отрезке
. Согласно основной теореме интегрального исчисления, для каждой непрерывной на отрезке  функции
функции 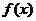 существует на соответствующем интервале первообразная и, следовательно, неопределенный интеграл. Если
существует на соответствующем интервале первообразная и, следовательно, неопределенный интеграл. Если 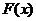 - одна из первообразных функции
- одна из первообразных функции 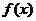 на
на 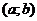 , то
, то  , где
, где 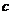 - произвольная постоянная.
- произвольная постоянная.
Следует отметить, что здесь множество значений 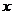 связное. На несвязном множестве неверно утверждение о том, что все первообразные непрерывной функции отличаются на константу. Так равенство
связное. На несвязном множестве неверно утверждение о том, что все первообразные непрерывной функции отличаются на константу. Так равенство  , рассматриваемое на объединении лучей
, рассматриваемое на объединении лучей  , вообще говоря, неверно. Например, на этом множестве первообразными функции
, вообще говоря, неверно. Например, на этом множестве первообразными функции 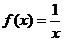 являются функции
являются функции 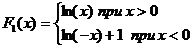 и
и 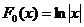 . Их разность
. Их разность  не является константой.
не является константой.
Определённый интеграл. Понятие определённого интеграла вводится как предел интегральных сумм. Для непрерывной на отрезке 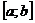 функции
функции 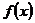 понятие определённого интеграла впервые было введено Коши в его работе 1823 года:
понятие определённого интеграла впервые было введено Коши в его работе 1823 года:  для разбиений
для разбиений  . Это частный случай определённого интеграла Римана (1853г.). Существенное продвижение в теории определённого интеграла принадлежит Дарбу, который ввёл наряду с интегральной суммой Римана верхнюю и нижнюю суммы (1879г.). Необходимое и достаточное условие интегрируемости по Риману разрывных функций установлено в 1902г. Лебегом.
. Это частный случай определённого интеграла Римана (1853г.). Существенное продвижение в теории определённого интеграла принадлежит Дарбу, который ввёл наряду с интегральной суммой Римана верхнюю и нижнюю суммы (1879г.). Необходимое и достаточное условие интегрируемости по Риману разрывных функций установлено в 1902г. Лебегом.
Между определённым интегралом от непрерывной на отрезке 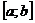 функции и неопределённым интегралом (то есть первообразной) этой функции существует следующая связь:
функции и неопределённым интегралом (то есть первообразной) этой функции существует следующая связь:
1) Если 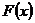 - любая первообразная функции
- любая первообразная функции 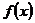 , то справедлива формула Ньютона-Лейбница:
, то справедлива формула Ньютона-Лейбница:
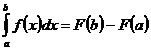 ;
;
2) Для любого  неопределённый интеграл непрерывной функции
неопределённый интеграл непрерывной функции 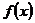 записывается в виде:
записывается в виде:

где 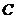 – произвольная постоянная. В частности, определённый интеграл с переменным верхним пределом
– произвольная постоянная. В частности, определённый интеграл с переменным верхним пределом  представляет собой первообразную функцию
представляет собой первообразную функцию 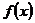 .
.
Определённый интеграл Лебега. Для введения определённого интеграла от функции 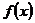 в смысле Лебега разбивают множество значений
в смысле Лебега разбивают множество значений 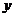 на частичные отрезки точками
на частичные отрезки точками  и обозначают через
и обозначают через  множество всех значений
множество всех значений  , для которых
, для которых 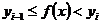 , а через
, а через 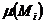 – меру множества
– меру множества  в смысле Лебега. Интегральную сумму Лебега функции
в смысле Лебега. Интегральную сумму Лебега функции 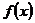 на отрезке
на отрезке 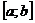 определяют равенством
определяют равенством 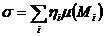 , где
, где 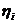 – любое число из отрезка
– любое число из отрезка 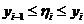 .
.
Функцию 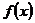 называют интегрируемой в смысле Лебега на отрезке
называют интегрируемой в смысле Лебега на отрезке 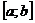 , если существует предел её интегральных сумм при стремлении к нулю
, если существует предел её интегральных сумм при стремлении к нулю  . То есть если существует такое число
. То есть если существует такое число 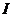 , что для любого
, что для любого  найдется
найдется 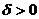 такое, что при единственном условии
такое, что при единственном условии 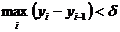 справедливо неравенство
справедливо неравенство 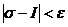 . При этом указанный предел
. При этом указанный предел 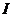 называют определённым интегралом Лебега от функции
называют определённым интегралом Лебега от функции 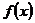 по отрезку
по отрезку 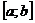 .
.
Вместо отрезка 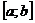 логично рассматривать произвольное множество, измеримое относительно некоторой неотрицательной полной счётно-аддитивной меры. Возможно и другое определение интеграла Лебега, когда этот интеграл первоначально определяют на множестве так называемых простых функций (то есть измеримых функций, принимающих не более счётного множества значений), а затем с помощью операции предельного перехода расширяют понятие интеграла для произвольной функции, представляющей собой предел равномерно сходящейся последовательности простых функций (равномерной сходимости достаточно почти всюду).
логично рассматривать произвольное множество, измеримое относительно некоторой неотрицательной полной счётно-аддитивной меры. Возможно и другое определение интеграла Лебега, когда этот интеграл первоначально определяют на множестве так называемых простых функций (то есть измеримых функций, принимающих не более счётного множества значений), а затем с помощью операции предельного перехода расширяют понятие интеграла для произвольной функции, представляющей собой предел равномерно сходящейся последовательности простых функций (равномерной сходимости достаточно почти всюду).
Каждая интегрируемая в смысле Римана функция ограничена и интегрируема в смысле Лебега. Обратное утверждение неверно, ибо существуют разрывные на множестве положительной меры и вместе с тем ограниченные интегрируемые в смысле Лебега функции (например, функция Дирихле.) Для интегрируемости по Лебегу ограниченной функции необходимо и достаточно, чтобы эта функция принадлежала классу измеримых функций. Функции, встречающиеся в математическом анализе, как правило, измеримы. Это означает, что интеграл Лебега обладает общностью, исчерпывающей потребности анализа.
Интеграл Лебега охватывает и все случаи абсолютно сходящихся несобственных интегралов.
Несобственный интеграл – интеграл от неограниченной функции или от функции по неограниченному множеству. Пусть функция 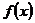 определена на конечном или бесконечном полуинтервале
определена на конечном или бесконечном полуинтервале  ,
,  , и для любого
, и для любого  , функция
, функция 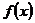 интегрируема по Риману (по Лебегу) на отрезке
интегрируема по Риману (по Лебегу) на отрезке  . Несобственным интегралом называют
. Несобственным интегралом называют
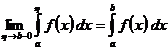
(в случае 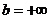 условие
условие 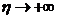 ). Если предел существует, то говорят, что несобственный интеграл сходится, если не существует – расходится. Например, несобственный интеграл:
). Если предел существует, то говорят, что несобственный интеграл сходится, если не существует – расходится. Например, несобственный интеграл:
 ,
,  ,
,
сходится при  , а при
, а при 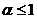 расходится. Если же
расходится. Если же 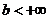 , то
, то 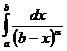 сходится при
сходится при 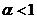 и расходится при
и расходится при  .
.
Если 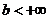 и функция
и функция 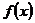 интегрируема по Риману (по Лебегу) на отрезке
интегрируема по Риману (по Лебегу) на отрезке 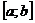 , то несобственный интеграл совпадёт с определённым интегралом. Аналогично при соответствующих предположениях определяют несобственный интеграл по промежутку
, то несобственный интеграл совпадёт с определённым интегралом. Аналогично при соответствующих предположениях определяют несобственный интеграл по промежутку 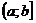 ,
, 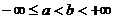 :
: 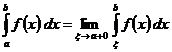 .
.
Если функция  интегрируема по Риману (по Лебегу) на каждом отрезке
интегрируема по Риману (по Лебегу) на каждом отрезке  ,
, 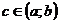 и существуют несобственные интегралы
и существуют несобственные интегралы  и
и  , то существует несобственный интеграл
, то существует несобственный интеграл 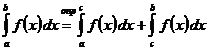 и он не зависит от выбора точки
и он не зависит от выбора точки 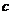 .
.
Например, 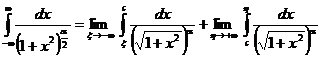 сходится при любых
сходится при любых  и расходится при
и расходится при  .
.
Если на интервале 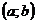 имеется конечное число точек
имеется конечное число точек 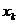 ,
,  ,
,  таких, что функция
таких, что функция  интегрируема по Риману (по Лебегу) на каждом отрезке
интегрируема по Риману (по Лебегу) на каждом отрезке 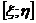 , не содержащем ни одной точки
, не содержащем ни одной точки 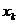 , и для каждого
, и для каждого 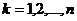 , существует несобственный интеграл
, существует несобственный интеграл 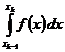 , то несобственный интеграл
, то несобственный интеграл 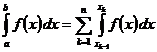 . Это определение не зависит от выбора точек
. Это определение не зависит от выбора точек 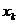 .
.
На несобственные интегралы переносятся общие свойства интегралов: линейность, аддитивность относительно промежутков, по которым производится интегрирование, правило интегрирования неравенств, теоремы о среднем, интегрирование по частям и замены переменного, формула Ньютона-Лейбница. Например, если функция 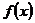 почти всюду на
почти всюду на  совпадает с производной функции
совпадает с производной функции  , которая абсолютно непрерывна на каждом отрезке
, которая абсолютно непрерывна на каждом отрезке  ,
, 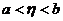 ,то
,то  . Конкретный пример:
. Конкретный пример: 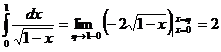 .
.
Для выяснения сходимости несобственного интеграла от знакопостоянных функций применяется признак сравнения. Например, известно, что 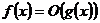 при
при  ,
, 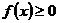 ,
, 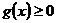 ,
, 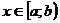 , тогда из сходимости несобственного интеграла
, тогда из сходимости несобственного интеграла 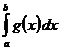 следует сходимость несобственного интеграла
следует сходимость несобственного интеграла  . Функция
. Функция  называется в этом случае функцией сравнения. В качестве функции сравнения часто используется степенная функция, что продемонстрировано в приведённых примерах.
называется в этом случае функцией сравнения. В качестве функции сравнения часто используется степенная функция, что продемонстрировано в приведённых примерах.
Необходимое и достаточное условие сходимости несобственного интеграла даёт критерий Коши. Так, несобственный интеграл на  сходится тогда и только тогда, когда для любого
сходится тогда и только тогда, когда для любого  существует такое
существует такое  , что для всех
, что для всех 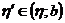 ,
,  выполняется неравенство
выполняется неравенство  .
.
Несобственный интеграл  называется абсолютно сходящимся, если сходится несобственный интеграл
называется абсолютно сходящимся, если сходится несобственный интеграл  .
.
Если несобственный интеграл абсолютно сходится, то он сходится и совпадает с интегралом Лебега. Существуют несобственные интегралы сходящиеся, но не абсолютно сходящиеся. Например, для конечного промежутка несобственный интеграл 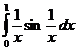 , а для бесконечного
, а для бесконечного  .
.
Существуют различные признаки сходимости несобственного интеграла.  Например, если на полуоси
Например, если на полуоси 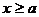 функция
функция 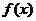 имеет ограниченную первообразную, а
имеет ограниченную первообразную, а 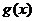 – монотонная функция, стремящаяся к нулю при
– монотонная функция, стремящаяся к нулю при  , то интеграл
, то интеграл 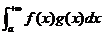 сходится. Другой признак: если несобственный интеграл
сходится. Другой признак: если несобственный интеграл 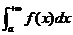 сходится, а функция
сходится, а функция 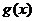 монотонна и ограничена при
монотонна и ограничена при 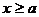 , то несобственный интеграл
, то несобственный интеграл 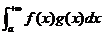 сходится.
сходится.
Сходимость несобственного интеграла можно выразить в терминах сходящихся рядов. Например, для того, чтобы несобственный интеграл по 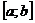 сходился, необходимо и достаточно, чтобы для любой последовательности
сходился, необходимо и достаточно, чтобы для любой последовательности 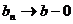 ,
,  сходился ряд
сходился ряд 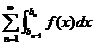 , причем в случае сходимости ряда его сумма совпадает с несобственным интегралом.
, причем в случае сходимости ряда его сумма совпадает с несобственным интегралом.
Понятие несобственного интеграла обобщается для функций многих переменных.
Определение. Функция 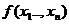 , определенная на открытом (ограниченном или неограниченном) множестве
, определенная на открытом (ограниченном или неограниченном) множестве  называется интегрируемой в несобственном смысле по множеству
называется интегрируемой в несобственном смысле по множеству 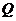 , если для любой последовательности измеримых по Жордану множеств
, если для любой последовательности измеримых по Жордану множеств 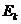 таких, что
таких, что 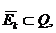
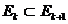 ,
, 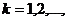
 , существует
, существует 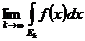 , не зависящий от выбора указанной последовательности. Этот предел, если он существует, называется несобственным интегралом
, не зависящий от выбора указанной последовательности. Этот предел, если он существует, называется несобственным интегралом 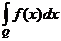 . При
. При 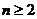 он существует тогда и только тогда, когда существует несобственный интеграл
он существует тогда и только тогда, когда существует несобственный интеграл  .
.
Итак, в отличие от одномерного случая в многомерной области функция интегрируема в несобственном смысле тогда и только тогда, когда она абсолютно несобственно интегрируема. То есть в многомерном случае интеграл Римана, понимаемый в определенном смысле или несобственном смысле, является интегралом Лебега.
В приложениях часто возникают повторные интегралы. Связь между кратными и повторными интегралами Лебега устанавливает
Теорема Фубини. Пусть  ограниченная n-мерная область переменных
ограниченная n-мерная область переменных 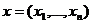 , а
, а  ограниченная m-мерная область переменных
ограниченная m-мерная область переменных 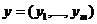 , в ограниченной области
, в ограниченной области 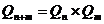 (n+m)-мерного пространства переменных (x,y) задана функция f(x,y). Если функцияf(x,y) интегрируема по
(n+m)-мерного пространства переменных (x,y) задана функция f(x,y). Если функцияf(x,y) интегрируема по 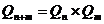 , то f(x,y) для почти всех
, то f(x,y) для почти всех 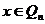 интегрируема по
интегрируема по  , для почти всех
, для почти всех  f(x,y) интегрируема по
f(x,y) интегрируема по 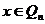 , функции
, функции  и
и 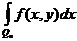 интегрируемы по
интегрируемы по 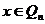 и по
и по  соответственно и
соответственно и
 .
.
Отметим, что из существования повторных интегралов, вообще говоря, не следует их равенство и существование двойного интеграла. На практике обычно пользуются следствием теоремы Фубини: если функция f(x,y) неотрицательна, то из существования хотя бы одного повторного интеграла следует существование двойного: 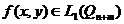 , а тогда справедлива теорема Фубини, то есть существует второй повторный интеграл и выполнено равенство всех трех интегралов.
, а тогда справедлива теорема Фубини, то есть существует второй повторный интеграл и выполнено равенство всех трех интегралов.
К несобственным интегралам относятся интегралы в смысле главного значения.
Определение. Пусть функция 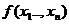 определена на открытом множестве
определена на открытом множестве 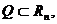
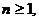 кроме, может быть, точки
кроме, может быть, точки 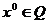 , и пусть для любого
, и пусть для любого  функция
функция  интегрируема по Риману или по Лебегу на множестве
интегрируема по Риману или по Лебегу на множестве 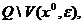 где
где  - шар радиуса
- шар радиуса 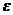 с центром
с центром  . Тогда, если существует
. Тогда, если существует  , то его называют интегралом в смысле главного значения и обозначают
, то его называют интегралом в смысле главного значения и обозначают 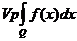 .
.
Если существует несобственный интеграл 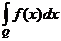 , то он существует и в смысле главного значения. Обратное, вообще говоря, неверно. Например, несобственный интеграл
, то он существует и в смысле главного значения. Обратное, вообще говоря, неверно. Например, несобственный интеграл  расходится, а
расходится, а  . Аналогично определяется интеграл в смысле главного значения в бесконечности:
. Аналогично определяется интеграл в смысле главного значения в бесконечности: 
Общность, достигнутая определением интеграла в смысле Лебега, весьма существенна во многих вопросах современного математического анализа: теория обобщенных функций, определение обобщенных решений дифференциальных уравнений, изоморфизм гильбертовых пространств 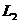 и
и  . Все эти теории оказались возможными только при понимании интеграла в смысле Лебега.
. Все эти теории оказались возможными только при понимании интеграла в смысле Лебега.
Первообразную в смысле Лебега определяют равенством  , в котором интеграл понимается в смысле Лебега. При таком понимании равенство
, в котором интеграл понимается в смысле Лебега. При таком понимании равенство  будет справедливо почти всюду. В частности, это равенство выполнено во всех точках непрерывности функции
будет справедливо почти всюду. В частности, это равенство выполнено во всех точках непрерывности функции  .
.
Понятие неопределенного, определенного интегралов и интеграла в смысле главного значения переносятся на случай функций комплексного переменного.