Наиболее вероятное число успехов в серии повторных независимых испытаний – это такое число 
, при котором биномиальная вероятность 
является наибольшей для данного числа испытаний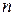 
.
Таким образом, вероятность является наибольшей среди вероятностей 
, 
, …, 
, …, 
.
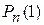Наиболее вероятное число успехов удовлетворяет неравенству
, или 
.
Отметим, что - целое число и может быть не единственным.
Пример 5. Найти наивероятнейшее число годных деталей среди 19 проверяемых, если вероятность детали быть годной, равна 0,9.
По условию задачи 
, 
, 
. Найдем целое число , удовлетворяющее неравенству: 
, или 
, или 
.
Это означает, что вероятности 
и 
- наибольшие среди всех биномиальных вероятностей 
при 
.
Наивероятнейшее число годных деталей равно 17 или 18. Другими словами, при заданных условиях среди 19 проверяемых деталей вероятнее всего будет 17 или 18 годных деталей.
Локальная теорема Муавра-Лапласа
2.1. Вычисление при больших 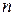и не малых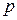 
Теорема. При больших значениях 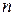и не малых 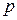вероятность 
появления события 
раз в схеме из 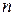независимых испытаний Бернулли приближенно вычисляется по формуле 
, где вспомогательная величина 
.
Функция 
называется малой функцией Лапласа. Ее значения приведены в таблице (Приложение 1).
Пример 6. Найти вероятность того, что при 100 подбрасываниях монеты герб появится ровно 50 раз.
Событие - появление герба при одном подбрасывании монеты, 
. По условию задачи 
. Так как число испытаний достаточно велико, то искомую вероятность 
найдем по приближенной формуле Муавра-Лапласа:
.
Значение 
найдено по таблице в Приложении.
2.2. Свойства и график функции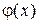 
-5 0 5 
График функции 
Свойства функции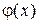
|
|
§ Функция 
четная: 
. Значит, ее график симметричен относительно оси ординат.
§ Функция принимает только положительные значения. Значит, ее график выше оси абсцисс.
§ Если значения аргумента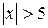 
, то значение функции 
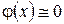. Поэтому в таблице приведены значения функции только для значений аргумента от 0 до 5.
Интегральная теорема Муавра-Лапласа
3.1. Вычисление 
при больших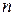
Теорема. При большом числе независимых испытаний 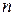вероятность появления события от 
до 
раз приближенно вычисляется по интегральной формуле Муавра-Лапласа 
, где 
и 
.
Функция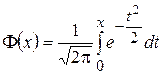 
называется функцией Лапласа, еезначения приведены в таблице (Приложение 2).
3.2. Свойства и график функции Лапласа 
0,5
-5 0 5
-0,5
График функции Лапласа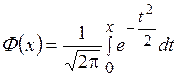 
Свойства функции Лапласа
§ 
, значит, график проходит через начало координат.
§ 
- нечетная функция, значит, график симметричен относительно начала координат.
§ 
, значит, прямые 
и 
являются горизонтальными асимптотами. При 
полагают 
, а при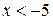 
полагают 
Пример 7. Найти вероятность того, что при 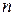= 100 подбрасываниях монеты герб появится от 
= 40 до = 60 раз.
Вероятность 
найдем, применяя приближенную формулу Муавра Лапласа.
Здесь: 
; 
;
; 
.
По формуле получим:
Здесь использовано свойство нечетности функции Лапласа . Значение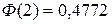 
найдено по таблице.
Теорема Пуассона
Теорема. Если число испытаний 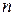велико, а вероятность появления события 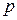в каждом испытании мала ( 
), то для вычисления вероятности применяют приближенную формулу Пуассона 
, где - число появлений события в 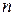независимых испытаниях; 
- среднее число появления события в 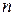испытаниях. Значения функции Пуассона 
приведены в таблице (Приложение 3).
|
|
Пример 8. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность того, что в течение часа позвонят на станцию только один абонент.
Вероятность 
того, что абонент дозвонится в течение часа (успех) мала, 
. Число одинаковых испытаний (звонки абонентов) велико 
.
Для нахождения вероятности 
применим теорему Пуассона. Найдем значение 
, тогда вероятность 
.
Контрольные вопросы
1. Опишите схему независимых испытаний Бернулли. Приведите пример.
2. Можно ли считать схемой Бернулли многократное бросание кубика?
3. Вероятность какого события обозначается ?
4. Как можно найти вероятность : 1) при небольшом числе испытаний; 2) при большом числе испытаний?
5. Почему сумма всех биномиальных вероятностей равна 1?
6. Вероятность какого события обозначается 
? Как можно найти эту вероятность: 1) при небольшом числе испытаний; 2) при большом числе испытаний?
7. Как в последовательности независимых испытаний найти вероятности: 1) только одного успеха; 2) хотя бы одного успеха; 3) полного успеха; 4) полной неудачи?
8. Что понимается под наиболее вероятным числом успехов? Как найти это число?
9. При каких условиях применима локальная теорема Лапласа?
10. Запишите функцию Лапласа и сформулируйте ее свойства.
11. При каких условиях применима интегральная теорема Муавра-Лапласа?
12. Как находится параметр в локальной формуле Лапласа?
|
|
13. При каких условиях применима формула Пуассона? Приведите пример.
14. Как находится параметр 
для формулы Пуассона?