Алгоритм блочного-QMR - это итерационный алгоритм для решения систем уравнений с несколькими правыми частями. Комплексная симметричная версия с правым предварительным условием приведена в алгоритме 4.4. Задача  X=B решена, где матрицы Z и M комплексно-симметричны.
X=B решена, где матрицы Z и M комплексно-симметричны.
Идея комплексного симметричного алгоритма блочного-QMR состоит в том, чтобы вычислить новые векторы вида  , где
, где  = [
= [ 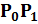 ...
... 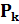 ] происходит из алгоритма 4.2 и
] происходит из алгоритма 4.2 и  =
=  .
.
LU-разложение  используется для генерации модернизированной формулы для
используется для генерации модернизированной формулы для 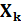 . Модернизированная формула находит минимальную невзку. Из-за того, что
. Модернизированная формула находит минимальную невзку. Из-за того, что  и
и 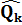 биортогональны, а не ортогональны, минимум является квази-минимумом. Следовательно, название метода, метод блочных-квази-минимальных невязок. Невязка вычисляется по Теореме 4.4.1.
биортогональны, а не ортогональны, минимум является квази-минимумом. Следовательно, название метода, метод блочных-квази-минимальных невязок. Невязка вычисляется по Теореме 4.4.1.
Теорема 4.4.1. Пусть  , где
, где 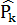 = [
= [ 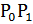 ...
...  ]. Здесь
]. Здесь 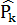 определяется по алгоритму 4.2. Тогда невязка
определяется по алгоритму 4.2. Тогда невязка  = B -
= B -  определяется как
определяется как  =
= 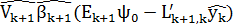 где
где  = [
= [  0... 0] T и структура
0... 0] T и структура 
Алгоритм 4. Алгоритм Block-QMR для нескольких правых частей.
Require B, X, Z, M
Ensure X  B
B

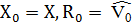

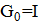
[  ,
, 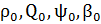 ]=gram_M_sym(
]=gram_M_sym(
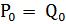

 : maxiter do
: maxiter do
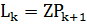
 =
= 


[  ,
, 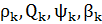 ]=gram_M_sym(
]=gram_M_sym(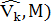

 =
= 
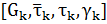 = given
= given 
if convergence is achieved then
X= 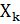
Break
end if

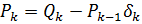

Доказательство из алгоритма невязка определяется как
Rk = B − ZXk = B − ZX – 
= 
= 
= 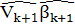 (
( )
)
= 
что доказывает теорему.
Обратите внимание, что ||  ||
||  . Поскольку с первой частью этого выражения ничего не поделаешь,
. Поскольку с первой частью этого выражения ничего не поделаешь, 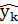 выбирается так, чтобы минимизировать
выбирается так, чтобы минимизировать  . Если
. Если  =
=  то
то  . Отсюда, используя процедуру описанную в [20, 39], получается простая модернизированная формула вида
. Отсюда, используя процедуру описанную в [20, 39], получается простая модернизированная формула вида  . Можно также найти аналогичную модернизированную формулу для невязки
. Можно также найти аналогичную модернизированную формулу для невязки  , определяемого как
, определяемого как  =
= 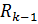 −
− 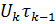 .
.
Подход, используемый для метода блочных-квази-минимальных невязок, сначала находит подходящий алгоритм Ланцоша. Алгоритм Ланцоша генерирует блочную трехдиагональную матрицу, из которой можно вычислить LU-разложение. Нижнетреугольная матрица LU-разложения затем используется для нахождения простой задачи минимизации. Задача минимизации решается с помощью QR-разложения, которую можно модернизировать по формуле рекурсии(?). Таким образом вычисляется приближенное решение Xk.
4. Block-BCG. Матричная полиномиальная интерпретация алгоритма блочного BCG.
2.1. Алгоритм блочного BCG. Алгоритм блочно-бисопряженных градиентов (Bl-BCG) был впервые предложен О'Лири [15] для решения линейных систем. Этот алгоритм является обобщением известного алгоритма BCG [6]. Bl-BCG вычисляет два набора матриц направлений { 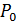 ,…
,…  } и {
} и { 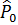 ,…
,…  } которые охватывают блочное крыловское подпространство
} которые охватывают блочное крыловское подпространство  и
и  , где
, где  = B -A
= B -A  и
и 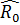 - произвольная матрица размерности N * s. Алгоритм можно представить следующим образом
- произвольная матрица размерности N * s. Алгоритм можно представить следующим образом
Алгоритм 3: Блок BCG
1.  предполагаемая матрица размерности N×s,
предполагаемая матрица размерности N×s,  = B -A
= B -A 
2. 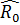 произвольная матрица размерности N×s
произвольная матрица размерности N×s
3. 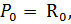

4. Для k=0,1,… вычислить
5. 
6. 
7. 
8. 
9. 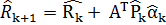
10. 
11. 
12. 
13. 
14. end
Алгоритм прерывается, если матрицы единичные. Отметим также, что коэффициенты матрицы, вычисленные в алгоритме, являются решениями линейных систем размерности sxs. Матрицы этих систем могут быть очень плохо обусловлены, и это повлияет на итерации, вычисленные методом Bl-BCG.
Bl-BCG также может демонстрировать неравномерное поведение норм невязки. Чтобы решить эту проблему, можно использовать метод блочного сглаживания [11] или процедуру блочной квази-минимизации (см. [7] и [20]).
Невязки матрицы и направления матрицы, генерируемые ALGORITHM 1, удовлетворяют нижеследующим свойствам.
Теорема 1. [15] Если не происходит разбивки, матрицы, вычисленные по алгоритму Bl-BCG, удовлетворяют следующим свойствам:
1) 
2) 
3) 
4)  и все столбцы
и все столбцы  ортогональны
ортогональны 
С этого момента мы предполагаем, что в алгоритме Bl-BCG не происходит сбоев. В следующем подразделе мы используем матричные многочлены, чтобы дать новое выражение для итераций, вычисленных Bl-BCG. Это позволит нам определить блочный алгоритм BiCGSTAB.
Собрав все эти соотношения, алгоритм Bl-BiCGSTAB можно обобщить следующим образом
АЛГОРИТМ 3: Bl-BiCGSTAB
1.  an initial gues;
an initial gues; 
2. 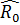 an arbitrary Nxs matrix
an arbitrary Nxs matrix
3. For k=0,1,2… compute
4. 
5. 
6. 
7. 
8. 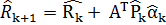
9. 
10. 
12. 
13. 
14. end
Обратите внимание, что когда решается одна линейная система, ALGORITHM 3 сводится к BiCGSTAB. Однако коэффициент Bk, вычисленный по алгоритму 3 с s = 1, определяется как Bk = - [R0, Tk] 2 / [R0, Vk] 2. Это выражение для Bk проще, чем приведенное в ALGORITHM 2, но требует дополнительного внутреннего произведения.
Алгоритм Bl-BiCGSTAB также будет прерван, если R0Vk является единичной матрицей. В ситуациях, когда матрица R0Vk неединичная, но очень плохо обусловлена, вычисление итераций также будет затронуто. Чтобы преодолеть эти проблемы, можно перезапустить с другим R0.
Благодаря локальным этапам минимизации нормы Фробениуса, Bl-BiCGSTAB имеет более плавную сходимость, чем Bl-BCG. Тем не менее, нормы невязки, полученных BlBiCGSTAB, могут колебаться в некоторых случаях. В этом случае мы можем использовать метод блочного сглаживания, определенную в [11], чтобы получить нерастущие Фробениусовские нормы невязок.
Для решения линейной системы (1.1) Bl-BiCGSTAB требует для каждой итерации вычисления 2s матрично-векторных произведений A и общим произведением 6Ns ^ 2 + 4Ns + O (s ^ 3). Это нужно сравнить с s матрично-векторным произведением A, s матрично-векторным произведением At и в общей сложности 8Ns ^ 2 + O (s ^ 3) умножений, необходимых на каждой итерации для Bl-BCG.
Требования к памяти (исключая требования A, X и B) и основные вычислительные затраты (умножения) на итерацию для алгоритмов Bl-BCG и Bl-BiCGSTAB перечислены в таблице 1.
Таблица 1. Требования к памяти и вычислительные затраты (умножения) для Bl-BCG и Bl-BiCGSTAB
| Costs | Bl-BCG | Bl-BCGSTAB |
| Mat-Vec with A | s | 2s |
Mat-Vec with 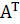
| s | - |
| Multiplications | 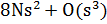
| 
|
| Memory locations | 
| 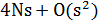
|
Затраты Bl-BCG и Bl-BiCGSTAB быстро увеличивается с увеличением числа правых сторон. Однако эти блочные методы решения сходятся за меньшее число итераций, чем их аналоги по единичного решения правых частей, поскольку размерность пространств поиска увеличиваются на Kk (A, R0) и K2k (A, R0) и равны с и 2с соответственно на каждом шаге.
Как показано в таблице 2, Bl-BiCGSTAB находит решение СЛАУ точнее, чем Bl-GMRES или BiCGSTAB, применяемый для отдельной каждой правойчасти линейной системы.
Относительная плотность матриц и использование предобуславливания делают блочные методы менее затратными, а потому они более эффективны.
Таблица 2. Эффективность Bl-BiCGSTAB по сравнению с Bl-GMRES и BiCGSTAB с использованием предобуславливания ILUT.
| Matrix | s=5 | s=10 | s=5 | s=10 |
| Utm 1700a (N=1700) (nnz(A)=21313 | 
| 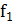 (10)=0.38 (10)=0.38
|  =0.62 =0.62
|  (10)=0.36 (10)=0.36
|
| SAYLR4(N=3564) (nnz(A)=22316) |  0.77 0.77
| 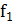 (10)=0.89 (10)=0.89
|  =0.06 =0.06
|  (10)=0.12 (10)=0.12
|
| SHERMAN5(3312) (nnz(A)=20793) |  0.93 0.93
| 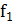 (10)=0.94 (10)=0.94
|  =0.26 =0.26
|  (10)=0.16 (10)=0.16
|
| SHERMAN3(N=5005) (nnz(A)=20033) |  0.82 0.82
| 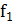 (10)=1.10 (10)=1.10
|  =0.27 =0.27
|  (10)=0.25 (10)=0.25
|
Выводы по работе
Проще говоря блочные методы важны для приложений, в которых возникают линейные системы с многими правыми частями. Однако с теоретической точки зрения они исследованы не слишком хорошо. Помимо их привлекательности при решении линейных систем с несколькими правыми частями, есть и другие аргументы в их пользу: они помогают снизить отрицательный эффект существенно последовательной операции скалярного произведения в параллельных вычислительных средах, а так же уменьшить стоимость обменов между разными уровнями памяти при реализациях использующих внешнюю память.
Список использованных источников
1. Ю.Саад Итерационные методы для разряженных линейных систем. 2013. – 171с.
2. Электромагнитная совместимость: вычислительные методы / С.П.Куксенко // Томск: Томск. гос. ун-т систем упр. и радиоэлектроники, 2018. – 215 с.
3. Итерационные методы решения СЛАУ с плотной матрицей / С.П.Куксенко. Т.Р.Газизов.
4. K. JBILOU, Smoothing iterative block methods for linear systems with multiple right-hand sides, J. Comput. Appl. Math., 107(1999), pp. 97-109
5. D. O’LEARY, The block conjugate gradient algorithm and related methods, Linear Algebra Appl., 29(1980), pp. 293-322
6. R. FLETCHER, Conjugate gradient methods for indefinite systems, In G. A. Watson, editor, Proceedings of the Dundee Biennal Conference on Numerical Analysis 1974, pages 73- Iterative Solution of Maxwell’s Equations in Frequency Domain
7. Iterative Solution of Maxwell’s Equations in Frequency Domain / MARTIN NILSSON / New York, 1975
8. Методы решения СЛАУ большой размерности / М.Ю.Баландин Э.П.Шурина 1 августа 2000 г.