Неопределенный интеграл и его основные свойства
Пусть F(x) такова, что F¢(x) = f(x) и dF(x) = f(x)dx. Тогда F(x) – первообразная для f(x), а F(x) + C – всё множество первообразных для f(x).
óнеопределенный интеграл f(x)dx.
= F(x) + C ó d(F(x) + C) = f(x)dx или (F(x) + C)¢ = f(x)
Свойства неопределенного интеграла:
1. 
= k 
2. 
= 
3. d =
4. 
= F(x) + C
5. ()¢ = f(x)
Основные свойства определённого интеграла
1. 
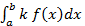= k 
2. 
= 
3. = 
4. 
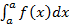= 0
5. = 
+ 
Формула Ньютона – Лейбница
= F(b) – F(a)
Определенный интеграл от a до b 
это изменение любой первообразной для f(x) при изменеии аргумента от a до b. (F(x))¢ = f(x), т.е. F(x) + C - все первообразные для f(x).
Основные законы комбинаторики
Комбинаторика – это раздел математики, в котором изучаются вопросы о том, какие комбинации можно составить из элементов какого-либо множества и сколько сколько комбинаций с теми или иными свойствами можно составить.
Правило суммы (a или b = m+n). Если эл-т а можно выбрать m способами, эл-т b можно выбрать n способами, причем любой выбор эл-та а отличен от выбора эл-та b, то а или b можно выбрать m+n способами.
Правило произведения (а или b = m 
n). Если эл-т а можно выбрать m способами, а после каждого такого выбора независимо от него эл-т b можно выбрать n способами/, то парой a и b можно выбрать m n способами.
Основные формулы комбинаторики
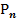= n!
= 
= 
= 
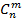Перестановки, сочетания и размещения без повторений
Перестановками из n эл-тов называются такие комбинации, каждая из которых содержит все n-элементов и которые отличаются только порядком расположения эл-тов.
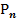- количество перестановок из n эл-тов.
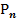= n!
Размещениями из n эл-тов по m (m ≤ n) эл-тов, называются такие комбинации, в каждой из которых содержится m эл-тов, взятых из числа данных n эл-тов и которые отличаются порядком расположения эл-тов, или хотя бы одним эл-том.
=
Сочетанием из n по m называется набор m элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
= =
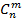Свойства сочетаний:
1. = 
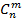2. + 
= 
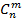3. 
= 
= 
= 1
4. 
+ 
+ 
+ …. + = 
Основные понятия теории вероятностей: испытания и события, виды случайных событий, классическое определение вероятности, примеры непосредственного вычисления вероятностей
Под событием в теории вероятности понимают то о чем имеет смысл говорить происходит оно или нет, при осуществлении определенной совокупности условий (испытание). Событие – результат (исход) испытания.
События делят на:
· достоверные (обязательно произойдут);
· невозможные (никогда не произойдут);
· случайные (или произойдет, или нет).
Случайные события зависят от множества случайных причин. Все их учесть невозможно, т.к. число и законы действия их неизвестны.
Виды случайных событий:
1. несовместные (появление одного исключает появление других);
2. единственно возможные (полная группа событий): события, появление одного из которых в результате испытания является достоверным (всё что возможно);
3. равновозможные: события, любое из которых по отношению к другим не обладает никаким преимуществом появиться чаще при многократных испытаниях в одинаковых условиях.
Вероятностью события А называется отношение числа исходов благоприятствующих событию А к общему числу единственно возможных и равно возможных элементарных исходов.
Р(А) = 
, где А – событие,
n – общее число исходов,
m – число исходов благоприятствующих событию,
Р – вероятность события А
Свойства вероятностей:
1. вероятность достоверного события (
) равна 1
Р() = 1
2. вероятность невозможного события (
) равна 0
Р() = 0
3. вероятность случайного события, есть положительное число между 0 и 1
0≤Р(А)≤1
Теорема сложения вероятностей несовместных событий: Р(А+В) = Р(А) + Р(В)
Полная группа событий если события А1, А2… Аn несовместны и их сумма достоверное событие, то А1, А2… Аn образуют полную группу событий (сумма вероятностей событий А1, А2,..., Аn, образующих полную группу, равна единице Р (A1) + Р (А2) +... + Р (Аn) = 1).
Противоположные события: два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать 
Теорема умножения вероятностей. Независимые и зависимые события.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В. Р(А 
В) = Р(А) Р(В)
Событие В называют зависимым от события А, если появление события А изменяет вероятность события В. Р(А+В) = Р(А) РА(В)
Вероятность появления хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 
. Р(А) = 1 – ().
Всем удачи на экзамене