Тема: Неравенства. Рациональные, иррациональные, логарифмические и тригонометрические неравенства
Определение 1. Неравенства, имеющие одно и то же множество решений, называют равносильными.
При решении неравенств обычно данное неравенство преобразуется в ему равносильное.
Определение 2. Область определения неравенства - это множество таких значений х, при которых имеют смысл обе части неравенства.
Мотивация. Неравенства сами по себе представляют интерес для изучения, т.к. именно с их помощью на символическом языке записываются важнейшие задачи познания реальной действительности. Часто неравенство служит важным вспомогательным средством, позволяющим доказать или опровергнуть существование каких-либо объектов, оценить их количество провести классификацию. Поэтому, с неравенствами приходится сталкиваться не менее часто, чем с уравнениями.
Иррациональными называются неравенства, в которых переменная содержится под знаком корня.
Иррациональное неравенство, как правило, сводится к равносильной системе (или совокупности систем) неравенств.
Рассмотрим примеры с решением иррациональных неравенств.
1. Решением данного неравенства 
<−9 является:
· x∈∅
· x∈(81;+∞)
· x∈R
· x∈(−∞;81)
Решение: Значением квадратного корня является неотрицательное число.
Поэтому значение выражения в левой части неравенства не может быть меньше −9, следовательно, данное неравенство решения не имеет.
x∈∅.
2. Решением данного неравенства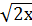 
+2≤5 является:
· x∈[0;4,5]
· x∈[0;+∞)
· x∈(0;4,5)
· x∈(−∞;4,5]
Решение: 1. Находим область определения неравенства. Выражение под знаком корня неотрицательное, поэтому оно должно быть больше или равно нулю:
Обл. опр. 2x≥0; x≥0.
Чертим ось x, на которой откладываем полученное значение закрашенной точкой, на что указывает знак неравенства в области определения. Закрашиваем тот интервал, который находится по правую сторону от отложенного значения.
x∈[0;+∞).
2. Решаем неравенство.
≤5−2; ≤3.
Так как обе части неравенства неотрицательные, то их можно возвести в квадрат, чтобы в левой части избавиться от знака корня.
2x≤9; x≤4,5.
Чертим ось x, на которой откладываем полученное значение закрашенной точкой, на что указывает знак неравенства. Закрашиваем тот интервал, который находится по левую сторону от отложенного значения.
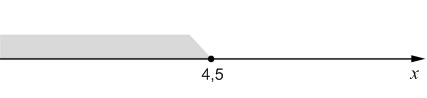
x∈(−∞;4,5].
3. Решением данного неравенства является пересечение полученного решения и области определения.
x∈[0;4,5].
3. Решением данного неравенства 
>3 является:
· x∈(−∞;−5]∪[5;+∞)
· x∈(−∞;−4]∪[4;+∞)
· x∈[−5;5]
· x∈(−∞;−5)∪(5;+∞)
· x∈(−∞;−4)∪(4;+∞)
· x∈(−5;5)
Решение: 1. Находим область определения. Выражение под знаком корня должно быть неотрицательным, т.е. больше или равно нулю.
Х2 −16≥0
Решаем квадратичное неравенство.
Приравниваем левую часть неравенства к нулю и находим корни.
X2−16=0
X2=16, x=±4
Графиком квадратичной функции является парабола. Чертим ось x, на которой откладываем полученные значения x закрашенными точками (на это указывает знак неравенства в области определения). Ветви параболы направлены вверх, так как коэффициент при x2 положительный. Закрашиваем положительные интервалы.
x∈(−∞;−4]∪[4;+∞)
2. Так как обе части неравенства неотрицательны, то их можем возводить в квадрат, чтобы избавиться от знака корня в левой части. Решаем неравенство.
>3
X2−16>9, x2−16−9>0, x2−25>0
X2−25=0, x2=25, x=±5
Графиком квадратичной функции является парабола. Чертим ось x, на которой откладываем полученные значения x незакрашенными точками (на что указывает знак данного неравенства). Ветви параболы направлены вверх, так как коэффициент при x2 положительный. Закрашиваем положительные интервалы.
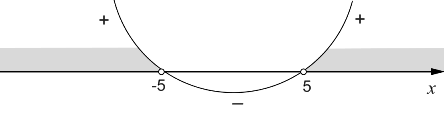
x∈(−∞;−5)∪(5;+∞)
3. Решением данного неравенства является пересечение полученного решения и области определения. 
x∈(−∞;−5)∪(5;+∞)
Решение логарифмического неравенства с основанием а 
Найди решение неравенства
log1/3(3x−4)<log1/3(x+3)
Решение:
Для решения данного неравенства, заметим, что в обеих частях неравенства даны логарифмы по одному и тому же основанию.
log1/3(3x−4)<log1/3(x+3)
Учитывая, что основанием логарифмов является число меньше 1, и используя теорему 6, составим систему неравенств, равносильную заданному логарифмическому неравенству:
3x−4>x+3
3x−4>0
x+3>0
Если выполняется третье неравенство системы, то автоматически выполняется и второе, значит, второе неравенство — следствие третьего и его можно отбросить. Получим:
{3x−4>x+3
x+3>0
Решая каждое неравенство, получим:
3x−4>x+3, 3x−x>3+4, 2x>7, x>7/2 и x+3>0, x>−3
Отметив найденные промежутки на одной координатной прямой, можно сделать вывод, что решением системы неравенств является промежуток, на котором обе штриховки совпали.
−3 7/2
Ответом будет открытый луч
x∈(7/2;+∞)