Средняя арифметическая. Средняя гармоническая

Вариант 10

Оглавление

 

Теоретические вопросы.. 3

Практические задания. 13

Библиографический список. 16

 

Теоретические вопросы

Сущность и значение средних величин. Виды средних величин. Правила выбора формы средней

 

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин.

Вычисление среднего - один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнори­рует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей.

Там, где возникает потребность обобщения, расчет таких характе­ристик приводит к замене множества различных индивидуальных зна­чений признака средним показателем, характеризующим всю совокуп­ность явлений, что позволяет выявить закономерности, присущие мас­совым общественным явлениям, незаметные в единичных явлениях.

Средняя отражает характерный, типичный, реальный уровень изу­чаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве.

Средняя - это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает.

 

Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется, одна из средних величин: арифметическая, гар­моническая, геометрическая, квадратическая, кубическая и т.д. Пере­численные средние относятся к классу степенных средних.

Помимо степенных средних в статистической практике использу­ются средние структурные, в качестве которых рассматриваются мода и медиана.

Остановимся подробнее на степенных средних.

Средняя арифметическая

Наиболее распространенным видом средних является средняя арифметическая. Она применяется в тех случаях, когда объем варьиру­ющего признака для всей совокупности является суммой значений при­знаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объяс­няется ее распространенность как обобщающего показателя, например: общий фонд заработной платы - это сумма заработных плат всех ра­ботников, валовый сбор урожая - сумма произведенной продукции со всей посевной площади.

Чтобы исчислить среднюю арифметическую, нужно сумму всех зна­чений признаков разделить на их число.

Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой служит про­стая средняя.

Средняя арифметическая простая равна простой сумме от­дельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):

,

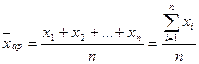где 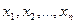- индивидуальные значения варьирующего (варианты); п - число единиц совокупности.

Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).

Средняя арифметическая взвешенная - средняя сгруппиро­ванных величин 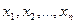, - вычисляется по формуле:

,

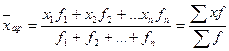где 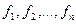- веса (частоты повторения одинаковых признаков);

- сумма произведений величины признаков на их частоты;

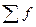- общая численность единиц совокупности.

Средняя гармоническая

Когда статистическая информация не содержит частот f по отдель­ным вариантам х совокупности, а представлена как их произведение 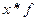, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим , откуда 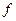= w/x. Теперь преобра­зуем формулу средней арифметической таким образом, чтобы по име­ющимся данным х и w можно было исчислить среднюю. В формулу средней арифметической взвешенной вместо xf подставим 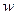вместо 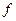- отношение w/x и получим формулу средней гармонической взвешенной:

.

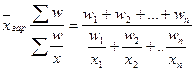Из формулы видно, что средняя гармоническая - средняя взвешенная из варьирующих обратных значений признака. Она являет­ся преобразованной формой арифметической средней и тождествен­на ей. Вместо гармонической всегда можно рассчитать среднюю ариф­метическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.

Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса 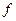, а известно w = xf, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины: .

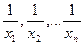В тех случаях, когда вес каждого варианта равен единице (индиви­дуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по форму­ле:

(

где - отдельные варианты обратного признака, встречающиеся по одному разу;

n – число вариантов.

Средняя геометрическая

Средняя геометрическая применяется в тех случаях, когда инди­видуальные значения признака представляют собой, как правило, отно­сительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динами­ки, т.е. характеризует средний коэффициент роста.

Средняя геометрическая исчисляется извлечением корня, сте­пени п из произведений отдельных значений - вариантов признака х:

,

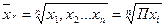где п - число вариантов;

П - знак произведения,

i = 1, 2, … п.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

Средняя квадратическая

В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или ку­бических единицах измерения. Тогда применяется средняя квадрати­ческая (например, для вычисления средней величины стороны п квад­ратных участков, средних диаметров труб, стволов и т.п.) и средняя куби­ческая (например, при определении средней длины стороны п кубов).

Средняя квадратическая простая является квадратным корнем из частного от делений суммы квадратов отдельных значений признака на их число:

Средняя квадратическая взвешенная рассчитывается по формуле:

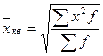
где 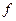- веса.

Соотношение для степенных средних может быть выражено сле­дующим образом:

,

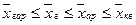Это соотношение называется правилом мажорантности средних.

Структурные средние

Структурные средние применяются для изучения внутреннего стро­ения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода (Мо) - значение случайной величины, встречающееся с наибольшей вероятностью, в дискретном вариационном ряду - вари­ант, имеющий наибольшую частоту.

В интервальных рядах распределения с равными интервалами, мода вычисляется по формуле:

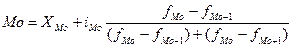
где 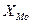- нижняя граница модального интервала;

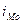- модальный интервал;

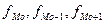- частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно). Модальный интервал определяется по наибольшей частоте.

Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.п.

Медиана (Me) - это вариант, который находится в середине ва­риационного ряда. Медиана делит ряд на две равные (по числу единиц) части - со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.

Номер медианы для нечетного объема вычисляется по формуле

,

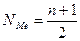где п - число членов ряда.

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признаках. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение меди­аны вычисляется линейной интерполяцией по формуле:

,

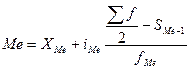где 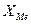- нижняя граница медианного интервала;

 

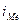- медианный интервал;

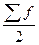- половина от общего числа наблюдений;

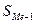- сумма наблюдений, накопленная до начала медианного ин­тервала;

- число наблюдений в медианном интервале. Формула (4.13) получена исходя из допущения о равномерности нарастания накоплений частоты внутри интервала и пригодна для лю­бого интервального ряда.

Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить асимметрию ряда распределения

Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.

 

Относительные статистические величины: понятие и виды. (относительная величина структуры, относительная величина координации, относительная величина интенсивности, относительная величина сравнения)

 

Относительный показатель в статистике - это обобщающий по­казатель, который представляет собой частное от деления одного аб­солютного показателя на другой и выражает соотношение между коли­чественными характеристиками изучаемых процессов и явлений.

Основные условия правильного расчета относительной величины - сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями.

Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения или основанием.

В зависимости от выбора базы сравнения относительный показатель может быть представлен в различных долях единицы: десятых;сотых (т.е. процентах - %) тысячных (десятая часть процента называется промилле - ‰); десятитысячных (сотая часть процента называется продецимилле – ⁰/₀₀₀)

Сопоставляемые величины могут быть как одноименными, так и раз­ноименными (в последнем случае их наименования образуются от наи­менований сравниваемых величин, например, руб./чел.; ц/га; руб./м²).

По своему содержанию относительные величины подразделяются на виды: относительные величины динамики, планового задания, выполнения планового задания, структуры, интенсивности, уровня экономического развития, координации и сравнения.

Относительными показателями структуры (ОПС) называются показатели, характеризующие долю отдельных частей изучаемой совокуп­ности во всем ее объеме. Они рассчитываются делением числа единиц (или объема явления) в отдельных частях совокупности на общее число единиц совокупности (или объем явления). Выражаются они простым кратным отношением или в процентах.

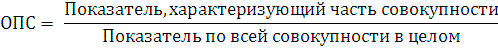
Относительными показателями интенсивности (ОПИ) называют показатели, характеризующие степень распространения или уровень раз­вития того или иного явления в определенной среде. Они вычисляются путем сравнения разноименных величин, находящихся в определенной связи между собой.

Эти показатели обычно определяются в расчете на 100, 1000 и т.д. единиц изучаемой совокупности (на 100 га земли, на 1000 человек на­селения и т.д.) и являются именованными числами. Примерами могут служить плотность населения, выражающаяся средним числом жите­лей на одном квадратном километре территории (8,6 чел./км² в Рос­сии в 1996 г.), обеспеченность населения медицинскими кадрами (чис­ленность врачей всех специальностей - 44,5 врача на 10 000 россиян на начало 1996 г.), возрастные коэффициенты рождаемости (число ро­дившихся в среднем за год на 1000 женщин по возрастным группам).

Разновидностью относительных величин интенсивности являются относительные показатели уровня экономического развития, характе­ризующие уровни ВВП, ВНП, НД и других показателей на душу населе­ния и играющие важную роль в оценке развития экономики страны.

Относительными показателями координации (ОПК) называют по­казатели, характеризующие соотношение отдельных частей целого между собой.

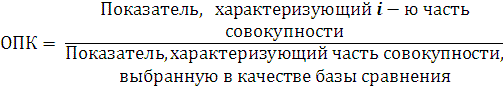
Вычисление этого вида показателей производится путем деления одной части целого на другую часть целого. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. Таким образом, относительные показатели координации являются разновидностью относительных показателей интенсивности, с той лишь разницей, что они показывают степень распространения, развития разнородных признаков одной и той же совокупности (целого). В зависимости от поставленной задачи тот или иной признак может быть принят за базу. Поэтому для одной и той же совокупности можно исчислить несколько относительных показателей координации.

Относительными показателями сравнения (ОПСр) называют показа­тели, представляющие собой частное от деления одноименных абсолютных статистических величин, характеризующих разные объекты (пред­приятия, фирмы, районы, области, страны и т.д.) и относящихся к одно­му и тому же периоду (или моменту) времени. Например, соотношение между уровнями себестоимости определенного вида продукции, вы­пущенной на двух предприятиях, между уровнями производительности труда в разных странах (при одинаковой методике счета).

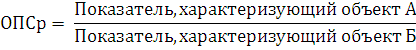
Рассчитывая относительные величины сравнения, следует обращать внимание на сопоставимость сравниваемых показателей с пози­ций методологии их исчисления, поскольку по целому ряду показателей методы их исчисления в разных странах или в разные периоды времени неодинаковы. Поэтому прежде чем рассчитывать относительные показатели сравнения, приходится решать задачу пересчета сравниваемых показателей по единой методологии.

 

Практические задания

 

1. Решить задачу:

Предприятие покупает сырье у двух поставщиков. Цены за тонну сырья составляют 3 тыс. руб. и 2,5 тыс. руб. В январе предприятие закупило у каждого поставщика сырье на сумму 120 тыс. руб. В феврале предприятие закупило сырье у первого поставщика на 90 тыс. руб., у второго на 170 тыс. руб.

Определите, как изменилась средняя цена за тонну сырья на предприятии.

Решение.

Логическая формула искомого показателя: Средняя цена 1 тонны = Стоимость закупки сырья / Количество закупленного сырья

Среднюю цену за тонну сырья на предприятии в каждом периоде определим по формуле средней гармонической взвешенной, т.к. в логической формуле неизвестен знаменатель .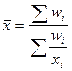

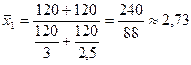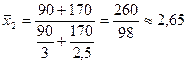руб.

руб.

Таким образом, средняя цена за тонну сырья в феврале по сравнению с январем снизилась на 2,65-2,73 = -0,08 руб. (8 коп.) или в относительном выражении на -2,9%.

 

2. Решить задачу:

Определить объем в тоннах условного мыла, если имеется 250 т мыла с содержанием жирных кислот 40% и 150 т с содержанием жирных кислот 60%.

Решение.

За базу сравнения примем мыло с содержанием жирных кислот 40%.

Тогда объем в тоннах условного мыла 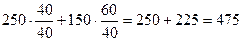т.

 

3. Решить задачу:

Имеются данные о стоимости продукции отрасли промышленности за 2007 – 2016 гг. (млрд. руб.).

17,1	23,2	29,7	31,3	33,3	30,4	30,6	27,5	36,4	32,8

Определить абсолютные, относительные, средние, цепные и базисные показатели ряда различными методами.

Решение.

Рассчитаем цепные и базисные абсолютные приросты, темпы роста и прироста; абсолютное значение 1 % прироста, а также средний уровень ряда, средние абсолютный прирост, темп роста и прироста.

Среднегодовые доходы населения за исследуемый период определим по формуле средней арифметической простой: 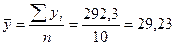млрд.руб.

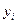Рассчитаем цепные абсолютные приросты динамического ряда, определяемые по формуле , где - текущий уровень ряда, 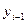- уровень, предшествующий .

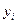Рассчитаем базисные абсолютные приросты динамического ряда, определяемые по формул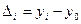е , где 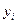- текущий уровень ряда, 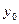- начальный уровень ряда.

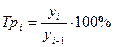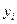Рассчитаем цепные темпы роста динамического ряда, определяемые по формуле , где - текущий уровень ряда, 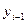- уровень, предшествующий .

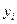Рассчитаем базисные темпы роста динамического ряда, определяемые по формул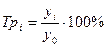е , где 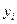- текущий уровень ряда, 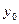- начальный уровень ряда.

Определим цепные темпы роста по формуле: .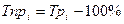

Определим базисные темпы роста по формуле: .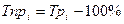

Абсолютное значение 1% прироста определяется по формул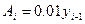е: , где 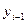- уровень, предшествующий .

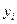Данные расчетов сведем в таблицу.

Год	Стоимость продукции, млрд.руб.	Абсолютные приросты, млрд.руб.	Темпы роста, %	Темпы прироста, %	Абсолютное значение 1% прироста, млрд.руб.
базисные	цепные	базисные	цепные	базисные	цепные
	17,1	-	-	100,0	-	-	-	-
	23,2	6,1	6,1	135,7	135,7	35,7	35,7	0,171
	29,7	12,6	6,5	173,7	128,0	73,7	28,0	0,232
	31,3	14,2	1,6	183,0	105,4	83,0	5,4	0,297
	33,3	16,2		194,7	106,4	94,7	6,4	0,313
	30,4	13,3	-2,9	177,8	91,3	77,8	-8,7	0,333
	30,6	13,5	0,2	178,9	100,7	78,9	0,7	0,304
	27,5	10,4	-3,1	160,8	89,9	60,8	-10,1	0,306
	36,4	19,3	8,9	212,9	132,4	112,9	32,4	0,275
	32,8	15,7	-3,6	191,8	90,1	91,8	-9,9	0,364

Определение среднего абсолютного прироста производится по цепным абсолютным приростам по формуле: 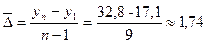млрд.руб.

Средний темп роста вычисляется по формуле средней гармонической .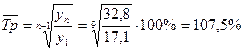

Средний темп прироста вычисляется по формуле: .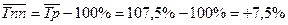

Библиографический список

 

1. Елисеева, И. И. Статистика: [углубленный курс]: учебник для бакалавров / И. И. Елисеева и др.]. – Москва: Юрайт: ИД Юрайт, 2016. – 565 с.

2. Теория статистики: Учебник/Под ред. проф. Г.Л. Громыко. — М.: ИНФРА-М, 2015. — 414 с. — (Серия «Высшее образование»)

3. Теория статистики: Учеб. пособие / Под ред. Р.А. Шмойловой- М.: Финансы и Статистика, 2016.

4. Экономическая статистика: Учебник /Под ред. Ю.Н. Иванова. – М.: ИНФРА-М, 2014. – 480 с.