Решение ОДУ первого порядка

Лабораторная работа №1

«Изучение интерфейса пакета моделирования Maple»

 

Цель и задачи работы.

Приобретение навыков работы с системой Maple

Теоретические сведения.

Долгое время системы Maple имели довольно архаичный (хотя и неплохой) пользовательский интерфейс, ориентированный на операционную систему MS-DOS. Но затем версия Maple V R3, далее Maple V R4, Maple V R5 и, наконец, Maple 6 приобрели вполне современный графический пользовательский интер­фейс, характерный для приложений операционных систем Windows 95/98/NT. Это намного повысило удобство работы с системой и обеспечило простую инте­грацию со многими другими программными продуктами.

Пользовательский интерфейс Maple 6 позволяет готовить документы в стиле Notebook (Блокнот), содержащие одновременно текстовые комментарии, зада­ния в виде функций в командной строке (с возможным преобразованием их в естественную математическую форму), результаты вычислений в виде обычных математических формул и графические данные. Это обеспечивает высокую сте­пень визуализации как исходных данных, так и результатов вычислений.

В основе пользовательского интерфейса Maple 6 лежит графический интерфейс операционной системы Windows 95/98/NT/2000. Интерфейс Maple 6 является многооконным. Управление системой возможно с помощью главного меню, па­нелей с кнопками быстрого управления и «горячих» клавиш. Реализуются мно­гие возможности графического манипулятора — мыши, присущие приложениям под Windows.

Важно отметить и прекрасно выполненную справочную систему Maple 6. Пре­одолев первые трудности общения с системой, пользователь быстро осваивает систему помощи, которая позволяет без какой-либо документации получить ис­черпывающую информацию о любом операторе, функции или пакете примене­ния системы (разумеется, на английском языке). В каждую справку входит по несколько примеров применения, причем их можно скопировать и перенести в редактор или в окно исполняемых документов системы. Это способствует быст­рому обучению пользователя.

Пользователь (как и в ряде других математических систем) работает с докумен­тами, которые являются одновременно описаниями алгоритмов решения задач, программами и результатами их исполнения. Они размещаются в соответствую-. щих ячейках. Графические построения выполняются как в ячейках документа, так и в отдельных окнах и имеют свои меню для оперативного управления па­раметрами графики.

После загрузки и запуска системы можно начать диалог с ней, используя ее опе­раторы и функции (с параметрами) для создания и вычисления математических выражений. На рис. 1.1 представлен реальный диалог с системой (в виде пря­мой копии с экрана) при решении простейших арифметических задач и построе­нии графика функции sin(.r)/x.

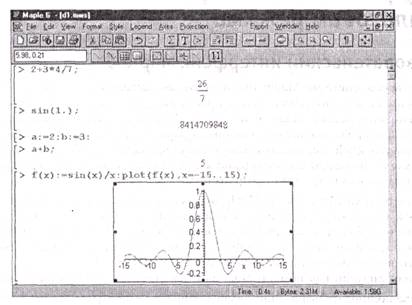
Рис. 1.1. Начало диалога с системой Maple 6

Уже из этого простого примера видны особенности диалога с системой и син­таксиса ее входного языка, то есть языка задания системе вопросов. Диалог идет в стиле «задал вопрос, получил ответ». Вопросы и ответы занимают отдельные блоки, выделяемые в левой части квадратными скобками. Длина квадратных скобок зависит от размера выражений — исходных (вопроса) и результатов вы­числений (ответов на вопросы). Знак > является знаком приглашения к зада­нию вопроса. Мигающая вертикальная черта | — маркер ввода.

Ввод выражений (вопросов) задается по правилам, давно принятым для строч­ных редакторов. Они хорошо известны, и мы не будем на них останавливаться подробно. Отметим лишь, что клавиша Ins позволяет задавать два основных ре­жима ввода — замены и вставки. В режиме замены вводимый символ заменяет существующий символ, который отмечен маркером ввода. А в режиме вставки новый символ вставляется в текст, не уничтожая имеющиеся символы.

Перемещение маркера ввода осуществляется клавишами <- и -» перемещения курсора. Клавиша Backspace стирает символ слева от маркера ввода, а клави­ша Del — справа от маркера ввода. Для ввода любого символа надо нажать соот­ветствующую клавишу. Клавиша Shift включает верхний регистр для ввода больших (заглавных) букв, а клавиша Caps Lock переключает верхний и нижний регистры (они меняются местами).

Знак фиксации конца выражения; (точка с запятой) указывает, что результат его вычисления должен быть выведен на экран дисплея, а знак: (двоеточие) отменяет вывод и может использоваться как знак разделителя при записи не­скольких выражений в одной строке. Клавиши перемещения курсора позволяют пробежаться по ранее введенным строкам сеанса (сессии) работы.

Важным понятием системы Maple 6 (да и математики вообще) является поня­тие функции. Функция возвращает результат некоторого преобразования ис­ходных данных — параметров функции. Maple 6 имеет множество встроенных функций, хранящихся в его ядре и пакетах расширения.

Функция в выражениях вводится заданием ее имени и списка из одного или не­скольких параметров в круглых скобках — например, sqrt (2) задает функцию вычисления квадратного корня с параметром 2 (численной константой). Основ­ным признаком функции является возврат значения в ответ на обращение к функции по ее имени (идентификатору) с указанием списка параметров функ­ции. Например:

Обратите внимание на особую роль десятичной точки — здесь она служит ука­занием о вычислении значения sin(l.O) или, что то же самое, sin(l.). А вот синус для целочисленного аргумента 1 не вычисляется — считается, что вычисленное значение менее ценно, чем значение sin(l).

Ради единства терминологии мы будем пользоваться расширительным поняти­ем функции, относя к нему и те объекты, которые в обычных языках програм­мирования именуют процедурами или командами. Например, графические объ­екты plot и plot3d мы также будем считать функциями, возвращающими графики. Под командами мы будем подразумевать такие указания системе, ко­торые готовят ее к определенным действиям, но сами по себе эти действия не выполняют. К командам относятся также действия по изменению интерфейса и выполнению операций с файлами. Словом, команды — это действия, не связан­ные с возвратом чего-либо.

Помимо функций в математических системах для записи математических выра­жений используются специальные знаки — операторы. К примеру, вычисление квадратного корня часто записывается с помощью его специального знака — V. Достаточно хорошо известны операторы сложения +, вычитания -, умноже­ния *, деления / и некоторые другие. Операторы обычно используются с опе­рандами в виде констант или переменных, например, в записи 2* (3+4) числа 2, 3 и 4 — это операнды, а знаки * и + — операторы. Скобки используются для изменения порядка выполнения операций. Так, без них 2*3+4=10, тогда как 2* (3+4) =14, поскольку вначале вычисляется выражение в скобках.

Пожалуй, самым распространенным оператором является оператор присваива­ния: =. Он используется для задания переменным конкретных значений, на­пример:

Этот простой пример наглядно иллюстрирует эволюцию переменных и особую роль оператора присваивания в системе Maple V. В частности, в этом примере переменные х, у и z взаимосвязаны с помощью операций присваивания. Поэто­му задание значения числа 2 последней переменной приводит к тому, что и пе­ременные у и х принимают то же значение.

Другой распространенный оператор равенства = используется для задания ра­венств и логических условий (например, а=Ь), указания областей изменения переменных (например, i=l.. 5 означает формирование диапазона изменения i от 1 до 5) и значений параметров-опций в функциях и командах (например, color=black для задания черного цвета у линий графиков).

Операторы сами по себе результат не возвращают. Но они наряду с функциями и своими параметрами (операндами), позволяют конструировать математические выражения, которые при их вычислении также возвращают результат. В силу этого математические выражения, содержащие операторы и операнды, могут быть параметрами функций. Выражения в Maple V бывают очень простыми (напри­мер, имена переменных х и у или константы 1 и 2), а могут содержать многие тысячи знаков.

С позиции канонов символьной математики квадратный корень из двух уже яв­ляется основным результатом вычислений. Поэтому такая функция обычно не вычисляется в численном виде, а выводится в естественном виде, с примене­нием знака квадратного корня V. Для вычисления в привычном виде (в виде десятичного числа с мантиссой и порядком) надо воспользоваться функцией evalf (sqrt (2)) — эта функция обеспечивает вычисление символьного выра­жения, заданного ее параметром (числом 2).

На рис. 1.1 показано, как задается функция пользователя f (х) с одним пара­метром х. Нетрудно заметить, что параметр указывается в скобках после имени функции, а для записи выражения функции используется знак присваивания: = (двоеточие со знаком равенства). Для построения графика функции f (x) исполь­зуется функция plot в форме

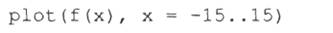
Нетрудно заметить, что при наличии нескольких параметров функции (в нашем случае их два) они разделяются запятыми. Выражение х=-15..15 задает, во-первых, указание, относительно какой переменной строится график, а во-вто­рых, говорит, в какой области значений меняются значения этой переменной — в нашем случае от -15 до +15. Шаг изменения переменной выбирается автома­тически, чтобы график был достаточно представительным.

Столь же просто, как и график обычной функции в декартовой системе коорди­нат, можно построить график трехмерной поверхности. Это показано на примере рис. 1.2. В данном случае задана функция двух переменных Z (х, у):=sin(x*y), и ее график строится с использованием графической функции plot 3d. Правила задания пределов изменения переменных х и у соответствуют описанным выше.

 

 

Рис. 1.2. Построение графика трехмерной поверхности

Задание на работу.

- изучить теоретическую часть;

- смоделировать заданную преподавателем функцию и получить ее график.

Содержание отчета.

Программа моделирования и ее результаты

 

Лабораторная работа №2

«Интерполяция, экстраполяция и аппроксимация в среде Maple»

Цель и задачи работы.

Изучение методов интерполяции, экстраполяции и аппроксимации в среде Maple

Теоретические сведения.

Если некоторая зависимость у(х) представлена рядом табличных отсчетов //;(*,), то интерполяцией принято называть вычисление значений у{х) при заданном х, расположенном в интервале между отсчетами. За пределами общего интервала определения функции [а, Ь], то есть при х < а и х > b вычисление у(х) называют экстраполяцией (или, иногда, предсказанием значений функции). В данном слу­чае речь идет об одномерной интерполяции, но возможны двумерная интерпо­ляция функций двух переменных z(x, у) и даже многомерная интерполяция для функций многих переменных.

Интерполяция и экстраполяция часто выполняются по некоторой скрытой, но подразумеваемой зависимости. Например, если узловые точки функции соеди­нить отрезками прямых, то будем иметь многоинтервальную линейную интер­поляцию данных. Если использовать отрезки параболы, то интерполяция будет параболической. Особое значение имеет многоинтервальная сплайн-интерполя­ция, области применения которой уже сейчас весьма обширны и непрерывно расширяются. Интерполяция рядом Фурье (набором синусоидальных функ­ций) также достаточно хорошо известна; она эффективна при интерполяции пе­риодических функций.

Аппроксимацией в системах компьютерной математики обычно называют полу­чение приближенных значений какого-либо выражения. Однако под аппрокси­мацией функций подразумевается получение некоторой конкретной функции, вычисленные значения которой с некоторой точностью аналогичны аппрокси­мируемой зависимости. Обычно предпочитают найти одну зависимость, прибли­жающую заданный ряд узловых точек. Часто для этого используют степенные многочлены — полиномы.

Здесь мы будем рассматривать такие виды аппроксимации, которые дают точ­ные значения функции у(х) в узловых точках в пределах погрешности вычисле­ний по умолчанию. Если аппроксимирующая зависимость выбирается из усло­вия наименьшей среднеквадратической погрешности в узловых точках (метод наименьших квадратов), то мы имеем регрессию или приближение функций по методу наименьших квадратов.

Если функция задана аналитически, то наиболее простым способом нахождения ее аппроксимирующей зависимости является применение функции convert. Это поясняют следующие примеры:

На рис. 2.1 представлен пример полиномиальной аппроксимации хорошо из­вестной статистической функции erf с (х). Для полинома задана максимальная степень 12, но ввиду отсутствия в разложении четных степеней максимальная степень результата оказывается равна 11.

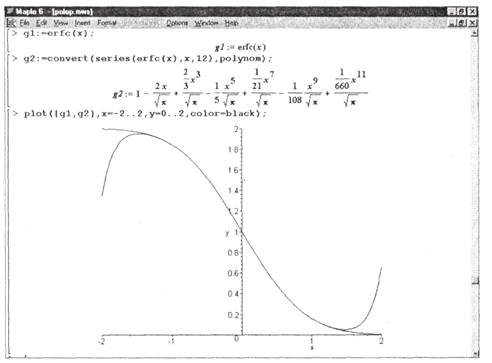
Рис. 2.1. Пример полиномиальной аппроксимации функции erfc(x)

Как видно из приведенного рисунка, в интервале изменения.г от -1,5 до 1,5 ап­проксимирующее выражение почти повторяет исходную зависимость. Однако затем график аппроксимирующей функции быстро отходит от графика исход­ной зависимости. При этом он ведет себя иначе даже качественно, никоим обра­зом не показывая асимптотическое поведение, характерное для исходной зави­симости.

Если данные некоторой зависимости у(х) заданы векторами X и Y ее дискрет­ных значений, то для получения интерполяционного степенного многочлена достаточно записать многочлен для всех iVnap значений г/,(х,) при i = 1...N (или i = 0... N - 1, если индексы отсчетов начинаются с нуля). Полученная при этом система линейных (относительно коэффициентов полинома) уравнений после решения дает коэффициенты аппроксимирующего полинома. Степень полино-1 ма на 1 меньше N, а вычисляемые при х, значения г/, (х,) совпадают с табличны­ми (узловыми) в пределах вычислительной погрешности.

На самом деле все это делать не нужно, поскольку Maple 6 имеет реализующую данный алгоритм встроенную функцию interp (X, Y, v) или, в инертной фор­ме, Interp(X,Y, v).

Переменная v указывает имя переменной интерполяционного полинома. Векто­ры X и Y должны содержать п + 1 = N координат точек исходной зависимости, где п — степень интерполирующего полинома.

Рисунок 2.2 показывает технику применения полиномиальной аппроксимации на основе функции interp с построением графика исходных точек и аппрокси­мирующего полинома. Нетрудно заметить, что график полинома проходит точ­но через исходные точки — они даны квадратиками.

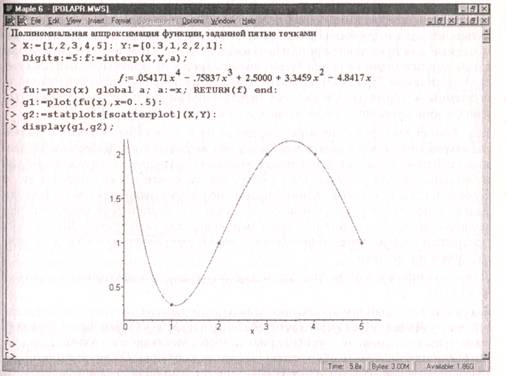
Рис. 2.2. Пример осуществления полиномиальной аппроксимации

В этом примере полезно присмотреться к визуализации результатов вычисле­ний и совместному построению графика интерполирующего полинома и исход­ных точек. В частности, для построения последних использованы средства паке­та stats, позволяющие выводить на график точки с заданными координатами, причем не только в виде точек, но и в виде маленьких крестиков, кружков, квад­ратов и других фигур. Для выбора типа точек и других параметров графика его надо выделить (установив указатель мыши в поле графика и щелкнув левой кнопкой) и нажать правую кнопку мыши — появится контекстно-зависимое меню с операциями форматирования графика.

Приведем еще несколько примеров использования функции Interp.

Точность полиномиальной интерполяции катастрофически падает при увеличе­нии степени аппроксимирующих полиномов. От этого недостатка можно изба­виться, используя для интерполяции отрезки полиномов невысокой степени, при­меняемые для представления части узловых точек. Самым известным методом такой интерполяции является сплайн-интерполяция на основе отрезков кубиче­ских полиномов. При этом аппарат сплайн-интерполяции позволяет получить полиномы, которые дают в узловых точках непрерывность не только представ­ляемой ими функции, но и ее первых и даже вторых производных.

Наглядно сплайн-функцию можно представить в виде гибкой стальной линей­ки, закрепленной в узловых точках и плавно изгибающейся. Благодаря указан­ным свойствам сплайнов они неплохо описывают функции, представленные как небольшим числом узловых точек (благодаря плавности сплайн-кривых), так и функции, представляемые очень большим числом узловых точек (поскольку по­рядок полиномов от этого числа уже не зависит). Недостатком сплайн-интер­поляции является отсутствие общего выражения для всей кривой. Фактически приходится использовать набор сплайн-функций для различных интервалов меж­ду узловыми точками.

Для получения сплайн-интерполяции используется Maple-функция spline (X, Y,var,d).

Здесь х и Y — одномерные векторы одинакового размера, несущие значения ко­ординат узловых точек исходной функции (причем в произвольном порядке), var — имя переменной, относительно которой вычисляется сплайн-функция, наконец, необязательный параметр d задает вид сплайна. Он может иметь сле­дующие значения: linear — линейная функция, или полином первого порядка. quadratic — квадратичная функция, или полином второго порядка, cubic —полином третьего порядка, quartiс — полином четвертого порядка. Если пара­метр d опущен, то сплайн-функция будет строиться на основе полиномов третьего порядка (кубические сплайны).

Технику сплайновой интерполяции наглядно поясняет рис. 2.3. На нем пред­ставлено задание векторов узловых точек X и Y и четырех сплайиовых функций, по которым построены их графики. Для одной из сплайн-функций (с линейной интерполяцией между узлами) показано также полученное аналитическое выра­жение.

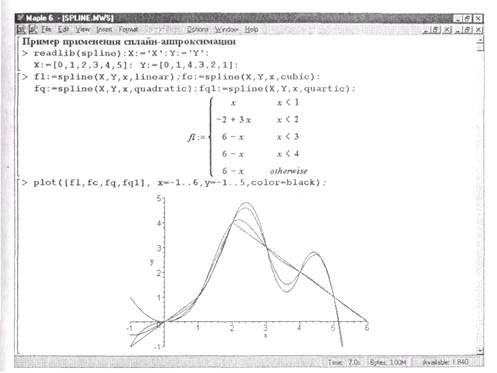
Рис. 2.3. Задание сплайновой интерполяции и построение графиков полученных функций

Как видно из рис. 2.3, сплайновая функция представляет собой кусочную функ­цию, определяемую на отдельных интервалах. При этом на каждом участке такая функция описывается отдельным полиномом соответствующей степени. Функция plot «понимает» такие функции и позволяет без преобразования ти­пов данных строить их графики. Для работы с кусочными функциями можно использовать функции convert и piecewise.

Задание на работу.

- изучить теоретическую часть;

- смоделировать заданную преподавателем функцию и получить ее график.

Содержание отчета.

 

Программа моделирования и ее результаты

 

Лабораторная работа №3

«Решение дифференциальных уравнений в среде Maple»

Цель и задачи работы.

Приобретение навыков решения диф. уравнений

Теоретические сведения.

Важное место в математических расчетах занимает решение дифференциальных уравнений. К нему, в частности, обычно относится анализ поведения различных систем во времени (анализ динамики), а также вычисление различных полей (тяготения, электрических зарядов и т. д.). Трудно переоценить роль дифферен­циальных уравнений в моделировании физических и технических объектов и систем. Maple 6 позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде. Поэтому данный урок целиком посвящен решению уравнений данного класса.

Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в разных формах записи:

Здесь ODE — одно обыкновенное дифференциальное уравнение или система из дифференциальных уравнений первого порядка с указанием начальных условий, у(х) — функция одной переменной, ICs — выражение, задающее начальные условия, {sysODE} — множество дифференциальных уравнений, {funcs} — множество неопределенных функций, extra_argument — опция, задающая тип решения.

Параметр extra_argument задает класс решаемых уравнений. Отметим основ­ные значения этого параметра:

О exact — аналитическое решение (принято по умолчанию);

О explicit — решение в явном виде;

О system — решение системы дифференциальных уравнений;

О ICs — решение системы дифференциальных уравнений с заданными началь­ными условиями;

О formal series — решение в форме степенного многочлена;

О integral transform — решение на основе интегральных преобразований Лапласа, Фурье и др.;

О series — решение в виде ряда с порядком, указываемым значением пере­менной Order;

О numeric — решение в численном виде.

Для решения задачи Коши в параметры dsolve надо включать начальные усло­вия, а при решении краевых задач — краевые условия. Если Maple способен найти решение при числе начальных или краевых условий меньше порядка сис­темы, то в решении будут появляться неопределенные константы вида _С1, __С2 _и т. д. Они же могут быть при аналитическом решении системы, когда началь-_ные условия не заданы. Если решение найдено в неявном виде, то в нем появится параметр Т. По умолчанию функция dsolve автоматически выбирает наибо­лее подходящий метод решения дифференциальных уравнений. Однако в пара­метрах функции dsolve d квадратных скобках можно указать предпочтитель­ный метод решения дифференциальных уравнений. Допустимы следующие методы:

Информацию о каждом методе можно получить, используя команду?dsolve, method. Например, команда?dsolve, linear вызовет появление страницы справочной системы с подробным описанием линейного метода решения диф­ференциальных уравнений.

Производные при записи дифференциальных уравнений могут задаваться функцией dif f или оператором D. Выражение sysODE должно иметь структуру мно­жества и содержать помимо самой системы уравнений их начальные условия.

Решение ОДУ первого порядка

Начнем рассмотрение практических примеров с решения одиночных обыкно­венных дифференциальных уравнений (ОДУ) первого порядка:

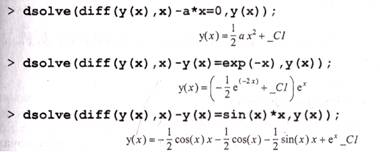
Следующие примеры иллюстрируют возможность решения одного и того же дифференциального уравнения ode_L разными методами: